2018-2019 ICPC Northwestern European Regional Programming Contest (NWERC 2018)

目录

• Contest Info
• Solutions
  • A. Access Points
  • B. Brexit Negotiations
  • E. Equality Control
  • G. Game Design
  • H. Hard Drive
  • I. Inflation
  • J. Jinxed Betting
  • K. Kleptography

Contest Info

---

传送门

Solved	A	B	C	D	E	F	G	H	I	J	K
8 / 11	Ø	O	-	-	Ø	-	Ø	O	O	Ø	O

• O 在比赛中通过
• Ø 赛后通过
• ! 尝试了但是失败了
• - 没有尝试

Solutions

---

A. Access Points

题意：
二维平面中给定(n)个点((x_i,y_i))。
现在要在二维平面中构造(n)个点，其中第(i)个点与((x_i,y_i))相连，构造的点可以重合，贡献为边权的平方。假设构造的第(i)个点为((X_i,Y_i))，那么对于(i<j,X_ileq X_j,Y_ileq Y_j)。
问最后最小的贡献为多少。

思路：

• 一条边的贡献为((x_i-X_i)^2+(y_i-Y_i)^2)，显然(x,y)独立，所以我们可以转化为两个一维问题。
• 问题转化为：数轴上给定(n)个点，现在要从小到大依次确定一个点，使得对应的贡献最小。
• 考虑(sum(x_i-a)^2)取最小值时，(a=average(x_i))，现在问题是(sum(x_i-a_i)^2)最小，直接将(x)分为尽可能多的连续的若干段，每一段取平均值即可。
• 实现的过程可以用一个栈来模拟。

其实就是经典的一个idea的变形，但可以把序列变为连续的若干段，这样问题就变为经典题目了。
详见代码：

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/6/10 14:55:43
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#include <stack>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
 
void run() {
    int n; cin >> n;
    vector <int> x(n), y(n);
    for (int i = 0; i < n; i++) {
        cin >> x[i] >> y[i];
    }
    
    auto gao = [&] (vector <int>& a) {
        stack <pair <ll, int>> s;
        for (int i = 0; i < n; i++) {
            pair <ll, int> now = MP(a[i], 1);
            while (!s.empty() && s.top().fi * now.se > now.fi * s.top().se) {
                pair <ll, int> t = s.top(); s.pop();
                now.fi += t.fi;
                now.se += t.se;
            }
            s.push(now);
        }
        double res = 0.0;
        int id = n - 1;
        while (!s.empty()) {
            pair <ll, int> t = s.top(); s.pop();
            double ave = 1.0 * t.fi / t.se;
            for (int i = id; i > id - t.se; i--) {
                res += (a[i] - ave) * (a[i] - ave);
            }
            id -= t.se;
        }
        return res;
    };
    
    double ans = 0.0;
    ans += gao(x);
    ans += gao(y);
    cout << ans << '
';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    run();
    return 0;
}

B. Brexit Negotiations

拓扑序+贪心。
从前往后贪心正确性得不到保障，但是从后往前即可解决这一问题。
很有意思，拓扑序有时候反着来就能解决很多问题QAQ。
代码写着较为复杂。。

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef long double ld;
const int MAXN = 4e5 + 5, MAXM = 4e5 + 5, BOUND = 2e5, MOD = 1e9+7, INF = 0x3f3f3f3f, base = 10000;
const int inv2 = (MOD + 1) >> 1;
const ll INFL = 0x3f3f3f3f3f3f3f3f;
const double PI = acos(-1.0), eps = 1e-9;
#define lson o<<1,l,m
#define rson o<<1|1,m+1,r
#define lc(x) ch[x][0]
#define pii pair<int,int>
#define vi vector<int>
#define vii vector<pair<int,int>>
#define rc(x) ch[x][1]
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define all(a) (a).begin(), (a).end()
#define sz(a) int(a.size())
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define fi first
#define se second
#define MP std::make_pair
#define ri register int
//#define sz(a) int((a).size())
const int N = 2e5,M = (1<<20);
inline int add(int a, int b) {return a + b >= MOD ? a + b - MOD : a + b;}
inline int dec(int a, int b) {return a < b ? a - b + MOD : a - b;}
inline int mul(int a, int b) {return 1ll * a * b % MOD;}
template <typename T>
inline void cmin(T &a,T b){a = min(a,b);}
template <typename T>
inline void cmax(T &a,T b){a = max(a,b);}
ll qpow(ll a,ll b){
    ll ans=1;
    for(;b;b>>=1,a=a*a%MOD)if(b&1)ans=ans*a%MOD;
    return ans;
}
mt19937 mrand(random_device{}());
int a[MAXN],f[MAXN],in[MAXN];
struct cmp{
    bool operator ()(int u,int v){
        return f[u] < f[v];
    }
};
vi G[MAXN];
bool vis[MAXN];
void dfs(int u){
    vis[u] = 1;
    f[u] = a[u];
    for(int v:G[u]){
        if(!vis[v])dfs(v);
        f[u] = max(f[u], f[v]+1);
    }
}
void run(){
    int n; cin>>n;
    rep(i,1,n){
        cin>>a[i];
        int x; cin>>x;
        rep(j,1,x){
            int u; cin>>u;
            G[u].push_back(i);
            in[i]++;
        }
    }
    rep(i,1,n){
        if(!vis[i]){
            dfs(i);
        }
    }
    priority_queue<int,vector<int>, cmp> q;
    rep(i,1,n)if(!in[i])q.push(i);
    int ans=0,cnt=0;
    while(!q.empty()){
        int u = q.top();q.pop();
        ans = max(ans, cnt + a[u]);
        for(int v:G[u]){
            if((--in[v])==0){
                q.push(v);
            }
        }
        cnt++;
    }
    cout<<ans<<'
';
}
int main() {
    ios::sync_with_stdio(false); cin.tie(0);
    //freopen("A.in","r",stdin);
    //freopen("A.out","w",stdout);
    int _=1;
    while(_--)run();
    return 0;
}

E. Equality Control

题意：
给定两个表达式，每个表达式有"combine","sorted","shuffle","[]"这四种运算符。其中"[]"中间有一个序列，形如(x_1,x_2,cdots,x_i)。
现在问这两个表达式是否等价。表达式等价的定义为出现每一种序列的概率都相同。

思路：
首先有几个观察：

• 形如shuffle[1,1,1,1]这种相当于没有进行操作；
• 无视combine操作；
• 表达式树中，如果某个结点出现了sorted或者shuffle，那么其叶子结点都没用了，最后只取决于它。

根据这三点很容易看两个表达式最后是否相等了，但是题目要求出现的概率相等。
那么再加一个条件，在满足数列相等后，所有shuffle的区间都相等就行（此时概率肯定相等）。如果存在一个区间不相等，那么最后两个式子肯定不等价。
详见代码：

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/6/9 23:22:06
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
 
typedef pair <vector <int>, vector<pii>> result;
 
result get(string& s) {
    int n = s.length();
    vector <int> a, sum(n, -1);
    for (int i = 0, j; i < n; i = j + 1) {
        j = i;
        if (s[i] >= '0' && s[i] <= '9') {
            int x = 0;
            while (j < n && s[j] >= '0' && s[j] <= '9') {
                x = x * 10 + (s[j] - '0');
                ++j;
            }
            sum[j - 1] = sz(a);
            a.push_back(x);
        }
    }
    vector <pii> seg;
    for (int i = 0, j; i < n; i = j + 1) {
        j = i;
        if (s[i] != 's') continue;
        int cnt = 0;
        while (j < n && (s[j] < '0' || s[j] > '9')) {
            if (s[j] == '(') ++cnt;
            ++j;
        }
        int L = INF, R = -1;
        while (j < n && cnt > 0) {
            if (s[j] == '(') ++cnt;
            if (s[j] == ')') --cnt;
            if (sum[j] != -1) {
                L = min(L, sum[j]);
                R = max(R, sum[j]);
            }
            ++j;
        }
        if (L > R) continue;
        sort(a.begin() + L, a.begin() + R + 1);
        if (s[i + 1] == 'h' && a[L] != a[R]) {
            seg.push_back(MP(L, R));
        }
    }
    return MP(a, seg);
}
 
void run() {
    string s, t; cin >> s >> t;
    result A = get(s), B = get(t);
    if (A == B) {
        cout << "equal" << '
';
    } else {
        cout << "not equal" << '
';
    }
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    run();
    return 0;
}

G. Game Design

题意：
给定一些操作符"LRUD"，表示往某一个方向走直到遇到障碍。
现在给定终点((0,0))，要求构造一个起点以及若干障碍物，使得最后小球能够到达终点。注意必须是最后一步到达终点，中间到达终点即不合法。
大概图就是这个样子：

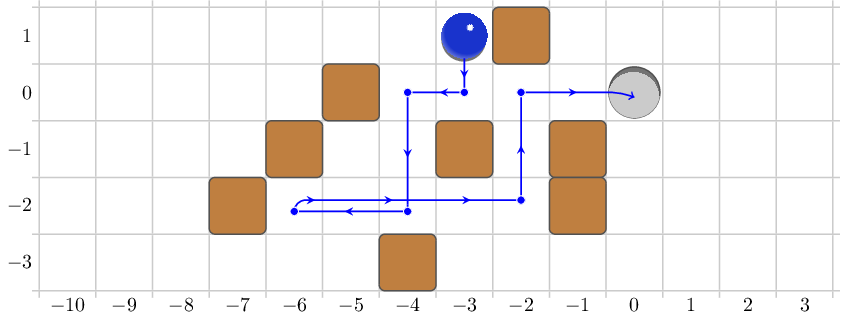
思路：
一般这种题都会考虑从后往前构造，但这个题中从后往前构造可能会很麻烦。
注意到我们终点的具体位置不重要，假设我们最后到达了某个点((x,y))，直接将坐标轴相对于((x,y))平移即可。
所以问题就转化为了从((0,0))出发，构造一种方案，使得存在一种合法的路径。
到了这一步就比较简单了。网格图中的移动一般是规定一个范围，每一次范围会变大或减小。因为这个题从((0,0))开始走，所以我们不断将范围变大并且每次走到边界即可，只要保证小球不会在路径上碰到障碍物就行。
注意特殊情况：LRL,RLR,UDU,DUD出现在了末尾则肯定不合法，若中间为LRLRLR这种则不扩大范围。
细节见代码：

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/6/9 15:25:32
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 20 + 5;
 
int n;
string s;
int d;
 
map <int, map<int, int>> mp;
 
void sayNo() {
    cout << "impossible" << '
';
    exit(0);   
}
 
void run() {
    cin >> s;
    n = s.length();
    if (n >= 3 && s[n - 1] == s[n - 3]) {
        if (s[n - 1] == 'L' && s[n - 2] == 'R') sayNo();
        if (s[n - 1] == 'R' && s[n - 2] == 'L') sayNo();
        if (s[n - 1] == 'U' && s[n - 2] == 'D') sayNo();
        if (s[n - 1] == 'D' && s[n - 2] == 'U') sayNo();
    }
    d = 1;
    int x = 0, y = 0;
    vector <pii> ans;
    for (int i = 0; i < n; i++) {
        if (s[i] == 'R') {
            x = d;
            ans.push_back(MP(x + 1, y));
        }
        if (s[i] == 'L') {
            x = -d;
            ans.push_back(MP(x - 1, y));
        }
        if (s[i] == 'D') {
            y = -d;
            ans.push_back(MP(x, y - 1));
        }
        if (s[i] == 'U') {
            y = d;
            ans.push_back(MP(x, y + 1));
        }
        if (i + 1 < n) {
            if (s[i] == 'L' && s[i + 1] == 'R') {}
            else if (s[i] == 'R' && s[i + 1] == 'L') {}
            else if (s[i] == 'U' && s[i + 1] == 'D') {}
            else if (s[i] == 'D' && s[i + 1] == 'U') {}
            else d += 2;
        }
    }
    
    cout << -x << ' ' << -y << '
';
    sort(all(ans));
    ans.erase(unique(all(ans)), ans.end());
    cout << sz(ans) << '
';
    for (auto it : ans) {
        cout << it.fi - x << ' ' << it.se - y << '
';
    }
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    run();
    return 0;
}

H. Hard Drive

贪心一下就行。
从后往前插入(1)，我们首先想让他贡献(2)次，如果是偶数就很简单，奇数会多一次我们插在(1)位置即可。

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/6/9 13:31:53
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
 
void run() {
    int n, c, b;
    cin >> n >> c >> b;
    vector <int> a(n, -1);
    for (int i = 0; i < b; i++) {
        int x; cin >> x; --x;
        a[x] = 0;
    }
    int t = c / 2;
    for (int i = n - 2; i >= 0 && t; i--) {
        if (a[i] == -1) {
            a[i] = 1;
            --t; --i;
        }
    }
    if (c & 1) {
        a[0] = 1;
    }
    for (int i = 0; i < n; i++) {
        if (a[i] == -1) a[i] = 0;
        cout << a[i];   
    }
    cout << '
';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    run();
    return 0;
}

I. Inflation

签到。

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef long double ld;
const int MAXN = 2e5 + 5, MAXM = 4e5 + 5, BOUND = 2e5, MOD = 1e9+7, INF = 0x3f3f3f3f, base = 10000;
const int inv2 = (MOD + 1) >> 1;
const ll INFL = 0x3f3f3f3f3f3f3f3f;
const double PI = acos(-1.0), eps = 1e-9;
#define lson o<<1,l,m
#define rson o<<1|1,m+1,r
#define lc(x) ch[x][0]
#define pii pair<int,int>
#define vi vector<int>
#define vii vector<pair<int,int>>
#define rc(x) ch[x][1]
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define all(a) (a).begin(), (a).end()
#define sz(a) int(a.size())
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define fi first
#define se second
#define MP std::make_pair
#define ri register int
//#define sz(a) int((a).size())
const int N = 2e5,M = (1<<20);
inline int add(int a, int b) {return a + b >= MOD ? a + b - MOD : a + b;}
inline int dec(int a, int b) {return a < b ? a - b + MOD : a - b;}
inline int mul(int a, int b) {return 1ll * a * b % MOD;}
template <typename T>
inline void cmin(T &a,T b){a = min(a,b);}
template <typename T>
inline void cmax(T &a,T b){a = max(a,b);}
ll qpow(ll a,ll b){
    ll ans=1;
    for(;b;b>>=1,a=a*a%MOD)if(b&1)ans=ans*a%MOD;
    return ans;
}
mt19937 mrand(random_device{}());
int c[MAXN];
void run(){
    int n; cin>>n;
    rep(i,1,n)cin>>c[i];
    sort(c+1,c+1+n);
    db frac = 1;
    rep(i,1,n){
        if(c[i]>i){
            cout<<"-1
";
            return ;
        }
        frac = min(frac,(db)c[i]/i);
    }
    printf("%.6f
",frac);
}
int main() {
    //ios::sync_with_stdio(false); cin.tie(0);
    int _=1;
    while(_--)run();
    return 0;
}

J. Jinxed Betting

假设当前除开第一个人其余分数最大值为(MAX)，有(cnt)个。并且现在最大和次大的差值为(d)。
显然模拟一下会发现经过(log_2lfloorfrac{cnt}{2} floor)次过后(MAX)会加一，并且再经过一次(d)会减少(1)。
也就是一个过程我们可以看作(log_2lfloorfrac{cnt}{2} floor+1)步，对于每一个值来说会重复(d)次，之后会更新(MAX,cnt)并且继续执行以上操作直到(MAX)超过(a[0])。
那么手动模拟一下这个过程即可，注意一下边界的情况。

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/6/9 22:17:52
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
 
void run() {
    int n; cin >> n;
    vector <ll> a(n);
    vector <int> lg(N);
    lg[2] = 1;
    for (int i = 3; i < N; i++) {
        lg[i] = lg[i >> 1] + 1;
    }
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    sort(all(a));
    reverse(all(a));
    int t = 1;
    ll ans = 0, Max = a[1];
    while (1) {
        while (t + 1 < n && a[t + 1] == a[t]) ++t;
        if (t == n - 1) {
            int k = lg[t];
            ll D = a[0] - Max;
            ll A = D / k;
            Max += A * k;
            ans += 1ll * (k + 1) * A;
            ans += D % k;
            break;           
        } else {
            ll d = a[t] - a[t + 1];
            int k = lg[t]; //+=k
            if (1ll * k * d + Max <= a[0]) {
                Max += 1ll * k * d;
                ans += 1ll * (k + 1) * d;
            } else {
                ll D = a[0] - Max;
                ll A = D / k;
                Max += A * k;
                ans += 1ll * (k + 1) * A;
                ans += D % k;
                break;
            }
        }
        ++t;
    }
    cout << ans << '
';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    run();
    return 0;
}

K. Kleptography

签到。

Code

#include<cstdio>
using namespace std;
char enc[107];
char orn[107];
int main() {
	int n, m; scanf("%d%d", &n, &m);
	scanf("%s%s", orn+m-n, enc);
 
	for(int i=m-n-1, j=m-1; i>=0; i--, j--) {
		orn[i]=(enc[j]-orn[j]+26)%26+'a';
	}
	printf("%s
", orn);
}