题意:
现有(2^n,nleq 17)个参赛选手,开始(2cdot i,2cdot i-1)两两配对进行比赛。
比赛规则:每场比赛中赢的人会进入胜者组,输的人会进入败者组,一个人如果输两次那么直接出局。最终胜者组和败者组最终会只剩下一个人,决赛时只进行一场,赢的人就胜利。
现在你有(k)支心仪的队伍,你能够安排每场比赛的胜负,你希望看到尽量多的比赛中含有你的心仪队伍。
问这样的比赛数量最多为多少。
可以结合下图理解一下:
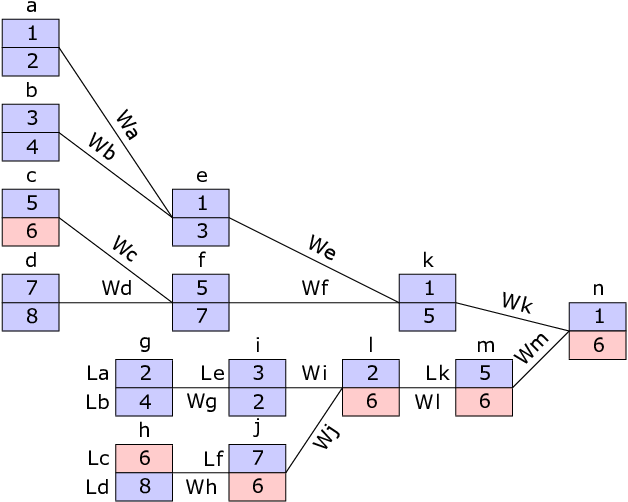
思路:
这个题初看不是很好思考,直接看了题解...接下来说说大概思路:
- 因为共有(2^n)个人,结合题意可以考虑合并两个(2^{i-1})到(2^i)。
- 如果想到了(dp),那么问题就转化为怎么定义(dp)状态和进行状态的合并。
- 最显然的想法就是(dp_{i,j,k})表示长度为(2^i),起点为(j),最终剩下的队伍是否为心仪的队伍。但是这种状态的定义不能考虑到输掉一场的人。因为两段合并时,不仅有赢的跟赢的打,还有输的跟输的打,最终再打一场才能决定最后的那个人。
- 因为上面的状态不能考虑到输的人,所以我们重新定义:(dp_{i,j,f_1,f_2})表示长度为(2^i),起点为(j),胜者组最后的队伍是否为心仪队伍,败者组最后的队伍是否为心仪队伍。
- 这样的话我们就可以考虑到所有的情况,只是需要在(dp)时手动枚举一下,最后一共有(8)种情况。
- 最终决赛的时候再单独判断一下即可。
这个题难就难在状态的定义,以及想清楚比赛中所遇到的一些情况。
细节见代码:
/*
* Author: heyuhhh
* Created Time: 2020/2/25 21:11:41
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '
'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '
'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = (1 << 17) + 5, M = 18;
int n, k;
int dp[M][N][2][2];
bool fan[N];
void run(){
cin >> n >> k;
for(int i = 1; i <= k; i++) {
int x; cin >> x;
fan[x] = 1;
}
memset(dp, -INF, sizeof(dp));
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= (1 << n); j += (1 << i)) {
if(i == 1) {
dp[i][j][fan[j]][fan[j + 1]] = (fan[j] | fan[j + 1]);
dp[i][j][fan[j + 1]][fan[j]] = (fan[j] | fan[j + 1]);
} else {
for(int x1 = 0; x1 < 2; x1++) {
for(int y1 = 0; y1 < 2; y1++) {
for(int x2 = 0; x2 < 2; x2++) {
for(int y2 = 0; y2 < 2; y2++) {
int cost = dp[i - 1][j][x1][y1] + dp[i - 1][j + (1 << (i - 1))][x2][y2];
if(x1 || x2) ++cost;
if(y1 || y2) ++cost;
dp[i][j][x1][x2] = max(dp[i][j][x1][x2], cost + (x2 | y1));
dp[i][j][x1][x2] = max(dp[i][j][x1][x2], cost + (x2 | y2));
dp[i][j][x1][y1] = max(dp[i][j][x1][y1], cost + (x2 | y1));
dp[i][j][x1][y2] = max(dp[i][j][x1][y2], cost + (x2 | y2));
dp[i][j][x2][x1] = max(dp[i][j][x2][x1], cost + (x1 | y1));
dp[i][j][x2][x1] = max(dp[i][j][x2][x1], cost + (x1 | y2));
dp[i][j][x2][y1] = max(dp[i][j][x2][y1], cost + (x1 | y1));
dp[i][j][x2][y2] = max(dp[i][j][x2][y2], cost + (x1 | y2));
}
}
}
}
}
}
}
int ans = 0;
for(int i = 0; i < 2; i++) {
for(int j = 0; j < 2; j++) {
ans = max(ans, dp[n][1][i][j] + (i | j));
}
}
cout << ans << '
';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
run();
return 0;
}