题意:
给出一个网格图类似于这样:
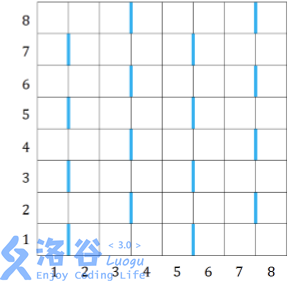
现在给出一个(n*m)大小的网格,之后会给出一些点,若某些点相连形成了如下的几个图案,那么就是不好的。
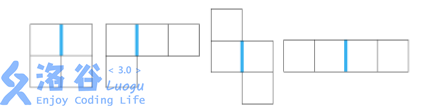
现在可以删去一些点,但删除每个点都有一些代价,问最终不出现上述图案的最小代价为多少。
思路:
初一看这图是什么乱七八糟的,但仔细观察能够发现它们的共性:对于蓝色的边两旁的格子,我们称为灰点;若有两个灰点相连,并且它们各自至少还连接了一个点,那么就是不合法的图案。
同时观察网格奇偶性,之后对网格奇偶染色。
然后初步思路为:源点连向所有白点,容量为白点权值;黑点向汇点连边,容量也为权值;然后中间为两两相连的灰点,权值为两者最小值。之后求个最小割就行了(相当于不存在一条白-灰-灰-黑的路径)。
但是这还有连边的细节需要分情况讨论一下,假设我们固定白点为起点,那么在不同行,灰点间的连边是不同的。
详见代码吧:
#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
//#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '
'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '
'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 5e5 + 5;
int c, r, n;
int x[N], y[N], w[N], col[N];
#define INF 0x3f3f3f3f
template <class T>
struct Dinic{
struct Edge{
int v, next;
T flow;
Edge(){}
Edge(int v, int next, T flow) : v(v), next(next), flow(flow) {}
}e[N << 1];
int head[N], tot;
int dep[N];
void init() {
memset(head, -1, sizeof(head)); tot = 0;
}
void adde(int u, int v, T w, T rw = 0) {
e[tot] = Edge(v, head[u], w);
head[u] = tot++;
e[tot] = Edge(u, head[v], rw);
head[v] = tot++;
}
bool BFS(int _S, int _T) {
memset(dep, 0, sizeof(dep));
queue <int> q; q.push(_S); dep[_S] = 1;
while(!q.empty()) {
int u = q.front(); q.pop();
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(!dep[v] && e[i].flow > 0) {
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[_T] != 0;
}
T dfs(int _S, int _T, T a) {
T flow = 0, f;
if(_S == _T || a == 0) return a;
for(int i = head[_S]; ~i; i = e[i].next) {
int v = e[i].v;
if(dep[v] != dep[_S] + 1) continue;
f = dfs(v, _T, min(a, e[i].flow));
if(f) {
e[i].flow -= f;
e[i ^ 1].flow += f;
flow += f;
a -= f;
if(a == 0) break;
}
}
if(!flow) dep[_S] = -1;
return flow;
}
T dinic(int _S, int _T) {
T max_flow = 0;
while(BFS(_S, _T)) max_flow += dfs(_S, _T, INF);
return max_flow;
}
};
Dinic <int> solver;
map <int , int> mp[N];
const int dx[] = {1, -1, 0, 0};
const int dy[] = {0, 0, 1, -1};
void run() {
for(int i = 1; i <= n; i++) {
cin >> x[i] >> y[i] >> w[i];
mp[x[i]][y[i]] = i;
if(y[i] % 2 == 0) {
if(x[i] % 4 == 0 || x[i] % 4 == 3) col[i] = 2;
else if((x[i] + y[i]) & 1) col[i] = 1;
else col[i] = 0;
} else {
if(x[i] % 4 == 1 || x[i] % 4 == 2) col[i] = 2;
else if((x[i] + y[i]) & 1) col[i] = 1;
else col[i] = 0;
}
}
solver.init();
dbg(mp[1][1]);
int s = 0, t = n + 1;
for(int i = 1; i <= n; i++) {
if(col[i] == 1) solver.adde(s, i, w[i]);
}
for(int i = 1; i <= n; i++) {
if(col[i] == 0) solver.adde(i, t, w[i]);
}
for(int i = 1; i <= n; i++) {
if(col[i] == 2) continue;
for(int j = 0; j < 4; j++) {
int curx = x[i] + dx[j], cury = y[i] + dy[j];
int id = mp[curx][cury];
if(id > 0 && col[id] == 2) {
if(col[i] == 0) {
solver.adde(id, i, INF);
}
else {
solver.adde(i, id, INF);
}
}
}
}
for(int i = 1; i <= n; i++) {
if(col[i] != 2) continue;
int curx, cury;
if(y[i] % 2) {
curx = x[i] + 1, cury = y[i];
} else {
curx = x[i] - 1, cury = y[i];
}
int id = mp[curx][cury];
if(id > 0 && col[id] == 2) {
solver.adde(i, id, min(w[id], w[i]));
}
}
int ans = solver.dinic(0, t);
cout << ans << '
';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
#ifdef Local
freopen("../input.in", "r", stdin);
freopen("../output.out", "w", stdout);
#endif
while(cin >> c >> r >> n) run();
return 0;
}