递归&算法基础
一、递归
递归函数的优点是定义简单,逻辑清晰。理论上,所有的递归函数都可以写成循环的方式,但循环的逻辑不如递归清晰。
使用递归函数需要注意防止栈溢出。在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出。
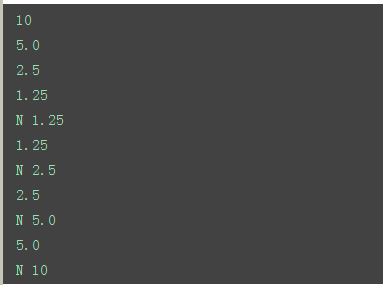
1 2 3 4 5 6 7 8 | def calc(n): print(n) if n/2>1: ret = calc(n/2) print(ret) print('N',n) return ncalc(10) |
二、二分法
主要使用折半查找算法和利用递归函数来实现。因为每次取中间数字后,都会产生左右两个数组,
需要使用队列把数组存起来,然后输入递归函数内计算中间数字。递归函数终止条件是:1)中间数字
与左边最小的数字相邻;2)中间数字与右边最大的数字相邻。
代码实现:
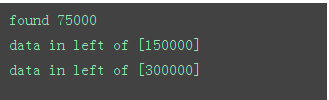
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | def binary_search(data_source,find_num): mid = int(len(data_source)/2) if len(data_source) >1: if data_source[mid] > find_num: binary_search(data_source[:mid],find_num) print('data in left of [%s]'%data_source[mid]) elif data_source[mid] < find_num: binary_search(data_source[mid:],find_num) print('data in right of [%s]'%data_source[mid]) else: print('found',data_source[mid]) else: print('cannot found')if __name__ == '__main__': data = list(range(1,600000)) binary_search(data,75000) |
三、用递归实现斐波那契数列
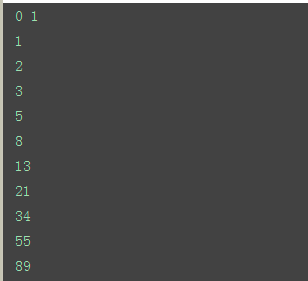
1 2 3 4 5 6 7 8 | def fun(arg0,arg1,stop): if arg0 == 0: print(arg0,arg1) arg2 = arg0 + arg1 if arg2 < stop : print(arg2) fun(arg1,arg2,stop)fun(0,1,1000) |
四、二维数组转换
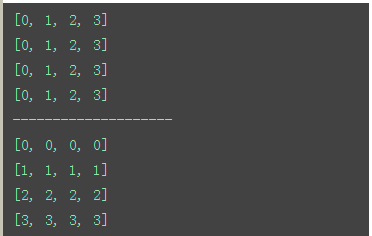
需求:生成一个4*4的二维数组并将其顺时针旋转90度
核心思想:数组下标的对应关系可以一一对应转换。
1 2 3 4 5 6 7 8 9 10 11 | data = [[col for col in range(4)] for row in range(4)]for i in data: print(i)for r_index,row in enumerate(data): for c_index in range(r_index,len(row)): tmp = data[c_index][r_index] data[c_index][r_index] = row[c_index] data[r_index][c_index] = tmpprint('--------------------')for i in data: print(i) |
五、冒泡排序
1 2 3 4 5 6 7 8 9 10 | #!/usr/bin/env pythondata = [10,4,33,21,54,3,8,11,5,22,2,1,17,13,6]for i in range(len(data)): for j in range(len(data)-1-i): if data[j] > data[j+1]: tmp = data[j+1] data[j+1] = data[j] data[j] = tmp #data[j],data[j+1] = data[j+1],data[j] #这种方式也可以 print(data) |

六、时间复杂度
1 2 3 4 5 | for (i=1; i<=n; i++) x++;for (i=1; i<=n; i++) for (j=1; j<=n; j++) x++; |
第一个for循环的时间复杂度为Ο(n),第二个for循环的时间复杂度为Ο(n2),则整个算法的时间复杂度为Ο(n+n2)=Ο(n2)。
常数时间
若对于一个算法,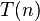 的上界与输入大小无关,则称其具有常数时间,记作
的上界与输入大小无关,则称其具有常数时间,记作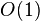 时间。一个例子是访问数组中的单个元素,因为访问它只需要一条指令。但是,找到无序数组中的最小元素则不是,因为这需要遍历所有元素来找出最小值。这是一项线性时间的操作,或称
时间。一个例子是访问数组中的单个元素,因为访问它只需要一条指令。但是,找到无序数组中的最小元素则不是,因为这需要遍历所有元素来找出最小值。这是一项线性时间的操作,或称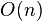 时间。但如果预先知道元素的数量并假设数量保持不变,则该操作也可被称为具有常数时间。
时间。但如果预先知道元素的数量并假设数量保持不变,则该操作也可被称为具有常数时间。
对数时间
若算法的T(n) = O(log n),则称其具有对数时间
对数时间的算法是非常有效的,因为每增加一个输入,其所需要的额外计算时间会变小。
递归地将字符串砍半并且输出是这个类别函数的一个简单例子。它需要O(log n)的时间因为每次输出之前我们都将字符串砍半。 这意味着,如果我们想增加输出的次数,我们需要将字符串长度加倍。
线性时间
如果一个算法的时间复杂度为O(n),则称这个算法具有线性时间,或O(n)时间。非正式地说,这意味着对于足够大的输入,运行时间增加的大小与输入成线性关系。例如,一个计算列表所有元素的和的程序,需要的时间与列表的长度成正比。
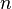 而呈
而呈