Problem Description
When the winter holiday comes, a lot of people will have a trip. Generally, there are a lot of souvenirs to sell, and sometimes the travelers will buy some ones with pleasure. Not only can they give the souvenirs to their friends and families as gifts, but
also can the souvenirs leave them good recollections. All in all, the prices of souvenirs are not very dear, and the souvenirs are also very lovable and interesting. But the money the people have is under the control. They can’t buy a lot, but only a few.
So after they admire all the souvenirs, they decide to buy some ones, and they have many combinations to select, but there are no two ones with the same kind in any combination. Now there is a blank written by the names and prices of the souvenirs, as a top
coder all around the world, you should calculate how many selections you have, and any selection owns the most kinds of different souvenirs. For instance:
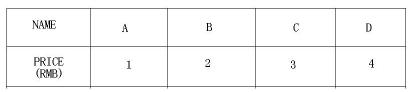
And you have only 7 RMB, this time you can select any combination with 3 kinds of souvenirs at most, so the selections of 3 kinds of souvenirs are ABC (6), ABD (7). But if you have 8 RMB, the selections with the most kinds of souvenirs are ABC (6), ABD (7), ACD (8), and if you have 10 RMB, there is only one selection with the most kinds of souvenirs to you: ABCD (10).

And you have only 7 RMB, this time you can select any combination with 3 kinds of souvenirs at most, so the selections of 3 kinds of souvenirs are ABC (6), ABD (7). But if you have 8 RMB, the selections with the most kinds of souvenirs are ABC (6), ABD (7), ACD (8), and if you have 10 RMB, there is only one selection with the most kinds of souvenirs to you: ABCD (10).
Input
For the first line, there is a T means the number cases, then T cases follow.
In each case, in the first line there are two integer n and m, n is the number of the souvenirs and m is the money you have. The second line contains n integers; each integer describes a kind of souvenir.
All the numbers and results are in the range of 32-signed integer, and 0<=m<=500, 0<n<=30, t<=500, and the prices are all positive integers. There is a blank line between two cases.
In each case, in the first line there are two integer n and m, n is the number of the souvenirs and m is the money you have. The second line contains n integers; each integer describes a kind of souvenir.
All the numbers and results are in the range of 32-signed integer, and 0<=m<=500, 0<n<=30, t<=500, and the prices are all positive integers. There is a blank line between two cases.
Output
If you can buy some souvenirs, you should print the result with the same formation as “You have S selection(s) to buy with K kind(s) of souvenirs”, where the K means the most kinds of souvenirs you can buy, and S means the numbers of the combinations you can
buy with the K kinds of souvenirs combination. But sometimes you can buy nothing, so you must print the result “Sorry, you can't buy anything.”
Sample Input
2
4 7
1 2 3 4
4 0
1 2 3 4
Sample Output
You have 2 selection(s) to buy with 3 kind(s) of souvenirs.
Sorry, you can't buy anything.
这题可以用01背包,给你n个背包以及它们的重量,再给你背包的总重量m,让你求取得最大的物品个数是多少,共有几种方案。之前状态转移方程写错了错了好多次,后来改对了。
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<vector>
#include<map>
#include<queue>
#include<stack>
#include<string>
#include<algorithm>
using namespace std;
#define inf 88888888
int w[50],dp[600][2];
int main()
{
int n,m,i,j,T,num,num1,fas,minx,flag;
scanf("%d",&T);
while(T--)
{
minx=inf;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++){
scanf("%d",&w[i]);
if(w[i]<minx)minx=w[i];
}
if(m<minx){
printf("Sorry, you can't buy anything.
");continue;
}
for(i=1;i<=n;i++){
for(j=0;j<=m;j++){
dp[j][0]=0;dp[j][1]=1;
}
}
for(i=1;i<=n;i++){
for(j=m;j>=w[i];j--){
if(dp[j-w[i]][0]+1>dp[j][0]){
dp[j][0]=dp[j-w[i]][0]+1;dp[j][1]=dp[j-w[i]][1];
}
else if(dp[j-w[i]][0]+1==dp[j][0]){
dp[j][1]+=dp[j-w[i]][1];
}
}
}
printf("You have %d selection(s) to buy with %d kind(s) of souvenirs.
",dp[m][1],dp[m][0]);
}
return 0;
}