Famil Door’s City map looks like a tree (undirected connected acyclic graph) so other people call it Treeland. There are n intersections in the city connected by n - 1 bidirectional roads.
There are m friends of Famil Door living in the city. The i-th friend lives at the intersection ui and works at the intersection vi. Everyone in the city is unhappy because there is exactly one simple path between their home and work.
Famil Door plans to construct exactly one new road and he will randomly choose one among n·(n - 1) / 2 possibilities. Note, that he may even build a new road between two cities that are already connected by one.
He knows, that each of his friends will become happy, if after Famil Door constructs a new road there is a path from this friend home to work and back that doesn't visit the same road twice. Formally, there is a simple cycle containing both ui and vi.
Moreover, if the friend becomes happy, his pleasure is equal to the length of such path (it's easy to see that it's unique). For each of his friends Famil Door wants to know his expected pleasure, that is the expected length of the cycle containing both ui and vi if we consider only cases when such a cycle exists.
The first line of the input contains integers n and m (2 ≤ n, m ≤ 100 000) — the number of the intersections in the Treeland and the number of Famil Door's friends.
Then follow n - 1 lines describing bidirectional roads. Each of them contains two integers ai and bi (1 ≤ ai, bi ≤ n) — the indices of intersections connected by the i-th road.
Last m lines of the input describe Famil Door's friends. The i-th of these lines contain two integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — indices of intersections where the i-th friend lives and works.
For each friend you should print the expected value of pleasure if he will be happy. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely: let's assume that your answer is a, and the answer of the jury is b.
The checker program will consider your answer correct, if 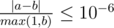 .
.
4 3 2 4 4 1 3 2 3 1 2 3 4 1
4.00000000 3.00000000 3.00000000
3 3 1 2 1 3 1 2 1 3 2 3
2.50000000 2.50000000 3.00000000
题意:给你一棵节点数为n的树,随机地在树上的任意两个点连一条边,给你m个询问,每次询问两个点,问连一条边后如果这两个点能在简单环中,简单环的期望是多少。
简单环即这两个点在一个环上,这个环是没有重边的。
思路:这里先设置几个变量dep[i]:i节点的深度,这里记dep[0]=0,dep[1]=1;sz[i]:i节点的子树的节点总数;f[i][j]:i节点的2^j倍父亲;sdown[i]:i节点子树中的所有点到i节点的距离和;sall[i]:所有点到i节点的距离和;t=lca(u,v).
先考虑lca(u,v)!=u && lca(u,v)!=v的情况,想要使得u,v都在简单环中,那么连边的两个端点一定是一个在u的子树中,另一个在v的子树中,且连边的方案数为sz[u]*sz[v],那么我们得到的期望值是sdown[u]/sz[u]+sdown[v]/sz[v]+1+dep[u]+dep[v]-2*dep[t].这里dep[u]+dep[v]-2*dep[t]+1是每一个形成的简单环都有的长度,所以可以先加上去.
然后考虑lca(u,v)==u || lca(u,v)==v的情况,不妨假设lca(u,v)=v,那么连边的两个端点一端一定在u的子树中,另一端在v的上面,即树上的所有点除去不包括u这个节点的子树,我们得到的期望值是sdown[u]/sz[u]+(sall[v]-sdown[v1]-sz[v1])/(n-sz[v1]) (v1是u,v路径上v的子节点).
第一次dfs先求出sdown[i],然后第二次dfs就能求出sall[i]了.
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<string>
#include<algorithm>
using namespace std;
typedef long long ll;
typedef long double ldb;
#define inf 99999999
#define pi acos(-1.0)
#define maxn 100050
int sz[maxn],dep[maxn],f[maxn][23];
ll sdown[maxn],sall[maxn];
int n;
struct edge{
int to,next;
}e[2*maxn];
int first[maxn];
void dfs1(int u,int father,int deep)
{
int i,j,v;
dep[u]=dep[father]+1;
sz[u]=1;sdown[u]=0;
for(i=first[u];i!=-1;i=e[i].next){
v=e[i].to;
if(v==father)continue;
f[v][0]=u;
dfs1(v,u,dep[u]);
sz[u]+=sz[v];
sdown[u]+=sdown[v]+sz[v];
}
}
void dfs2(int u,int father)
{
int i,j,v;
for(i=first[u];i!=-1;i=e[i].next){
v=e[i].to;
if(v==father)continue;
sall[v]=sall[u]+n-2*sz[v]; //这里是主要的公式,可以这样理解:所有点到父亲节点u的距离和sall[u]已经算出来了,那么算v这个节点的时候,不在v子树范围内的点到v的距离都多了1,所以加上n-sz[v],v的子树的点到v的距离都减少了1,所以要减去sz[v].
dfs2(v,u);
}
}
void init()
{
dep[0]=0;
dfs1(1,0,0);
sall[1]=sdown[1];
dfs2(1,0);
}
int lca(int x,int y){
int i;
if(dep[x]<dep[y]){
swap(x,y);
}
for(i=20;i>=0;i--){
if(dep[f[x][i] ]>=dep[y]){
x=f[x][i];
}
}
if(x==y)return x;
for(i=20;i>=0;i--){
if(f[x][i]!=f[y][i]){
x=f[x][i];y=f[y][i];
}
}
return f[x][0];
}
int up(int u,int deep)
{
int i,j;
for(i=20;i>=0;i--){
if((1<<i)<=deep){
u=f[u][i];
deep-=(1<<i);
}
}
return u;
}
int main()
{
int m,i,j,tot,c,d,v,u,k;
double sum;
while(scanf("%d%d",&n,&m)!=EOF)
{
tot=0;
memset(first,-1,sizeof(first));
for(i=1;i<=n-1;i++){
scanf("%d%d",&c,&d);
tot++;
e[tot].next=first[c];e[tot].to=d;
first[c]=tot;
tot++;
e[tot].next=first[d];e[tot].to=c;
first[d]=tot;
}
init();
for(k=1;k<=20;k++){
for(i=1;i<=n;i++){
f[i][k]=f[f[i][k-1]][k-1];
}
}
for(i=1;i<=m;i++){
scanf("%d%d",&u,&v);
int t=lca(u,v);
sum=(double)(dep[u]+dep[v]-2*dep[t])+1;
if(t==u || t==v){
if(t==u)swap(u,v);
int v1=up(u,dep[u]-dep[v]-1);
ll num1=sall[v]-sdown[v1]-sz[v1];
sum+=(double)sdown[u]/(double)sz[u]+(double)(num1)/(double)(n-sz[v1]);
printf("%.10f
",sum);
}
else{
sum+=(double)sdown[u]/(double)sz[u]+(double)sdown[v]/(double)sz[v];
printf("%.10f
",sum);
}
}
}
return 0;
}