566. 重塑矩阵
在MATLAB中,有一个非常有用的函数reshape,它可以将一个m x n矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。
给你一个由二维数组mat表示的m x n矩阵,以及两个正整数r和c,分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。
如果具有给定参数的reshape操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
示例 1:
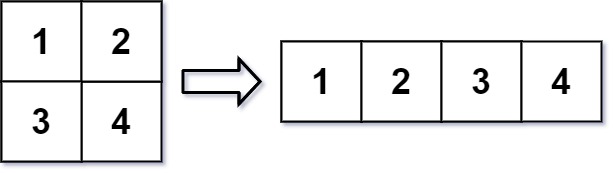
输入:mat = [[1,2],[3,4]], r = 1, c = 4
输出:[[1,2,3,4]]
示例 2:
输入:mat = [[1,2],[3,4]], r = 2, c = 4
输出:[[1,2],[3,4]]

class Solution:
def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:
tem = []
tem1 = []
for i in range(len(mat)):
for j in range(len(mat[i])):
tem.append(mat[i][j])
if r * c == len(tem):
for i in range(r):
tem2 = []
for j in range(c):
tem2.append(tem[0])
tem.pop(0)
tem1.append(tem2)
return tem1
else:
return mat
执行用时:136 ms, 在所有 Python3 提交中击败了5.24%的用户
内存消耗:15.5 MB, 在所有 Python3 提交中击败了76.98%的用户
这不是慢这是在打磨!在日本我可以当个仙人的!
- 根据题目要求,我们可以一开始先判断转换后矩阵的维度是否匹配转换前矩阵的维度,如果不匹配则直接返回输入矩阵即可
- 新建一个矩阵作为返回值
- 遍历 r x c 个元素的同时找到两个矩阵间对应的位置。这是一个简单的除法问题:已知第i个元素,求在矩阵r行c列中的位置,即为i / c 行和 i % c 列。
class Solution:
def matrixReshape(self, nums, r, c):
row, col = len(nums), len(nums[0])
if row * col != r * c:
return nums
res = [[None] * c for _ in range(r)]
for i in range(r*c):
res[i//c][i%c] = nums[i//col][i%col]
return res
执行用时:28 ms, 在所有 Python3 提交中击败了96.82%的用户
内存消耗:15.7 MB, 在所有 Python3 提交中击败了14.25%的用户
118. 杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。在「杨辉三角」中,每个数是它左上方和右上方的数的和。
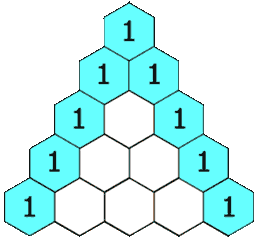
**输入: **numRows = 5
**输出: **[[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
l = [[1]]
for i in range(1, numRows):
l.append([1])
for j in range(1, i):
l[i].append(l[i-1][j-1]+l[i-1][j])
l[i].append(1)
return l
执行用时:36 ms, 在所有 Python3 提交中击败了40.58%的用户
内存消耗:15.1 MB, 在所有 Python3 提交中击败了13.05%的用户
凑合用~