模拟70
 (它是个正方形~)
(它是个正方形~)
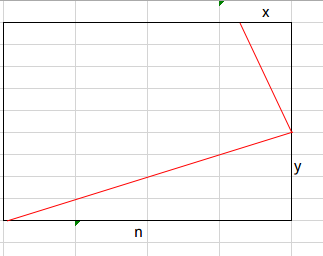
由相似得 $frac{n}{n-y}=frac{y}{x}$ 得$ nx=(n-y)y $于是$x=frac{(n-y)y}{n} $,有$n|ny$,故 $n|y^2 $
可以直接筛出n的质因子及其个数,则y包含 n的每一种质因子的个数至少为n包含个数的一半,至于y的其它因子则随便,只要y不超过n就行
所以答案就是 n除以我们算出来的那个最小的y,然后因为y不能取到n,要-1,又因为有四个顶点,每一个顶点对应边又有两种组合,最后乘上8

#include<iostream> #include<cstdio> #include<cmath> using namespace std; long long n,ans; long long prm[110],num[110]; int main(){ // freopen("1.in","r",stdin); // freopen("c.out","w",stdout); while(scanf("%lld",&n)&&n!=0){ long long x=n; prm[0]=0; for(register int i=2;i<=sqrt(x);i++){ if(x%i==0){ prm[++prm[0]]=i; num[prm[0]]=0; while(x%i==0) num[prm[0]]++,x/=i; } } if(x!=1) prm[++prm[0]]=x,num[prm[0]]=1; for(register int i=1;i<=prm[0];i++){ for(register int j=1;j<=(num[i]+1)/2;j++){ n/=prm[i]; } } printf("%lld ",(n-1)*8); } }
n^2DP +减枝

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m,a[41000],tmp[41000],num,f[41000];
int main(){
//freopen("2.in","r",stdin);
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++) scanf("%d",&a[i]);
int cet=0;
for(register int i=1;i<=n;i++){
if(a[i]!=a[i-1]) a[++cet]=a[i];
}
n=cet;
memset(f,0x3f,sizeof(f));
memset(tmp,-1,sizeof(tmp));
for(register int i=0;i<n;i++){
f[i]=min(f[i],i);
int x=0;
for(register int j=i+1;j<=n;j++){
if(tmp[a[j]]!=i) tmp[a[j]]=i,x++;
if(f[i]+x*x>n) break;
if(f[j]>f[i]+x*x) f[j]=f[i]+x*x;
}
}
printf("%d
",f[n]);
}
骆驼 (EJOI2017)(未填)
暴力找5 *5 的格子的方案,发现从任意一个点开始到任一一点结束都可以找到合法方案,那么将一堆5*5的块拼起来就组成了解,至于怎么拼则随意
模拟71
首先,先确定题意,题意并不是问非空子集一共有多少划分方式使得分数相同,而是 有多少非空子集可以划分成分数相同的两部分
考虑从一个人的视角出发,dfs枚举状态。统计两人的分差,选择一个题,分数加 $M_i$,对方选择该题,分数减$M_i$ ,那么可以统计出任意分差的各种状态
$meet in the middle $ 先统计前$ n/2$ 的各种分差(比如 $x$)的各种状态,用哈希表记录,然后 dfs 后n/2 的状态及分差(比如$ y$),只需要查找前面的一个分差 $x$使得 $x+y=0$(分差为0),并记录状态的并(为了不重不漏),统计 答案
hashmap 可能会有冲撞,所以在前n/2个题记录状态的同时,要记录原来的分差(不是取模之后的),在查询是进行比对,防止出现两个分差不一样,而取模后一样导致的查到另一种分差

#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int n,a[25],v[1<<21],ans,base1,base2; const int mod=23333; struct Hash{ int head[23334],tot,to[300000],nex[300000],c[300000]; void insert(int x,int sta){ int las=x; x=(x%mod+mod)%mod; for(register int i=head[x];i;i=nex[i]){ if(c[i]==las&&to[i]==sta) return; } to[++tot]=sta,nex[tot]=head[x],head[x]=tot,c[tot]=las; } void find(int x,int sta){ int las=x; x=(x%mod+mod)%mod; for(register int i=head[x];i;i=nex[i]){ if(las==c[i]&&!v[to[i]|sta]) ans++,v[to[i]|sta]=1; } } }Ha; void dfs(int d,int sum,int sta){ if(d==base1+1){ if(sta==0) return; if(sum==0){ if(!v[sta]) ans++,v[sta]=1; } Ha.insert(sum,sta); return; } dfs(d+1,sum,sta); dfs(d+1,sum+a[d],sta|(1<<(d-1))); dfs(d+1,sum-a[d],sta|(1<<(d-1))); } void DFS(int d,int sum,int sta){ if(d==base2+1){ if(sta==0) return; if(sum==0){ if(!v[sta]) ans++,v[sta]=1; } Ha.find(0-sum,sta); return; } DFS(d+1,sum,sta); DFS(d+1,sum+a[d+base1],sta|(1<<(base1+d-1))); DFS(d+1,sum-a[d+base1],sta|(1<<(base1+d-1))); } int main(){ scanf("%d",&n); base1=n/2,base2=n-base1; for(register int i=1;i<=n;i++) scanf("%d",&a[i]); dfs(1,0,0); DFS(1,0,0); printf("%d ",ans); }
简单DP?(不会)
枚举 x,二分最重背包重量,统计答案,一些优化减枝——如果$(a_i+x)%p $ 大于 当前ans,不在二分直接跳过

#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> using namespace std; int n,p,k; int a[11000],c[11000],ans=0x7fffffff; char judge(int x,int upw){ int num=1,las=0; for(register int i=1;i<=n;i++){ c[i]=(a[i]+x)%p; if(c[i]>upw) return 0; } for(register int i=1;i<=n;i++){ las+=c[i]; if(las>upw) las=c[i],num++; if(num>k) return 0; } return num<=k; } int main(){ srand(time(0)); scanf("%d%d%d",&n,&p,&k); for(register int i=1;i<=n;i++) scanf("%d",&a[i]); for(register int i=0;i<p;i++){ if(!judge(i,ans)) continue; int l=0,r=ans,mid,cet=-1; while(l<=r){ mid=(l+r)>>1; if(judge(i,mid)) r=mid-1,cet=mid; else l=mid+1; } if(cet>=0&&cet<ans) ans=cet; } printf("%d ",ans); }
模拟72
不开龙龙见祖宗!
先处理出$p$需要$lnum$个左括号与$S$匹配,$q$需要$rnum$右括号与$S$匹配,然后可以算出有多少对自由括号 $num=frac{n-m-lnum-rnum}{2}$
枚举 $p$中的自由括号对$i$,零散的左括号$j+lnum$,那么$q$中的自由括号对就是 $num-i-j$,零散右括号$j+rnum$
把左括号看成+1,右括号-1,显然是卡特兰数(kuku~,我推了俩小时在发现,我辣鸡~)
$ans=sumlimits_{i=0}^{num}sumlimits_{j=0}^{num-i}(C_{i+i+j+lnum}^{i+j+lnum}-C_{i+i+j+lnum}^{i+j+lnum+1})*(C_{num-i-j+num-i+rnum}^{num-i+rnum}-C_{num-i-j+num-i+rnum}^{num-i+rnum+1}) $

#include<iostream> #include<cstdio> using namespace std; int n,m,lnum,rnum,num,C[2100][2100]; char a[110000]; long long ans; const int mod=1e9+7; long long cal(int i,int j,int num,int lnum,int rnum){ int w1=i,w2=i+j+lnum,w3=num-i-j,w4=num-i+rnum; long long cnt=1ll*(C[w1+w2][w2]-C[w1+w2][w2+1]+mod)%mod*((C[w3+w4][w4]-C[w3+w4][w4+1]+mod)%mod)%mod; return cnt%mod; } int main(){ //freopen("1.in","r",stdin); scanf("%d%d%s",&n,&m,a+1); if(n&1){ puts("0"); return 0; } for(register int i=1;i<=m;i++){ if(a[i]=='(') rnum++; else if(a[i]==')'){ if(rnum) rnum--; else lnum++; } } if(n<m+rnum+lnum){ puts("0"); return 0; } num=(n-m-rnum-lnum)/2; for(register int i=0;i<=n-m;i++){ C[i][0]=1; for(register int j=1;j<=i;j++) C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod; } for(register int i=0;i<=num;i++) for(register int j=0;j<=num-i;j++) ans=(ans+cal(i,j,num,lnum,rnum))%mod; printf("%lld ",ans%mod); }
简单的期望 (好题)
DP
$f[i][j][k][0/1],j<=(1<<8)-1 $,表示第i次操作后,x的前7位(0~7位),第8位为$0/1$,且从第8位开始有k个和第8位一样 的概率
至于为什么只存前7位的状态,是因为,当第8位为1,前7位为1,后面还有k个1,此时加1,会导致从0为到8+k为全变成0,但是再想进位还需要至少$2^8$次加+1才可以,所以最多进位出8位最多一次
转移很好想,我打了6个转移方程,两个乘2,两个加1(加1以 j是否为(1<<8)-1分为两种),共6个

#include<iostream> #include<cstdio> using namespace std; int n,x; double p,f[210][1<<9][232][2]; int main(){ scanf("%d%d%lf",&x,&n,&p); p/=100.0; int base=(1<<8)-1; int las=x,num=1; for(int i=9,y=x>>9;i<=230&&y;i++,y>>=1){ if((y&1)!=((x>>8)&1)) break; num++; } f[0][x&base][num][(x>>8)&1]=1; for(register int i=1;i<=n;i++){ for(register int j=0;j<=base;j++){ for(register int k=1;k<=230;k++){ f[i][(j<<1)&base][k+1][(j>>7)&1]+=f[i-1][j][k][(j>>7)&1]*p; f[i][(j<<1)&base][1][(j>>7)&1]+=f[i-1][j][k][(j>>7)&1^1]*p; if(j<base){ f[i][(j+1)&base][k][1]+=f[i-1][j][k][1]*(1.0-p); f[i][(j+1)&base][k][0]+=f[i-1][j][k][0]*(1.0-p); } else{ f[i][0][1][1]+=f[i-1][j][k][0]*(1.0-p); f[i][0][k][0]+=f[i-1][j][k][1]*(1.0-p); } } } } double ans=0; for(register int i=0;i<=base;i++){ for(register int k=1;k<=230;k++){ int num=0,x=i; for(int l=0;l<=7&&!(x&1);l++,x>>=1) num++; ans+=num*f[n][i][k][1]; if(num==8) ans+=(num+k)*f[n][i][k][0]; else ans+=num*f[n][i][k][0]; } } printf("%.10lf ",ans); }
考试时想到了判奇环,然后就不会了
正解其实挺简单,先dfs黑白染色判奇环,并记录所在联通块,如果有奇环直接$pus("-1")+return 0$,否则找每一个联通块里两点最短路的最大值加和
因为一个点到另一个点如果有两条路径,那么长的和短的合并会变成短的那一个,而我们要找最长链所以找最短路的最大值
至于加和则是由于两个联通块可以将一个的根与另一个的叶子合并使两个链连起来,所以加和

#include<iostream> #include<cstdio> #include<queue> #include<cstring> using namespace std; int n,m,tot,to[210000],nex[210000],head[110000],belong[1100],dfn[1100],dis[1100][1100],v[1100][1100],ans[1100000],cet; queue<int>q; void add(int x,int y){ to[++tot]=y,nex[tot]=head[x],head[x]=tot; } int dfs(int x){ belong[x]=cet; for(register int i=head[x];i;i=nex[i]){ int y=to[i]; if(dfn[y]==dfn[x]) return -1; if(dfn[y]) continue; dfn[y]=3-dfn[x]; if(dfs(y)==-1) return -1; } return 0; } void BFS(int bg){ v[bg][bg]=1; dis[bg][bg]=0; q.push(bg); while(q.size()){ int x=q.front();q.pop(); for(register int i=head[x];i;i=nex[i]){ int y=to[i]; if(dis[bg][y]>dis[bg][x]+1){ dis[bg][y]=dis[bg][x]+1; ans[belong[bg]]=max(ans[belong[bg]],dis[bg][y]); if(!v[bg][y]) q.push(y),v[bg][y]=1; } } } } int main(){ scanf("%d%d",&n,&m); for(register int i=1,x,y;i<=m;i++) scanf("%d%d",&x,&y),add(x,y),add(y,x); for(register int i=1;i<=n;i++){ if(!belong[i]){ ++cet;dfn[i]=1; if(dfs(i)==-1){ puts("-1"); return 0; } } } memset(dis,0x3f,sizeof(dis)); for(register int i=1;i<=n;i++){ BFS(i); } long long Ans=0; for(register int i=1;i<=cet;i++){ Ans+=ans[i]; } printf("%lld ",Ans); }
总结: 这几次总是考的特别渣,思路上没有别人快,好不容易想到一点,还经常犯低错,蓝瘦。
