java使用栈
public static void main(String[] args) { Stack<Integer> stack = new Stack(); stack.push(1); System.out.println(stack.peek()); System.out.println(stack.isEmpty()); System.out.println(stack.pop()); System.out.println(stack.isEmpty()); stack.push(1); stack.push(2); stack.push(3); stack.push(4); stack.push(5); System.out.println(stack.search(5)); System.out.println(stack.indexOf(1)); System.out.println(stack.indexOf(31)); System.out.println(stack.contains(1)); }
递归实现汉诺塔
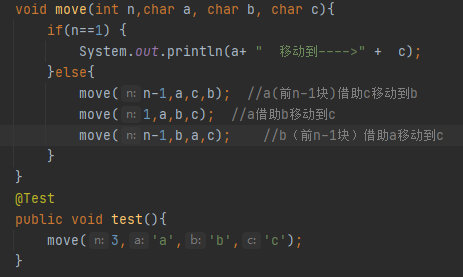
其实递归也就是不断的把子函数不断入栈的过程,直到n==1的时候再出栈不断返回计算结果的过程。
java使用队列
//Quene类型 @Test public void test2() throws InterruptedException { LinkedBlockingQueue linkedBlockingQueuee = new LinkedBlockingQueue(); linkedBlockingQueuee.add(1); linkedBlockingQueuee.add(2); linkedBlockingQueuee.add("2"); linkedBlockingQueuee.offer(22); System.out.println(linkedBlockingQueuee.peek()); //1 System.out.println(linkedBlockingQueuee.element()); //1 System.out.println(linkedBlockingQueuee.poll()); //1 System.out.println(linkedBlockingQueuee.remove()); //2 System.out.println(linkedBlockingQueuee.take()); //2 } //双向队列LinkedList @Test public void test3(){ LinkedList list = new LinkedList<>(); list.add("1"); list.addFirst("2"); list.addLast("3");; System.out.println(list); //[2, 1, 3] LinkedList list1 = new LinkedList<>(); list1.addAll(list); System.out.println(list1.element()); //2 System.out.println(list1.removeFirst()); //2 list1.add(list); // System.out.println(list1.addAll(list)); System.out.println(list1); //[1, 3, [2, 1, 3]] list1.remove(0); //[3, [2, 1, 3]] System.out.println(list1); System.out.println(list1.contains("3")); Collections.sort(list); System.out.println(list); //[1, 2, 3] }
kmp算法
https://www.cnblogs.com/henuliulei/p/10800027.html
package base; import java.util.Arrays; import java.util.Scanner; public class KMP { int[] get_next(String str,int[] next,int length){ int i =1; next[1]=0; int j=0; while (i<length){ if(j==0 || str.charAt(i)==str.charAt(j)){ ++i; ++j; next[i] = j; }else{ j=next[j]; } } return next; } int kmp(int [] next,String TT,int lengthT,String M,int lengthM){ int j=1; int i=0; while (i<lengthT && j<=lengthM){ if(j==0 || TT.charAt(i)==M.charAt(j-1)){ i++; j++; }else{ j=next[j]; } } if(j>lengthM){ return i-lengthM; }else{ return -1; } } public static void main(String[] args) { String T = ""; String M = ""; Scanner scanner = new Scanner(System.in); T = scanner.next(); M = scanner.next(); int next[] = new int[M.length()+1]; Arrays.fill(next,0); int lengthT = T.length(); int lengthM = M.length(); KMP kmps = new KMP(); int[] next1 = kmps.get_next(M, next, lengthM); System.out.println(Arrays.toString(next1)); int m = kmps.kmp(next1,T,lengthT,M,lengthM); System.out.println(m); } }
稀疏矩阵快速转置
相比于之前的遍历整个矩阵,找到非零元素在新矩阵进行放置的方法,该方法就是把非零元素进行一轮遍历,找到每列元素的个数,进而提前确定每列元素插入时应该放第几个位置,这样遍历一遍三元组就可以正确的放置元素到正确的位置,
而不需要遍历原始矩阵。使复杂度降低。矩阵快速转置算法详解 (biancheng.net)
package base; import java.lang.reflect.Array; import java.util.ArrayList; import java.util.Arrays; public class matrixTranspose { public static void main(String[] args) { int [] ArrayT= {1,2,12,1,3,9,3,1,-3,3,6,14,4,3,24,5,2,18,6,1,15,6,4,-7}; int ArrayM[] = new int[24]; Arrays.fill(ArrayM,0); int ArrayNum[] = new int [6]; Arrays.fill(ArrayNum,0); int pos[] =new int [6]; Arrays.fill(pos,0); for (int i = 0; i < ArrayT.length; i++) { if (i % 3 == 1) { ArrayNum[ArrayT[i] - 1]++; } } System.out.println(Arrays.toString(ArrayNum)); for (int i = 1; i <ArrayNum.length; i++) { pos[i] = pos[i-1] + ArrayNum[i-1]*3; } System.out.println(Arrays.toString(pos)); for (int i = 0; i < ArrayT.length; i++) { if(i%3==1){ ArrayM[pos[ArrayT[i]-1]] = ArrayT[i]; ArrayM[pos[ArrayT[i]-1]+1] = ArrayT[i-1]; ArrayM[pos[ArrayT[i]-1]+2] = ArrayT[i+1]; pos[ArrayT[i]-1] +=3; } } System.out.println(Arrays.toString(ArrayM)); } }
二叉树的性质:
二叉树的第i层至多有2^(i-1)个结点,一个二叉树最多有2^i-1个结点,终端结点个数等于度数为2的结点个数+1:n1=n2+1
具有n个结点的完全二叉树的深度为log2n(向下取正)+1。左孩子为2*i,右孩子为2*i+1。完全二叉树是满二叉树的子集,最下一层右边孩子不大于满二叉树最下层。
先序遍历,中序遍历,后序遍历java代码演示,建立一个类构件树,然后使用递归算法遍历树、
package base; public class 先序中序后序遍历 { public static Node init(){ Node J = new Node(8, null, null); Node H = new Node(4, null, null); Node G = new Node(2, null, null); Node F = new Node(7, null, J); Node E = new Node(5, H, null); Node D = new Node(1, null, G); Node C = new Node(9, F, null); Node B = new Node(3, D, E); Node A = new Node(6, B, C); return A; } public static void printNode(Node node){ if(node != null){ System.out.print(node.getData()); System.out.print(" "); } } public static void before(Node node){ printNode(node); if(node.getLeftNode() != null){ before(node.getLeftNode()); } if(node.getRightNode() != null){ before(node.getRightNode()); } } public static void middle(Node node){ if(node.getLeftNode() != null){ middle(node.getLeftNode()); } printNode(node); if(node.getRightNode() != null){ middle(node.getRightNode()); } } public static void after(Node node){ if(node.getLeftNode() != null){ after(node.getLeftNode()); } if(node.getRightNode() != null){ after(node.getRightNode()); } printNode(node); } public static void main(String[] args) { Node A = 先序中序后序遍历.init(); System.out.println("先序遍历"); 先序中序后序遍历.before(A); System.out.println("中序遍历"); 先序中序后序遍历.middle(A); System.out.println("后序遍历"); 先序中序后序遍历.after(A); } } class Node{ private int data; private Node leftNode; private Node rightNode; public Node(int data, Node leftNode, Node rightNode) { this.data = data; this.leftNode = leftNode; this.rightNode = rightNode; } public void setData(int data) { this.data = data; } public void setLeftNode(Node leftNode) { this.leftNode = leftNode; } public void setRightNode(Node rightNode) { this.rightNode = rightNode; } public int getData() { return data; } public Node getLeftNode() { return leftNode; } public Node getRightNode() { return rightNode; } }
回溯法:n皇后问题
n皇后问题_回溯法 - 你的雷哥 - 博客园 (cnblogs.com)
package base; import java.util.Arrays; public class n皇后问题 { private int sum = 0; private int n = 0; private int next[]; public n皇后问题(int n) { this.n = n; next = new int[n + 1]; Arrays.fill(next, 0); } public void output() { Arrays.toString(next); sum++; for (int i = 1; i <=this.n; i++) { System.out.print(next[i]); System.out.print(" "); } System.out.println(); } public boolean placeOk(int k, int next[]) { for (int i = 1; i < k; i++) { if (Math.abs(i - k) == Math.abs(next[i] - next[k]) || next[i] == next[k]) { return false; } } return true; } public void traceback(int k) { // System.out.println(k); for (int i = 1; i <= n; i++) { next[k] = i; // System.out.println(); if (placeOk(k, next)) { if (k == n) { output(); } else { traceback(k + 1); } } } } void traceback2(){ int row =1; for (int i = 1; i <=n; i++) { next[row] = i; if(placeOk(row,next)){ if(row==n){ output(); }else{ row ++; i=0; } }else{ if(i==n){ next[row] = 0; row--; i = next[row]; while (true){ if(i==n&&row!=1){ row--; i = next[row]; }else{ break; } } } } } } public static void main(String[] args) { n皇后问题 queen = new n皇后问题(4); // queen.traceback(1); queen.traceback2(); System.out.println("总共有sum=" + queen.sum + "中放置方法"); } }
无向边完全图的边数为1/2(n(n-1)),有向图的边数为n(n-1),连通分量是无向图的极大连同子图,一个连通图的生成树是一个极小连同子图
图的遍历有深度优先和广度优先两种算法:浅析几种常见算法(转载) - 你的雷哥 - 博客园 (cnblogs.com)
prim算法是求最小生成树的一种算法,具体思想是维护一个树结点集合和非树结点集合,把非树结点集合中最近的结点不断归并到树结点集合,所以一般要维护两个数组
分别是非树每个结点到树节点集合中最近距离和最近距离对应的结点和所有结点是否已经为树集合三个数组。该算法以维护结点为主,时间复杂度为结点的平方,所以适合稠密图
实现prim算法 - 你的雷哥 - 博客园 (cnblogs.com)
package base; import java.util.Arrays; import java.util.Scanner; import java.util.concurrent.ForkJoinPool; public class Prim { void Prim(int[][] Array, int n) { //定义 int lowcost[] = new int[n + 1]; //非树的结点到树的结点集合的最短路径 int cloestNode[] = new int[n + 1]; //非树结点到树结点最近的一个结点值 boolean foot[] = new boolean[n + 1]; //该节点是否已经加入到树集合中,默认为false //初始化,默认从结点一开始遍历 Arrays.fill(foot, false); foot[1] = true; for (int i = 2; i <= lowcost.length-1; i++) { lowcost[i] = Array[i][1]; cloestNode[i] = 1; } int minDistance = Integer.MAX_VALUE; //非树结点到树结点最近的距离值 int nodeNum =1; //非树结点最近的结点的编号 for (int k = 2; k <=n; k++) { //更新树 minDistance = Integer.MAX_VALUE; nodeNum = 1; for (int i = 2; i <= n; i++) { if (minDistance > lowcost[i] && foot[i] == false) { nodeNum = i; minDistance = lowcost[i]; } } foot[nodeNum] = true; System.out.println("选边" + cloestNode[nodeNum] + " " + nodeNum +" " +Array[nodeNum][cloestNode[nodeNum]]); for (int i = 2; i <= n; i++) { if (foot[i] == false && lowcost[i] > Array[i][nodeNum]){ lowcost[i] = Array[i][nodeNum]; cloestNode[i] = nodeNum; } } } } public static void main(String[] args) { Scanner scanner = new Scanner(System.in); System.out.println("请输入顶点数(从一开始)"); int node = scanner.nextInt(); System.out.println("请输入边数"); int edge = scanner.nextInt(); System.out.println("请输入边的两个结点和边权重"); int Array[][] = new int[node + 1][node + 1]; int nodeA; int nodeB; int distance; for (int i = 1; i <=node; i++) { Arrays.fill(Array[i],Integer.MAX_VALUE); } for (int i = 0; i < edge; i++) { nodeA = scanner.nextInt(); nodeB = scanner.nextInt(); distance = scanner.nextInt(); Array[nodeA][nodeB] = distance; Array[nodeB][nodeA] = distance; } Prim prim = new Prim(); prim.Prim(Array, node); } } /* 1 2 6 1 3 1 1 4 5 2 5 3 2 3 5 3 5 6 3 6 4 3 4 4 4 6 2 5 6 6 * */ //https://www.cnblogs.com/henuliulei/p/9951778.html
第二种求最小生成树的算法是克鲁斯卡尔算法
该算法是维护所有的边,从最小的边开始维护,把边具有不同颜色的归并到一种颜色(比如较小值的结点的颜色),注意如果边的两个结点颜色相同,说明这个边已经处以同一个连通分量,此时应该拒绝归并,初始时所有的结点都对应不同的连通分量,该算法要维护一个颜色数组,把边的两个结点和边的长度可以组成一个字符串来维护,而且好根据边长进行排序。时间复杂度为eloge,因为维护边,所以适合边少的图,也就是稀疏图。
最小生成树的Kruskal算法 - wxdjss - 博客园 (cnblogs.com)
package base; import java.util.Arrays; import java.util.Scanner; public class Kruskal { void kru(String Array[], int edge, int color[]) { int distance = 0; int nodeA = 0; int nodeB = 0; for (int i = 1; i <= Array.length - 1; i++) { distance = Integer.parseInt(Array[i].substring(0, 1)); nodeA = Integer.parseInt(Array[i].substring(1, 2)); nodeB = Integer.parseInt(Array[i].substring(2, 3)); if (color[nodeA] != color[nodeB]) { //把连在一起的边设置成相同的颜色 System.out.println("把边" + nodeA + nodeB + "划进来"); for (int j = 1; j <=color.length-1; j++) { if(color[j] == color[nodeB] && j!=nodeB){ color[j] = color[nodeA]; } } color[nodeB] = color[nodeA]; } } } public static void main(String[] args) { Scanner scanner = new Scanner(System.in); System.out.println("请输入顶点数(从一开始)"); int node = scanner.nextInt(); System.out.println("请输入边数"); int edge = scanner.nextInt(); System.out.println("请输入边的两个结点和边权重"); // int Array[][] = new int[node + 1][node + 1]; int nodeA; int nodeB; int distance; String[] Array = new String[edge + 1]; Array[0] = "000"; for (int i = 1; i <= edge; i++) { nodeA = scanner.nextInt(); nodeB = scanner.nextInt(); if (nodeA > nodeB) { int temp = nodeA; nodeA = nodeB; nodeB = temp; } distance = scanner.nextInt(); Array[i] = distance + "" + nodeA + "" + nodeB; } Arrays.sort(Array); System.out.println(Arrays.toString(Array)); //初始化颜色标记 int color[] = new int[node + 1]; for (int i = 0; i < node; i++) { color[i + 1] = i + 1; //开始颜色都不一样,代表不同的连通分量 } Kruskal kruskal = new Kruskal(); kruskal.kru(Array, edge, color); } }
迪杰斯特拉算法是求最短路径 的算法,时间复杂度为0(n^2),该算法和prim算法很相似,也是归并顶点,把路径最短的非树结点归并进来,同时进行更新其他结点,其他结点判断和新节点的距离+新节点本身的路径长度与原来最短路径长度对比,如果经过新节点的路径更短则更新这个最短路径和最短距离的路径。
维护的数组和prim相似,一个是否为已经归并的结点,一个最短路径的距离的数组,一个最短距离对应的路径,每轮循环获取一个最短路径的结点归并并根据这个新节点动态新其他非归并结点的最短路径和距离即可,和prim的区别是一个是维护最短路径,一个是和归并结点集合的最进一个结点的距离的数组。
代码实现思路几乎一致 。实现迪杰斯特拉算法 - 你的雷哥 - 博客园 (cnblogs.com)
package base; import java.util.Arrays; import java.util.Scanner; public class Dijkstra { public void dij(int Array[][], int node) { //定义 int cloest[] = new int[node + 1]; //计算非树结点到树起始结点的最短距离,维护进行实时更新。 boolean foot[] = new boolean[node + 1]; //标注该结点是不是已经计算出最短路径的结点了 String[] path = new String[node + 1]; //考虑使用字符串记录路径 //初始化 Arrays.fill(foot, false); foot[1] = true; //从结点1开始 cloest[1] = 0; //自己到自己的距离为0 Arrays.fill(path, ""); for (int i = 2; i <= cloest.length - 1; i++) { cloest[i] = Array[1][i]; //初始各个结点从1出发的最短距离 if (cloest[i] != Integer.MAX_VALUE) { path[i] = "" + 1; } else { path[i] = ""; } } int newNode = 1; //该变量维护新加进的结点 //更新 for (int i = 2; i <= Array.length - 1; i++) { int minDis = Integer.MAX_VALUE; for (int j = 2; j <= Array.length - 1; j++) { if (minDis > cloest[j] && foot[j] == false) { minDis = cloest[j]; newNode = j; } } foot[newNode] = true; path[newNode] = path[newNode] + " " + newNode; System.out.println(String.format("从出发结点到结点%d的最短距离为%d,路径为:%s",newNode,minDis,path[newNode])); for (int j = 2; j <= Array.length - 1; j++) { if (Array[newNode][j]+cloest[newNode] < cloest[j] && foot[j] == false) { cloest[j] = Array[newNode][j] + cloest[newNode]; path[j] = path[newNode]; } } } } public static void main(String[] args) { Scanner scanner = new Scanner(System.in); System.out.println("请输入顶点数(从一开始)"); int node = scanner.nextInt(); System.out.println("请输入边数"); int edge = scanner.nextInt(); System.out.println("请输入边的两个结点和边权重"); int Array[][] = new int[node + 1][node + 1]; int nodeA; int nodeB; int distance; for (int i = 1; i <= node; i++) { Arrays.fill(Array[i], 999999); //一个较大的数字,该数字要保证大于测试用例的最大值,注意不能过大或者接近int上限 } for (int i = 0; i < edge; i++) { nodeA = scanner.nextInt(); nodeB = scanner.nextInt(); distance = scanner.nextInt(); Array[nodeA][nodeB] = distance; Array[nodeB][nodeA] = distance; } new Dijkstra().dij(Array,node); } } /* 1 2 10 1 5 100 2 3 50 4 3 20 4 5 60 3 5 10 1 4 30 */
折半查找(二分查找),注意当查找的树小于mid,应该把end = mid-1,大于mid则begin = mid+1,结束条件是begin > end
package base; import java.util.Arrays; import java.util.Map; import java.util.Scanner; //https://blog.csdn.net/zs_66666/article/details/89463029 public class BinarySearch { //折半查找,又称二分查找 void binarySerach(int num,int Array[], int len) { //查找终止的条件是begin > end int begin = 0; int end = len - 1; int mid = (int) Math.floor((double) (begin + end)/2.0); while (begin <= end){ if(Array[mid]==num){ System.out.println("find num,the index is mid="+mid); break; } if(Array[mid]>num){ end = mid - 1; } if(Array[mid] < num){ begin = mid + 1; } mid = (int) Math.floor((double) (begin + end)/2.0); } if(begin > end){ System.out.println("not found ,find over"); } } public static void main(String[] args) { int Array[] = {3, 1, 10, 12, 17, 19, 23, 27, 31, 37}; Arrays.sort(Array); System.out.println(Arrays.toString(Array)); Scanner scanner = new Scanner(System.in); int num = scanner.nextInt(); new BinarySearch().binarySerach(num,Array, Array.length); } } /* 索引顺序表是建立一个小的索引,该顺序表的特点是把表分成几份,每份的最小值大于前一份的最大值,内部可以无序,此时只需要根据数据的大小就可以判断该数在哪个小区间里面 然后在小区间里面进行顺序查找或者使用其他方法加快小区间的查找速度。 */
索引顺序表

二叉排序树的插入和查找,和删除
二叉排序树(二叉查找树)及C语言实现 (biancheng.net)
查找使用中序遍历,插入直接在判定大小后在指定位置插入元素即可,删除元素,原理类似,找到元素,把该处设置为null,存在一个孩子,直接孩子替换父亲,孩子删除。存在两个孩子,左孩子替代自己,右孩子放在左孩子的最大值处(也就是前驱结点)
package base; /** * 构建一棵二叉排序树 * 对树进行遍历查找元素, * 找到树的最大值,找到树的最小值 * 添加元素(如果存在该元素直接返回,否则在叶子结点的左孩子或者右孩子插入) * 删除元素思想(如果该元素没有孩子,直接删除,如果有左孩子或者右孩子,孩子直接替换父亲,如果元素左右孩子都有,可以把左孩子替换自己,右孩子放到自己的直接前驱,并删除右孩子 * 反之亦然) */ //构建一棵树 class BinTree{ private int data; private BinTree left; private BinTree right; public BinTree(int data, BinTree left, BinTree right) { this.data = data; this.left = left; this.right = right; } public BinTree(int data) { super(); this.data = data; } public int getData() { return data; } public BinTree getLeft() { return left; } public BinTree getRight() { return right; } public void setData(int data) { this.data = data; } public void setLeft(BinTree left) { this.left = left; } public void setRight(BinTree right) { this.right = right; } @Override public String toString() { return "BinTree{" + "data=" + data + '}'; } } public class BinarySearch2 { static int num = 0; private BinTree root; public BinarySearch2(BinTree root) { this.root = root; } public BinarySearch2() { } public BinTree getRoot() { return root; } public void setRoot(BinTree root) { this.root = root; } //实现前序查找 public void frontFind(BinTree node,int searchNum){ if(node == null){ }else{ if(searchNum == node.getData()){ num = 1; // System.out.println("find the num"); }else if(searchNum > node.getData()){ if(num == 0 ){ frontFind(node.getRight(),searchNum); } }else{ if(num ==0){ frontFind(node.getLeft(),searchNum); } } } } //找到树的最大值 public BinTree findTreeMaxValue(BinTree binTree){ if(binTree != null){ if(binTree.getRight()==null){ System.out.println(binTree.getData()); return binTree; } else{ BinTree temp = new BinTree(0); while (true){ BinTree right = binTree.getRight(); if(right.getRight()==null){ System.out.println(right.getData()); temp = binTree; break; }else{ binTree = right; continue; } } return temp; } } return null; } //找到树的最小值 public void findTreeMinValue(BinTree binTree){ if(binTree != null){ if(binTree.getLeft()==null){ System.out.println(binTree.getData()); } else{ while (true){ BinTree left = binTree.getLeft(); if(left.getLeft()==null){ System.out.println(left.getData()); break; }else{ binTree = left; continue; } } } } } //添加元素 public void add(BinTree binTree, int num){ if(binTree != null){ if(binTree.getData() == num){ System.out.println("插入失败,已经存在该元素"); } if(binTree.getData() < num){ if(binTree.getRight() == null){ binTree.setRight(new BinTree(num)); System.out.println("插入成功,在元素" + binTree.getData() + "右孩子处"); }else{ add(binTree.getRight(),num); } }else{ if(binTree.getLeft() == null){ binTree.setLeft(new BinTree(num)); System.out.println("插入成功,在元素" + binTree.getData() + "左孩子处"); }else{ add(binTree.getLeft(),num); } } } } //删除元素,原理类似,找到元素,把该处设置为null,存在一个孩子,直接孩子替换父亲,孩子删除。存在两个孩子,左孩子替代自己,右孩子放在左孩子的最大值处(也就是前驱结点) public void delete(BinTree binTree, int num){ if(binTree != null){ if(binTree.getData() == num){ if(binTree.getLeft()==null && binTree.getRight()==null){ System.out.println("删除了元素" + binTree.getData()); binTree = null; //没有孩子直接删除 }else if(binTree.getRight()==null&& binTree.getLeft()!=null){ //有一个左孩子 BinTree temp = new BinTree(0); temp = binTree.getLeft(); System.out.println("删除了元素" + binTree.getData()); binTree = temp; temp = null; }else if(binTree.getLeft()==null&& binTree.getRight()!=null){ //有一个右孩子 BinTree temp = new BinTree(0); temp = binTree.getRight(); System.out.println("删除了元素" + binTree.getData()); binTree = temp; temp = null; }else{ //有两个孩子 BinTree temp = new BinTree(0); temp = binTree.getRight(); //右孩子 BinTree temp1 = findTreeMaxValue(binTree); //前驱结点 temp1.setRight(temp); //把右孩子指向前驱结点 binTree.setRight(null); //删除右孩子 System.out.println(temp); binTree = binTree.getLeft(); //删除元素 System.out.println(binTree); } } else if(binTree.getData() < num){ if(binTree.getRight() == null){ System.out.println("没有找到元素,删除失败"); }else{ delete(binTree.getRight(),num); } }else{ if(binTree.getLeft() == null){ System.out.println("没有找到元素,删除失败"); }else{ delete(binTree.getLeft(),num); } } } } //构建树,并进行查找元素 public static void main(String[] args) { BinTree node2 = new BinTree(2, null, null); BinTree node4 = new BinTree(4, null, null); BinTree node8 = new BinTree(8, null, null); BinTree node1 = new BinTree(1, null, node2); BinTree node5 = new BinTree(5, node4, null); BinTree node7 = new BinTree(7, null, node8); BinTree node3 = new BinTree(3, node1, node5); BinTree node9 = new BinTree(9, node7, null); BinTree node6 = new BinTree(6, node3, node9); BinarySearch2 binarySearch2 = new BinarySearch2(); binarySearch2.frontFind(node6,10); System.out.println(num); binarySearch2.findTreeMaxValue(node3); binarySearch2.findTreeMinValue(node9); binarySearch2.add(node6,10); binarySearch2.delete(node6,6); } }
二叉排序树很对情况下不是平衡的,而平衡二叉树则根据不同的书的定义有不同的答案关于是否为二叉排序树
平衡二叉树,四种情况
平衡二叉排序树|AVL树-从入门到入土-全网最详细的教程-自带金手指秘技【国王、小弟。。。还有腰间盘同学的爱恨情仇】_哔哩哔哩_bilibili
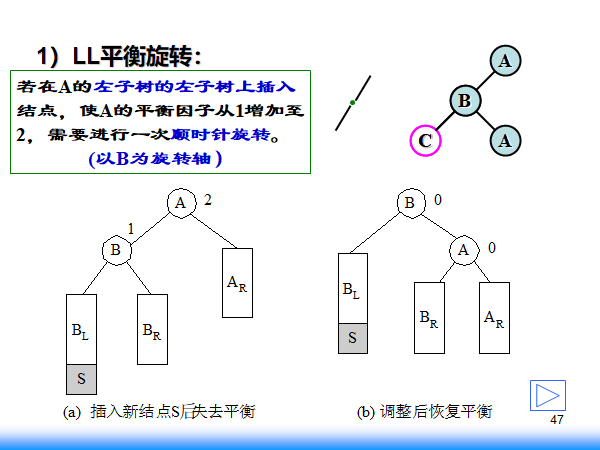
左孩子的左孩子为失衡点,包括右孩子的左孩子本身的存在(此时没有右孩子)或者在左孩子的左孩子上插入了新结点使得失衡,此时需要右转
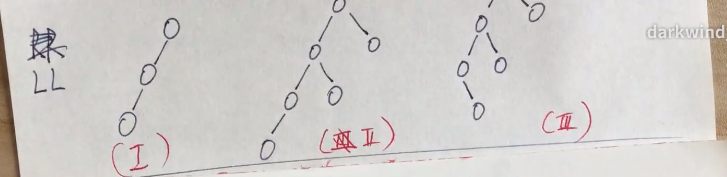
注意第二种或第三种情况此时右转需要鸠占鹊巢,左孩子的右孩子要被替换掉,因为该节点小于父节点所以要放在其左孩子。其他情况类似。

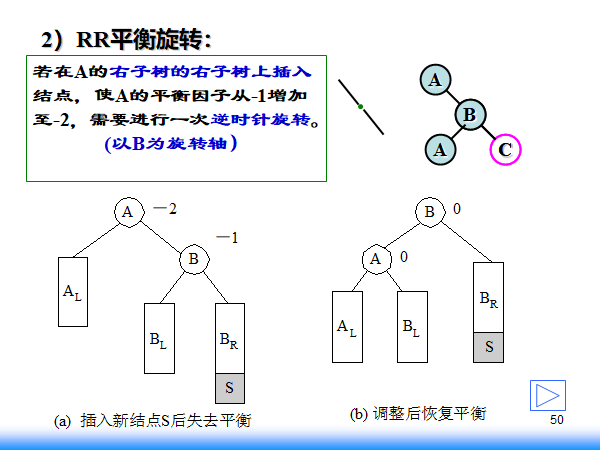
右孩子的右孩子为失衡点,包括右孩子的右孩子本身的存在(此时没有左孩子)或者在右孩子的右孩子上插入了新结点使得失衡,此时需要左转,那么父节点就可能占用
右孩子的左孩子的位置,并根据大小进行确定被占孩子的位置。
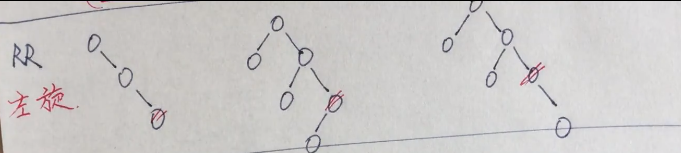
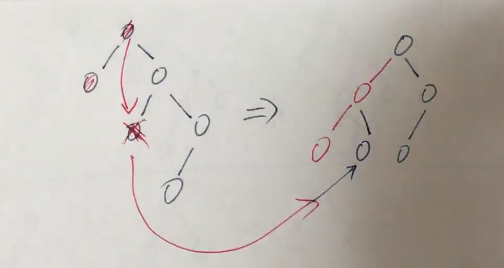

左孩子的右孩子为失衡点,包括左孩子的右孩子本身的存在(此时没有左孩子)或者在左孩子的右孩子上插入了新结点使得失衡,此时需要先左转再右转,同时会存在鸠占鹊巢,同时注意丢锅问题,


二叉堆的调整
/**
* 构建一棵二叉排序树
* 对树进行遍历查找元素,
* 找到树的最大值(不断获取右孩子就可以),找到树的最小值(不断获取左孩子就可以)
* 添加元素(如果存在该元素直接返回,否则在叶子结点的左孩子或者右孩子插入)
* 删除元素思想(如果该元素没有孩子,直接删除,如果有左孩子或者右孩子,孩子直接替换父亲,如果元素左右孩子都有,可以把左孩子替换自己,右孩子放到自己的直接前驱,并删除右孩子
* 反之亦然)
*/
package base; /** * 构建一棵二叉排序树 * 对树进行遍历查找元素, * 找到树的最大值(不断获取右孩子就可以),找到树的最小值(不断获取左孩子就可以) * 添加元素(如果存在该元素直接返回,否则在叶子结点的左孩子或者右孩子插入) * 删除元素思想(如果该元素没有孩子,直接删除,如果有左孩子或者右孩子,孩子直接替换父亲,如果元素左右孩子都有,可以把左孩子替换自己,右孩子放到自己的直接前驱,并删除右孩子 * 反之亦然) */ //构建一棵树 class BinTree{ private int data; private BinTree left; private BinTree right; public BinTree(int data, BinTree left, BinTree right) { this.data = data; this.left = left; this.right = right; } public BinTree(int data) { super(); this.data = data; } public int getData() { return data; } public BinTree getLeft() { return left; } public BinTree getRight() { return right; } public void setData(int data) { this.data = data; } public void setLeft(BinTree left) { this.left = left; } public void setRight(BinTree right) { this.right = right; } @Override public String toString() { return "BinTree{" + "data=" + data + '}'; } } public class BinarySearch2 { static int num = 0; private BinTree root; public BinarySearch2(BinTree root) { this.root = root; } public BinarySearch2() { } public BinTree getRoot() { return root; } public void setRoot(BinTree root) { this.root = root; } //实现前序查找 public void frontFind(BinTree node,int searchNum){ if(node == null){ }else{ if(searchNum == node.getData()){ num = 1; // System.out.println("find the num"); }else if(searchNum > node.getData()){ if(num == 0 ){ frontFind(node.getRight(),searchNum); } }else{ if(num ==0){ frontFind(node.getLeft(),searchNum); } } } } //找到树的最大值 public BinTree findTreeMaxValue(BinTree binTree){ if(binTree != null){ if(binTree.getRight()==null){ System.out.println(binTree.getData()); return binTree; } else{ BinTree temp = new BinTree(0); while (true){ BinTree right = binTree.getRight(); if(right.getRight()==null){ System.out.println(right.getData()); temp = binTree; break; }else{ binTree = right; continue; } } return temp; } } return null; } //找到树的最小值 public void findTreeMinValue(BinTree binTree){ if(binTree != null){ if(binTree.getLeft()==null){ System.out.println(binTree.getData()); } else{ while (true){ BinTree left = binTree.getLeft(); if(left.getLeft()==null){ System.out.println(left.getData()); break; }else{ binTree = left; continue; } } } } } //添加元素 public void add(BinTree binTree, int num){ if(binTree != null){ if(binTree.getData() == num){ System.out.println("插入失败,已经存在该元素"); } if(binTree.getData() < num){ if(binTree.getRight() == null){ binTree.setRight(new BinTree(num)); System.out.println("插入成功,在元素" + binTree.getData() + "右孩子处"); }else{ add(binTree.getRight(),num); } }else{ if(binTree.getLeft() == null){ binTree.setLeft(new BinTree(num)); System.out.println("插入成功,在元素" + binTree.getData() + "左孩子处"); }else{ add(binTree.getLeft(),num); } } } } //删除元素,原理类似,找到元素,把该处设置为null,存在一个孩子,直接孩子替换父亲,孩子删除。存在两个孩子,左孩子替代自己,右孩子放在左孩子的最大值处(也就是前驱结点) public void delete(BinTree binTree, int num){ if(binTree != null){ if(binTree.getData() == num){ if(binTree.getLeft()==null && binTree.getRight()==null){ System.out.println("删除了元素" + binTree.getData()); binTree = null; //没有孩子直接删除 }else if(binTree.getRight()==null&& binTree.getLeft()!=null){ //有一个左孩子 BinTree temp = new BinTree(0); temp = binTree.getLeft(); System.out.println("删除了元素" + binTree.getData()); binTree = temp; temp = null; }else if(binTree.getLeft()==null&& binTree.getRight()!=null){ //有一个右孩子 BinTree temp = new BinTree(0); temp = binTree.getRight(); System.out.println("删除了元素" + binTree.getData()); binTree = temp; temp = null; }else{ //有两个孩子 BinTree temp = new BinTree(0); temp = binTree.getRight(); //右孩子 BinTree temp1 = findTreeMaxValue(binTree); //前驱结点 temp1.setRight(temp); //把右孩子指向前驱结点 binTree.setRight(null); //删除右孩子 System.out.println(temp); binTree = binTree.getLeft(); //删除元素 System.out.println(binTree); } } else if(binTree.getData() < num){ if(binTree.getRight() == null){ System.out.println("没有找到元素,删除失败"); }else{ delete(binTree.getRight(),num); } }else{ if(binTree.getLeft() == null){ System.out.println("没有找到元素,删除失败"); }else{ delete(binTree.getLeft(),num); } } } } //构建树,并进行查找元素 public static void main(String[] args) { BinTree node2 = new BinTree(2, null, null); BinTree node4 = new BinTree(4, null, null); BinTree node8 = new BinTree(8, null, null); BinTree node1 = new BinTree(1, null, node2); BinTree node5 = new BinTree(5, node4, null); BinTree node7 = new BinTree(7, null, node8); BinTree node3 = new BinTree(3, node1, node5); BinTree node9 = new BinTree(9, node7, null); BinTree node6 = new BinTree(6, node3, node9); BinarySearch2 binarySearch2 = new BinarySearch2(); binarySearch2.frontFind(node6,10); System.out.println(num); binarySearch2.findTreeMaxValue(node3); binarySearch2.findTreeMinValue(node9); binarySearch2.add(node6,10); binarySearch2.delete(node6,6); } }
B+树B-树,红黑树
hash函数构造方法、
(1)直接定址法:取关键字或关键字的某个线性函数值为hash地址 H(key) = key或 H(key) = a.key+b
(2)数字分析法:取关键字的若干位组成hash地址:一般这几位最能保证数据分布的均匀
(3)平方取中法:取关键字平方后的中间几位为hash地址
(4)除留取余法:除不超过数组长的余数作为地址
(5)随机数法
解决冲突
(1)再hash
(2)开放定址法(随机线性再散列,二次线性再散列,再hash法,链地址法),
(3)链地址法
(4),建立一个公共溢出缓冲区
排序

主要是记住算法的思想,之后代码很容易实现,重点关注快排和堆排序和归并排序的原理和代码,其中希尔排序,选择排序,快排和堆排序是不稳定的排序算法。希尔和桶的三个算法是o(n),快排,堆,归并是nlog
基数排序 - 如果天空不死 - 博客园 (cnblogs.com)(凑位数,按照位数排序)
(1条消息) 基数排序、桶排序和计数排序的区别_Rnan_wang的博客-CSDN博客 (计数排序最简单,下标就是数,桶排序按照区间放数据,内部要使用任意排序算法再次排序。基数排序则是根据位数放桶,从低到高,放多轮完成排序)
12中排序的思想
12种排序算法(转载) - 你的雷哥 - 博客园 (cnblogs.com)
按照思想自己实现的代码,可能代码不够简洁、
package base; import java.util.Arrays; public class Sort { //从第二个元素开始从后向前和前面元素一一比较,当该元素大于等于前一个或者处于第一个位置,并小于等于 //后一个或者处于最后一个位置,则在该位置插入,后面已排序元素后移,以此完成所有元素的排序 public void straightInsertionSort(int Array[]){ //直接插入排序 for (int i = 1; i < Array.length; i++) { int index = i; for (int j = i-1; j >=0; j--) { if(Array[j] > Array[index]){ int temp = Array[index]; Array[index] = Array[j]; Array[j] = temp; index = j; }else{ break; } } } System.out.println(Arrays.toString(Array)); } //二分插入排序:在要进行插入的元素在前面已排序元素中进行二分查找插入位置 void binaryInsertSort(int Array[]) { for (int i = 1; i < Array.length; i++) { int index = i; int begin = 0; int end = i - 1; int mid = (begin + end) / 2; while (true) { if (Array[end] <= Array[index]) { int temp = Array[i]; for (int j = i - 1; j >= end + 1; j--) { Array[j + 1] = Array[j]; } Array[end] = temp; break; } if (begin == end - 1 && Array[begin] <= Array[index] && Array[index] <= Array[end]) { int temp = Array[i]; for (int j = i - 1; j >= end; j--) { Array[j + 1] = Array[j]; } Array[end] = temp; break; } if (Array[index] < Array[begin]) { int temp = Array[i]; for (int j = i - 1; j >= begin; j--) { Array[j + 1] = Array[j]; } Array[begin] = temp; } if (Array[index] > Array[mid]) { begin = mid + 1; mid = (begin + end) / 2; } else { end = mid - 1; mid = (begin + end) / 2; } if (begin > end) { break; } } } System.out.println(Arrays.toString(Array)); } //希尔排序,在增量对位之间比较排序,并不断减少增量来进行排序,最终达到所有数据有序 void shellSort(int Array[]) { int icr = Array.length - 1; while (true) { for (int i = 0; i < Array.length; i++) { int index = i + icr; if (index >= Array.length) { break; } if (Array[index] <= Array[i]) { int temp = Array[index]; Array[index] = Array[i]; Array[i] = temp; } } icr--; if (icr == 0) { break; } } System.out.println(Arrays.toString(Array)); } //选择排序,每一轮选择最小的值放在未排序的第一个位置,然后作为已排序 public void chooseSort(int Array[]) { for (int i = 0; i < Array.length - 1; i++) { int min = Integer.MAX_VALUE; //假设待排序数字不超过min int begin = Array[i]; int index = i; for (int j = i; j < Array.length; j++) { if (Array[j] < min) { min = Array[j]; index = j; } } int temp = Array[i]; Array[i] = Array[index]; Array[index] = temp; } System.out.println(Arrays.toString(Array)); } //冒泡排序,每一次排序进行交换,最大的值一定被交换到最低端 public void maopoSort(int Array[]) { for (int i = 0; i < Array.length; i++) { for (int j = 0; j < Array.length - i - 1; j++) { if (Array[j] > Array[j + 1]) { int temp = Array[j]; Array[j] = Array[j + 1]; Array[j + 1] = temp; } } } System.out.println(Arrays.toString(Array)); } //鸡尾酒排序,双向冒泡排序,先沉底得到最大值,再反过来获取最小值,也就是一轮排好两个数据 public void chickenSort(int Array[]) { int begin = 0; int end = Array.length - 1; while (true) { for (int i = begin; i < end; i++) { if (Array[i] > Array[i + 1]) { int temp = Array[i]; Array[i] = Array[i + 1]; Array[i + 1] = temp; } } end = end - 1; for (int i = end - 1; i >= begin + 1; i--) { if (Array[i] < Array[i - 1]) { int temp = Array[i]; Array[i] = Array[i - 1]; Array[i - 1] = temp; } } begin = begin + 1; if (begin >= end) { break; } } System.out.println(Arrays.toString(Array)); } //快速排序,实现思想是,一般选取区间的第一个元素作为中心点pivot,然后选pivot元素和区间最后一个元素的位置 //作为两个索引指针,先从第二个索引指针指向的最后一个元素开始比较,如果小于pivot则把元素移到第一个指针,第一个指针右移, //然后把第一个指针指向的新元素和pivot比较,大于则移到到第二个指针的位置,第二个指针左移,以此类推,当第一个指针和第二个指针 //相等一轮排序完成,把pivot的值移到指针指向的这个元素。然后递归的pivot两边的区间进行排序 public void quickSort(int Array[], int lefts, int ends, int pivot) { int left = lefts; int end = ends; int num = Array[pivot]; if (left >= end) return; while (true) { while (true) { if (Array[end] < num) { Array[left] = Array[end]; left++; break; } else { if (end > left) { end--; } else { break; } } } if (end <= left) { break; } while (true) { if (Array[left] > num) { Array[end] = Array[left]; end--; break; } else { if (left < end) { left++; } else { break; } } } if (end <= left) { break; } } Array[left] = num; quickSort(Array, lefts, left - 1, lefts); quickSort(Array, left + 1, ends, end + 1); } //堆排序,把数组变成一个完全二叉树形式的堆,数组的第n个位置(一把起始位置设置为1)的孩子是2n和2n+1,那么反过来n和n+1的孩子就是 //n/2,我们从叶子节点开始,n/2后面都是叶子节点,n为元素的个数,数组起始值为1,比双亲节点小的替换,这样一轮排序可以把根节点变为最小值 //或者最大值,把根节点设置为数组的最后一个值,之后在对前n-1个数据进行相同的操作即可。从小到大排序推荐使用大顶推 public void heapSort(int Array[]) { int times = Array.length - 1; while (true) { for (int i = times; i > 0; i--) { if (Array[i] > Array[i / 2]) { int temp = Array[i]; Array[i] = Array[i / 2]; Array[i / 2] = temp; } } int temp = Array[0]; Array[0] = Array[times]; Array[times] = temp; if (times == 0) { break; } times--; } System.out.println(Arrays.toString(Array)); } //归并排序,思想是先把数组不断分治的分成小份,当分成只剩一个元素时是停止条件,分好之后,在把相邻的两个区间begin到mid和mid到 //end之间的元素进行合并,合并就是两个区间从头到尾遍历,哪个小先放进一个新的数组里面,最新排好在重写写回原来的数组 //这样不断合并实现最终的排序,所以需要两个函数,一个合并函数,一个分治的拆分函数 public void mergeAdd(int Array[], int begin, int mid, int end) { int i = begin; int j = mid+1; int temp[] = new int[end - begin + 1]; int index = 0; while (i<=mid && j<=end) { if (Array[i] <= Array[j]) { temp[index++] = Array[i++]; } else{ temp[index++] = Array[j++]; } } for (; i <=mid; i++) { temp[index++] = Array[i]; } for (; j <= end; j++) { temp[index++] = Array[j]; } // System.out.println(Arrays.toString(temp)); // System.out.println(index == end-begin+1); for (int k = begin; k <=end; k++) { Array[k] = temp[k-begin]; } } public void mergeSort(int Array[], int begin, int end) { if (begin < end) { int middle = (begin + end) / 2; mergeSort(Array, begin, middle); mergeSort(Array, middle+1, end); mergeAdd(Array, begin, middle,end); } } //计数排序,计数排序的思想就是把数据放在一个个数据单元里面,也就是放在一个新的数组里面,数据的值刚好等于新数组的下标,每放进一个相同的值 //同一个桶的值加一,注意初始所有的桶的值为0,放一个加一 //那么遍历新数组时,如果该数组不为零,就删除下标值,并且桶里面有几个值就输出几次,值得注意的是,桶的初始大小取决于数组的最大值。 public void countSort(int Array[]){ int maxValue = -999999; for (int i = 0; i < Array.length; i++) { if(maxValue < Array[i]){ maxValue = Array[i]; } } int bucket[] = new int[maxValue+1]; Arrays.fill(bucket,0); for (int i = 0; i < Array.length; i++) { bucket[Array[i]] +=1; } int index = 0; int bucketIndex = 0; while (true){ if(index >= Array.length){ break; } int value = bucket[bucketIndex]; for (int i = 0; i < value; i++) { Array[index++] = bucketIndex; } bucketIndex ++; } System.out.println(Arrays.toString(Array)); } //桶排序:思想是把数据在最大值和最小值划分成指定相等的区间,把位于该区间的数放在桶里面,在利用其它排序算法进行桶内的排序。 //考虑测试数据无负数 public void bucketSort(int Array[]){ int maxValue = Integer.MIN_VALUE; for (int i = 0; i < Array.length; i++) { //获取最大值方便划分桶区间 if(Array[i] > maxValue){ maxValue = Array[i]; } } int bucketNum = maxValue/10; //每个桶存的数的区间是10范围。 int bucket[][] = new int[bucketNum + 1][100]; //假设每个区间的数不超过100个,根据实际情况确定该数值 for (int i = 0; i < bucketNum+1; i++) { Arrays.fill(bucket[i],Integer.MAX_VALUE); //小于int最大值的就是桶里面放的数组 } int indexNum[] = new int[bucketNum+1]; //该数组是统计桶里面放的数据的个数 Arrays.fill(indexNum,0); for (int i = 0; i < Array.length; i++) { //把数放在对应的桶里面 bucket[Array[i]/10][indexNum[Array[i]/10]++] = Array[i]; } //对每个桶内的数据进行排序,因为数据分散了,每个桶内排序时间上大大降低 int num = 0; while (true){ if(num > bucketNum) break; for (int i = 0; i < indexNum[num]-1; i++) { //对每个桶排序,冒泡 for (int j = 0; j < indexNum[num]-1-i; j++) { if(Array[j] > Array[j+1]){ int temp = Array[j]; Array[j] = Array[j+1]; Array[j+1]= temp; } } } num ++; } int index = 0; for (int i = 0; i < bucketNum+1; i++) { //从小到大赋值 for (int j = 0; j < indexNum[i]; j++) { Array[index++] = bucket[i][j]; } } System.out.println(Arrays.toString(Array)); } //基数排序,思路是把把所有的数字的位数设置一致,都是最大值得位数,不足的不零。 //然后从最低位开始放到对应桶里面,实现按照最低位排序,然后依次排序更高位,最终实现所有位的排序 //实现最终排序效果,由于考虑到按照数位排序,所以可以把数组的值设置为字符串 public void jishuSort(int Array[]){ String str[] = new String[Array.length]; for (int i = 0; i < Array.length; i++) { //先把数组改为字符数组 str[i] = String.valueOf(Array[i]); } int maxLength=1; //获取最大的位数 for (int i = 0; i < str.length; i++) { if(str[i].length()>maxLength){ maxLength = str[i].length(); } } for (int i = 0; i < str.length; i++) { //为不满足位数的补零 // System.out.println(str[i].length()); int tempLength = str[i].length(); for (int j = 0; j <maxLength-tempLength; j++) { str[i] = "0"+str[i]; } } //把数据放到桶里面,从低位开始 int bucket[][] = new int[10][100]; //每个桶最多放100个元素,根据实际情况声明 for (int i = 0; i < bucket.length; i++) { Arrays.fill(bucket[i],Integer.MAX_VALUE); } int bucketIndexNum[] = new int[10]; //用来统计每个桶放的元素的个数 int numCount = 0; //记录数位,从个位开始 while (true){ //开始放数据,从低位开始,while一直等到低位到高位放过一轮结束 if(numCount >= maxLength) break; Arrays.fill(bucketIndexNum,0); for (int i = 0; i < str.length; i++) { //放到桶里面 int num = Integer.parseInt(str[i].substring(maxLength-numCount-1,maxLength-numCount));//获取指定位的数字 bucket[num][bucketIndexNum[num]++] = Integer.parseInt(str[i]); } //取出按指定位数排序后的数据再放到数组里面 int index = 0; for (int i = 0; i < 10; i++) { for (int j = 0; j < bucketIndexNum[i]; j++) { str[index++] = String.valueOf(bucket[i][j]); } } for (int i = 0; i < str.length; i++) { //重新补零 // System.out.println(str[i].length()); int tempLength = str[i].length(); for (int j = 0; j <maxLength-tempLength; j++) { str[i] = "0"+str[i]; } } numCount ++; } //完成排序,取出数据 for (int i = 0; i < Array.length; i++) { Array[i] = Integer.parseInt(str[i]); } System.out.println(Arrays.toString(Array)); } public static void main(String[] args) { Sort sort = new Sort(); int Array[] = {111, 222, 32, 11, 2, 11, 123, 21, 112, 1000}; // sort.binaryInsertSort(Array); // sort.shellSort(Array); // sort.chooseSort(Array); // sort.maopoSort(Array); // sort.chickenSort(Array); // sort.quickSort(Array, 0, Array.length - 1, 0); // System.out.println(Arrays.toString(Array)); // sort.heapSort(Array); // sort.mergeSort(Array,0,Array.length-1); // System.out.println(Arrays.toString(Array)); // sort.countSort(Array); // sort.bucketSort(Array); sort.jishuSort(Array); } }