标准方程法_岭回归_LASSO算法_弹性网

程序所用文件：https://files.cnblogs.com/files/henuliulei/%E5%9B%9E%E5%BD%92%E5%88%86%E7%B1%BB%E6%95%B0%E6%8D%AE.zip

标准方程法

标准方程法是求取参数的另一种方法，不需要像梯度下降法一样进行迭代，可以直接进行结果求取

 那么参数W如何求，下面是具体的推导过程

 

 

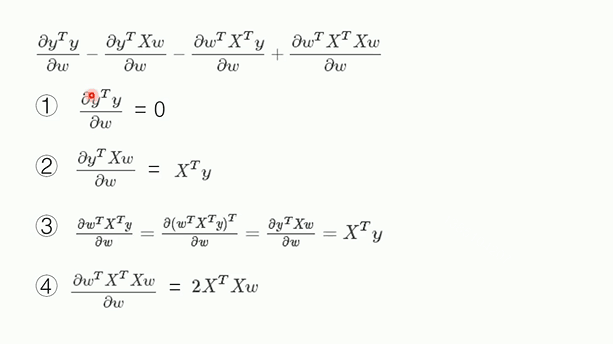
 因此参数W可以根据最后一个式子直接求取，但是我们知道，矩阵如果线性相关，那么就无法取逆，如下图

 因此，对比梯度下降法和标准方程法我们可以得到下面的图

 下面的demo是标准方程法实现拟合

import numpy as np
from matplotlib import pyplot as plt
from numpy import genfromtxt
#载入数据
data = genfromtxt('data.csv',delimiter=',')
x_data = data[:,0,np.newaxis]#一维变为二维
y_data = data[:,1,np.newaxis]
plt.scatter(x_data,y_data)
plt.show()
print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
#给样本添加偏置项
X_data = np.concatenate((np.ones((100,1)),x_data),axis=1)
print(X_data.shape)
#标准方程法求解回归参数
def weights(xArr, yArr):
    xMat = np.mat(xArr)#array变为mat,方便进行矩阵运算
    yMat = np.mat(yArr)
    xTx = xMat.T * xMat
    if np.linalg.det(xTx) == 0.0:   #一、np.linalg.det():矩阵求行列式二、np.linalg.inv()：矩阵求逆三、np.linalg.norm():求范数
        print("该矩阵不可逆")
        return
    ws = xTx.I * xMat.T * yMat
    return  ws
ws = weights(X_data,y_data)
print(ws[1].shape)
#画图
x_test = np.array([[20], [80]])
print(x_test.shape)
y_test = ws[0] +  x_test * ws[1]
plt.plot(x_data, y_data, 'b.')
plt.plot(x_test, y_test, 'r')
plt.show()

捎带一下两个小的知识点

数据归一化

由于单位的原因，不同单位之间数据产别太大，影响数据分析，所以我们一般会对某些数据进行归一化，即把数据归一化到某个范围之内。

 

 

交叉验证

当样本数据比较小的时候，为了避免验证集“浪费”太多的训练数据，采用样本交叉验证的方法，并把平均值作为结果

 过拟合，欠拟合，正确拟合

 

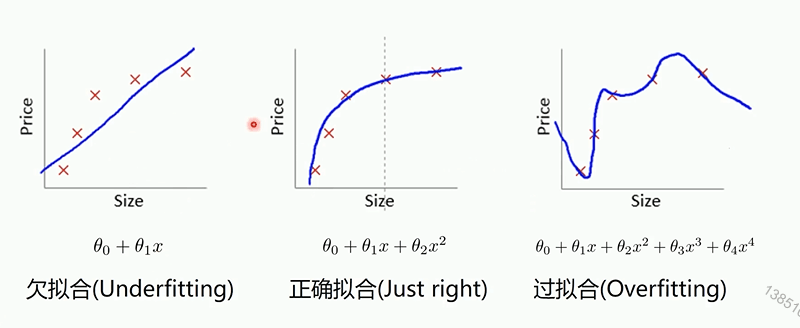
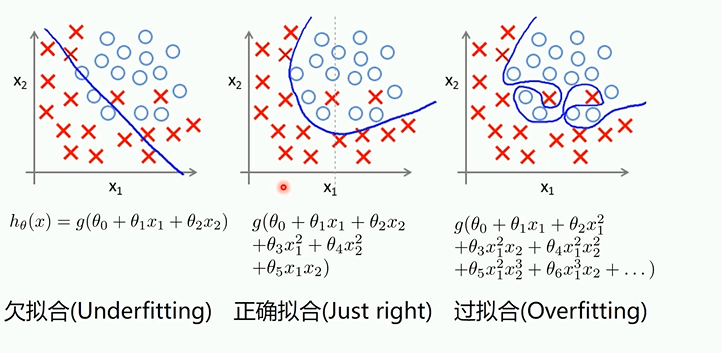
过拟合会导致训练集拟合效果好，测试集效果差，欠拟合都差。为防止过拟合 

正则化就是在原来的损失函数基础上加入一项，来减少高次项的值,使得曲线平滑

 

岭回归

 为解决标准方程法中存在的矩阵不可逆问题，引入了岭回归

 

 

import  numpy as np
from matplotlib import pyplot as plt
from sklearn import linear_model
#读取数据
data = np.genfromtxt("longley.csv", delimiter=',')
print(data)
#切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
#创建模型
#生成0.001到1的五十个岭系数值
alphas_to_test = np.linspace(0.001, 1)#从0.001到1共五十个数据，默认在start和end之间有50个数据，这五十个数据是假设的岭系数
model = linear_model.RidgeCV(alphas= alphas_to_test, store_cv_values= True)#store_cv_values表示存储每个岭系数和样本对应下的损失值
model.fit(x_data, y_data)
print(model.alpha_)#最小损失函数对应的岭系数
print(model.cv_values_.shape)#16*50的矩阵
#绘图
#岭系数和loss值得关系
plt.plot(alphas_to_test, model.cv_values_.mean(axis = 0))# 求在每个系数下对应的平均损失函数，axis=1表示横轴，方向从左到右；0表示纵轴，方向从上到下
plt.plot(model.alpha_, min(model.cv_values_.mean(axis = 0)),'ro')#最优点
plt.show()
model.predict(x_data[2,np.newaxis])#对一个样本进行预测

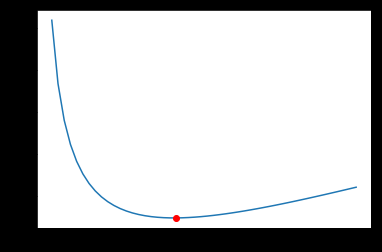岭系数和损失函数对应的关系图

 简单说一下arange,range,linspace的区别，arange和range都是在start和end之间以step作为等差数列对应的数组，只不过arange的step

可以是小数，而range必须为整数，而且arange属于numpy，linspace则是在start和end之间取num个数 np.linspace(start,end,num)

LASSO算法

由于岭回归计算得到的系数很难为0，而Lasso算法可以使一些指标为0  

 

 

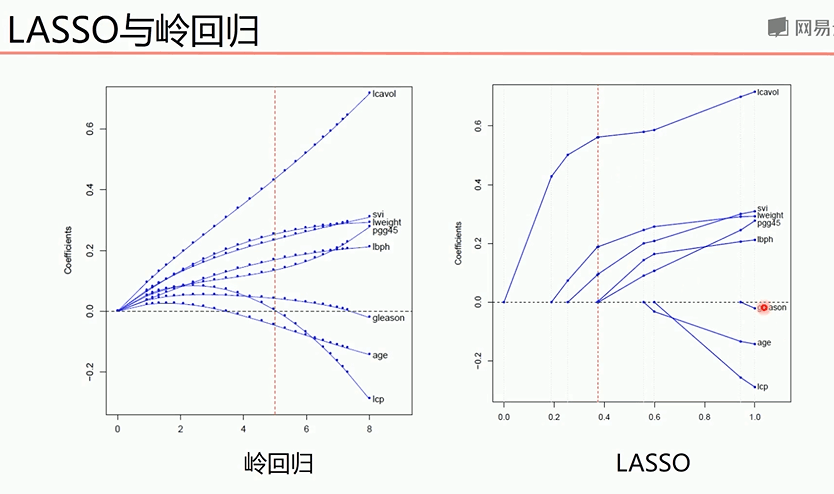
 从上图可以看出，LASSo在入系数某个取值下某些特征的系数就归为0了

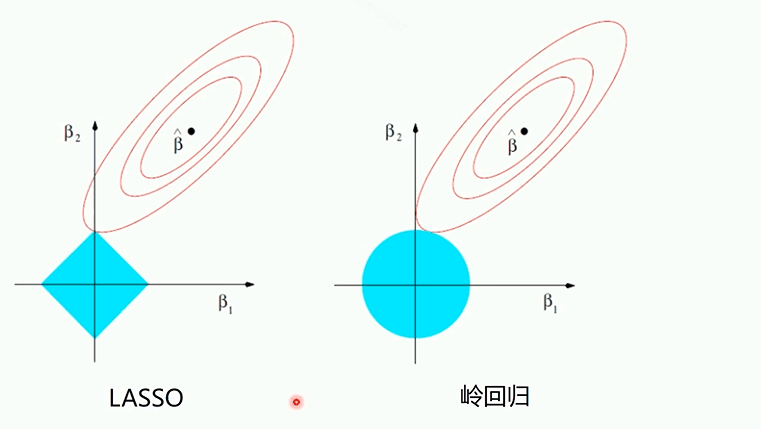
 交点处变为最优取值处

import  numpy as np
from matplotlib import pyplot as plt
from sklearn import linear_model
#读取数据
data = np.genfromtxt("longley.csv", delimiter=',')
print(data)
#切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
#创建模型
model = linear_model.LassoCV()
model.fit(x_data,y_data)
#lasso系数
print(model.alpha_)
#相关系数，发现某些系数为零，说明这些系数权重比较小，可以忽视
print(model.coef_)#[0.10206856 0.00409161 0.00354815 0.         0.         0.        ]
#验证
model.predict(x_data[-2,np.newaxis])

弹性网

 对lasso和岭系数方法综合起来

import  numpy as np
from matplotlib import pyplot as plt
from sklearn import linear_model
#读取数据
data = np.genfromtxt("longley.csv", delimiter=',')
print(data)
#切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
#创建模型
model = linear_model.ElasticNetCV()
model.fit(x_data,y_data)
#lasso系数
print(model.alpha_)
#相关系数，发现某些系数为零，说明这些系数权重比较小，可以忽视
print(model.coef_)#[0.10206856 0.00409161 0.00354815 0.         0.         0.        ]
#验证
print(model.predict(x_data[-2,np.newaxis]))

无偏估计和有偏估计