15.1问题的动机
将正常的样本绘制成图表（假设可以），如下图所示：
当新的测试样本同样绘制到图标上，如果偏离中心越远说明越可能不正常，使用某个可能性阈值，当低于正常可能性阈值时判断其为异常，然后做进一步的检查。异常检测常用于工业生产、异常用户等实际场景中。
以上这种方法叫密度评估：
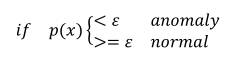
15.2高斯分布
（1）高斯分布也称为正态分布，其记为：
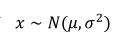
（2）高斯分布的概率密度函数：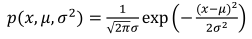
其中均值和方差的计算公式：
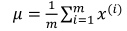
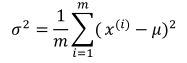
均值影响水平移动；方差越大，分布越矮胖，方差越小，分布越瘦高。
（3）在求均值方差是到底用1/m还是1/(m-1)不做深究，二者差别很小（除非数据样本特别少），机器学习上习惯用前者。
15.3算法
（1）首先求出每个特征的均值和方差：
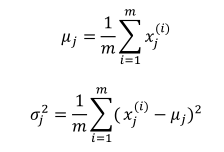
（2）获取新数据之后根据模型计算密度（注意此处算的是密度，而不是概率）：
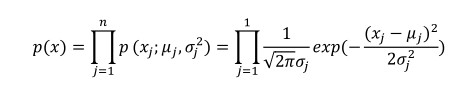（最后一项应该把1改成n）
（3）根据设定的判断边界，当p(x)小于判断边界是则判别为异常。
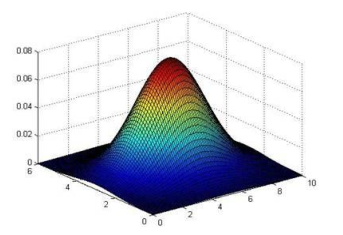
以下的三维图是表示密度估计函数：
15.4开发和评价一个异常检测系统
（1）异常检测是一个非监督学习，故不可以根据结果变量y的值来高斯我们数据是否真的是异常。
（2）异常检测系统开发的方法：从带有标记（正常和异常）的数据着手，选择部分正确数据集构建模型，然后剩余正常和异常构成交叉验证集和测试集，交叉验证集作为选取阈值ε
案例：10000台正常的引擎数据，20台异常引擎数据，分配如下：
6000台正常作为模型构建
2000台正常和10台异常作为交叉验证集
2000台正常和10台异常作为测试集
具体评价方法如下：
1.根据训练集数据，我们估计特征的平均值和方差并构建p(x)函数；
2.对交叉验证集，尝试用不同的ε值作为阈值，并预测数据是否异常，根据F1值或者查准率与查全率的比例来选择ε；
3.选出ε后，针对测试集进行预测，计算异常检测系统的F1值，或者计算出出查准率查全率之比。
15.5异常检测与监督学习的对比
通常来说，正例（异常）样本太少，甚至为0，也就是说，出现了太多没见过的不同的异常类型，对于这些问题，通常应该使用的算法是异常检测算法。
15.6选择特征
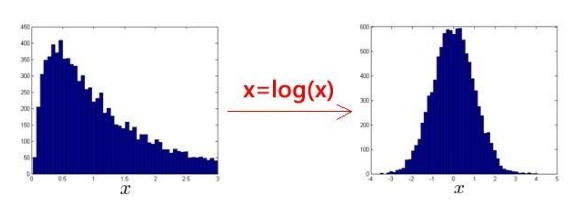
（1）异常检测是假设特征符合正态分布（不是当然也能用，但不好），故需要将非正态分布的特征转换成正态分布，例如使用对数函数x=log(x+C),其中C是非负常数，常用1；或者x=xc,c为0-1之间的一个分数。下图就是一个通过对数转换得到的正态分布
（2）误差分析：一个常见问题是一些异常的数据可能也会有较高的p(x)值，因而被认为是正常的，这种情况下可以做误差分析，从中找到一些新特征，是异常的p(x)变小。如下图中一个异常样本在一个特征中p(x)值很大，然后寻找其他特征，使其p(x)变小。
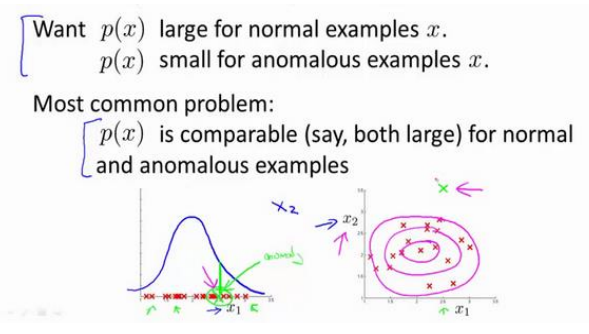
通常可以通过一些相关特征的组合获得很好的新特征，如在检测数据中心的计算机状况，使用CPU的负载与网络通信的比例作为新的特征，该值异常大时意味着出现问题。
15.7多元高斯分布（选修）
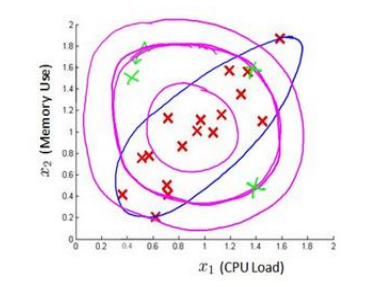
（1）当特征之间具有相关性时，原来的高斯分布可能无法正确的边界（当然通过特征组合成新特征可以一定的解决该问题），如下图紫色的线是原来的高斯分布，蓝色的线是多元高斯分布：
（2）原来的高斯分布计算过程：
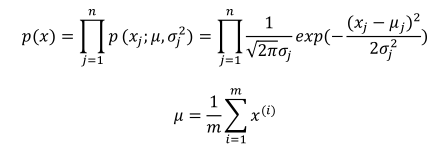
多元高斯分布计算过程（计算均值、协方差、概率密度函数）：
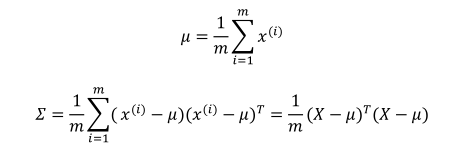
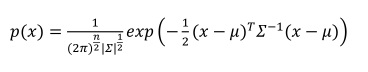
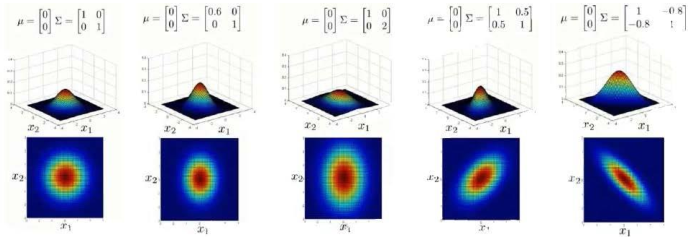
（3）协方差矩阵的影响：
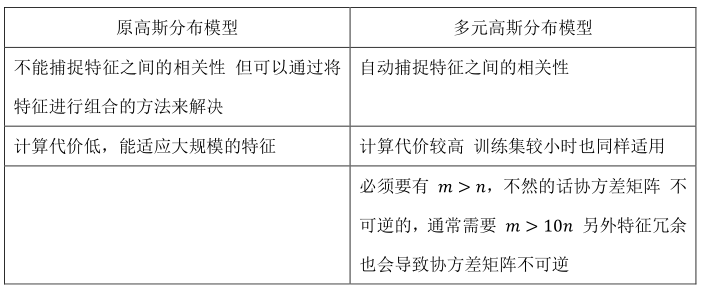
（4）原高斯分布模型（特例）与多元高斯分布模型（一般）的比较：
（5）特征之间具有相关性时，解决方法有二，其一通过 多元高斯分布，其二通过特征组合形成新特征。
15.8使用多元高斯分布进行异常检测（选修）：
简要的讲就是先用数据集计算均值和协方差，然后计算p(x),利用测试数据带入到p(x)中求得的值与阈值作比较，小于阈值则判断为异常。
