吴恩达《机器学习》课程总结(14)_降维

Q1动机一：数据压缩

将特征进行降维，如将相关的二维降到一维：

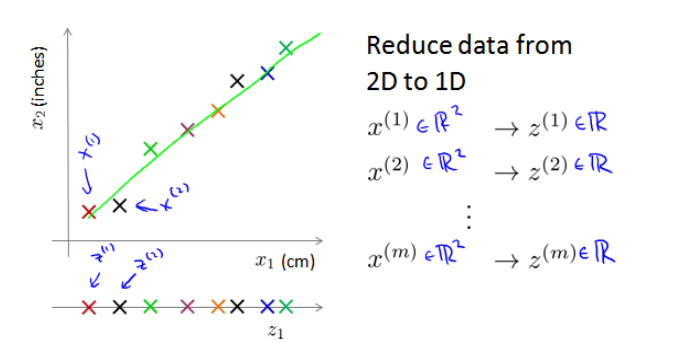
三维变二维：

以此类推把1000维数据降成100维数据。减少内存占用的空间

Q2动机二：数据可视化

如50个维度的数据是无法进行可视化的，使用降维的方法可以使其降到2维，然后进行可视化。

降维的算法只负责减少维度，新产生的特征的意义就必须有我们自己去发现了。

Q3主成分分析问题

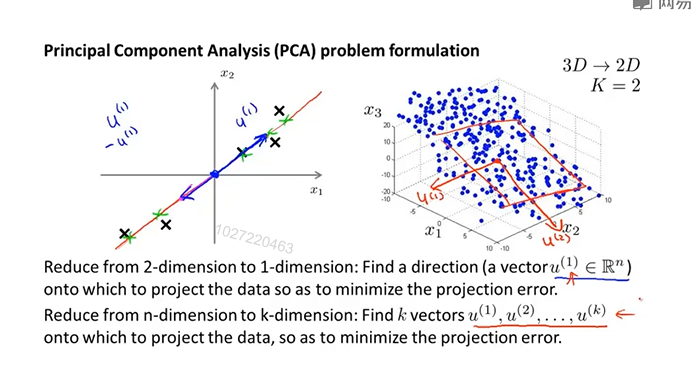
（1）主成分分析的问题描述：
问题是要将n维数据降至k维，目标是找到k个向量，使得总的投射误差最小。

（2）主成分分析与线性回归的比较：

二者是不同的算法，前者是最小化投影误差，后者是最小化预测误差；前者不做任何分析，后者目的是预测结果。

线性回归是垂直于轴投影，主成分分析是垂直于红线的投影。如下图所示：

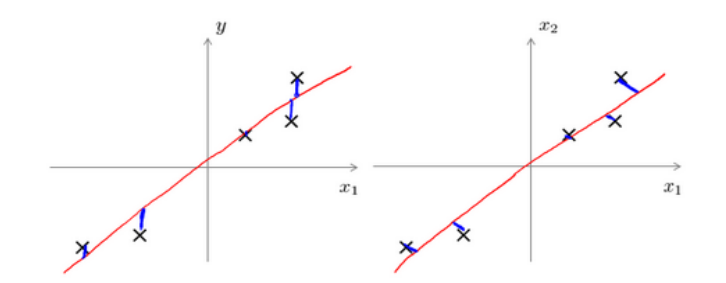
（3）PCA是对新求出来的“主元”向量的重要性进行排序，根据需要去前面重要的部分，将后面的维数省略。

（4）PCA的一个优点是完全依赖数据，而不需要人为设定参数，与用户是独立的；同时这也是也可以看做缺点，因为，如果用户对数据有一定的先验知识，将无法派上用场，可能得不到想要的效果。

Q4主成分分析算法

PCA将n维减少到k维：

（1）均值归一化，即减均值除以方差；

（2）计算协方差矩阵；

（3）计算协方差矩阵的特征向量；

对于一个n x n维度的矩阵，上式中的U是一个具有与数据之间最小投影误差的方向向量构成的矩阵，只需要去前面的k个向量获得n x k维度的向量，用U_reduce表示，然后通过如下计算获得要求的新的特征向量z^（i）=U^T_reduce*x^（i）。

Q5选择主成分的数量

主成分分析是减少投射的平均均方误差，训练集的方差为：

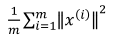
希望可以尽可能的减少二者的比值，比如希望二者的比值小于1%，选择满足这个条件的最小维度。

Q6重建的压缩表示

降维式子：

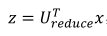
重建（即从低维回到高维）：

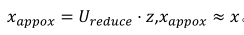
示意图如下所示：左图是降维，右图是重建。

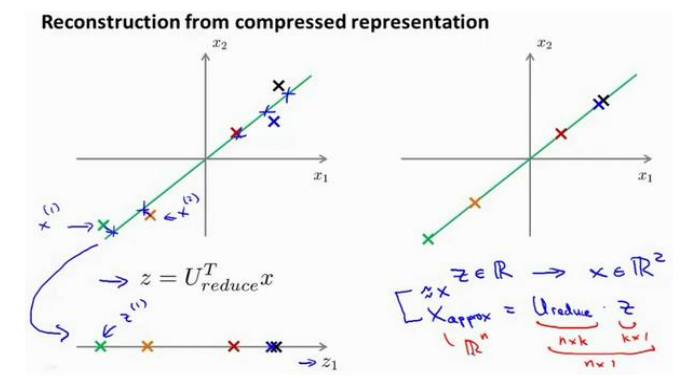
Q7主成分分析法的应用建议

正确使用案例：

100 x 100像素的图片，即10000维特征，采用PCA将其压缩至1000维，然后对训练集运行学习算法，在预测时，对测试集采用之前学到的U_reduce将测试集的x转换成z,再进行预测。

错误使用情况：

（1）尝试用PCA来解决过拟合，PCA是无法解决过拟合的，应该用正则化来解决。

（2）默认把PCA作为学习过程的一部分，其实应该尽量使用原始特征，只有在算法运行太慢或者占用内存太多的情况下才考虑使用主成分分析法。