一、实验目的:熟悉变换编码的图像压缩方法
二、实验内容:以所给图像为例,采用dct进行图像压缩编码,通过改变模板矩阵中非零元素的个数,得到不同缩编码图像, 根据公式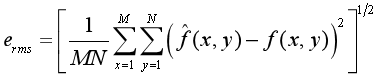
,编写程序计算原图像和dct变换后得到的图像之间的均方误差。用到的matlab函数为im2double,dctmtx,blkproc。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
先上实验要用到的图片
下面的程序的模板矩阵是8*8的
1 I=imread('C:/woman_blonde.tif'); 2 I=im2double(I); 3 T=dctmtx(8);%得到一个8*8的离散余弦变化矩阵 4 B=blkproc(I,[8 8],'P1*x*P2',T,T');% x就是每一个分成的8*8大小的块,P1*x*P2相当于像素块的处理函数,p1=T p2=T’,也就是fun=p1*x*p2'=T*x*T'的功能是进行离散余弦变换 5 m=[1 1 1 0 0 0 0 0 6 1 1 0 0 0 0 0 0 7 1 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 9 0 0 0 0 0 0 0 0 10 0 0 0 0 0 0 0 0 11 0 0 0 0 0 0 0 0 12 0 0 0 0 0 0 0 0 ]; 13 B2=blkproc(B,[8 8],'P1.*x',m);%舍弃每个块中的高频系数,达到图像压缩的目的 14 I2=blkproc(B2,[8 8],'P1*x*P2',T',T);%进行反余弦变换,得到压缩后的图象 15 cha=abs(I-I2); 16 junfang=mse(cha); 17 figure,imshow(I),title('原始图像','Fontsize',18); 18 figure,imshow(I2),title('压缩(解压缩)图像','Fontsize',18), 19 xlabel({'均方误差: ';junfang},'Fontsize',18);
下面的程序的模板矩阵是16*16的
1 I3=imread('C:/woman_blonde.tif'); 2 I3=im2double(I3); 3 T2=dctmtx(16); 4 B3=blkproc(I3,[16 16],'P1*x*P2',T2,T2'); 5 m2=[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 6 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 7 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 8 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 12 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 13 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 15 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 17 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 19 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 20 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]; 21 B4=blkproc(B3,[16 16],'P1.*x',m2); 22 I4=blkproc(B4,[16 16],'P1*x*P2',T2',T2); 23 cha1=abs(I3-I4); 24 junfang2=mse(cha1); 25 figure,imshow(I3),title('原始图像','Fontsize',20); 26 figure,imshow(I4),title('压缩(解压缩)图像','Fontsize',20), 27 xlabel({'均方误差: ';junfang2},'Fontsize',20);
对比运行结果:
8*8
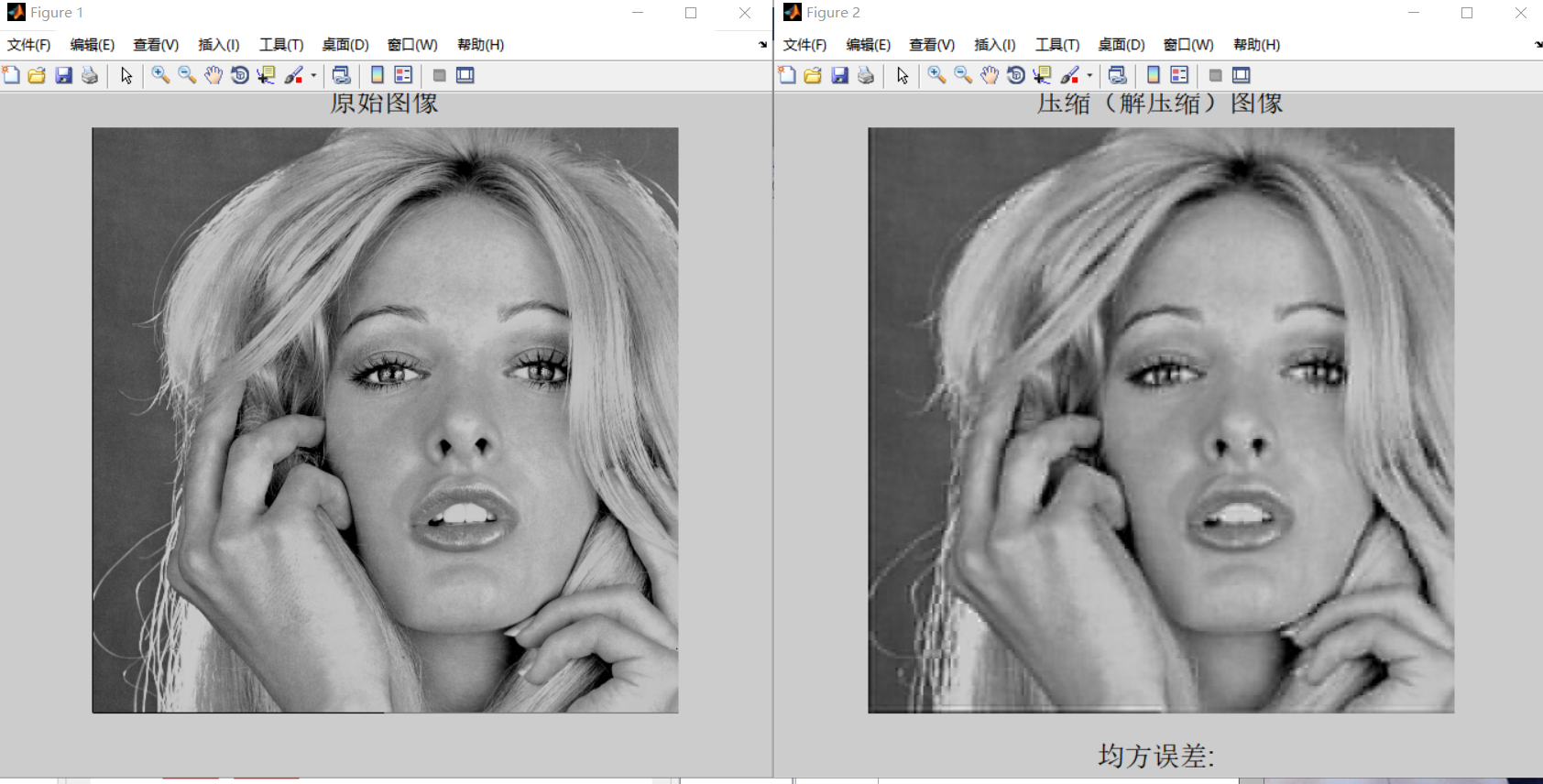
16*16
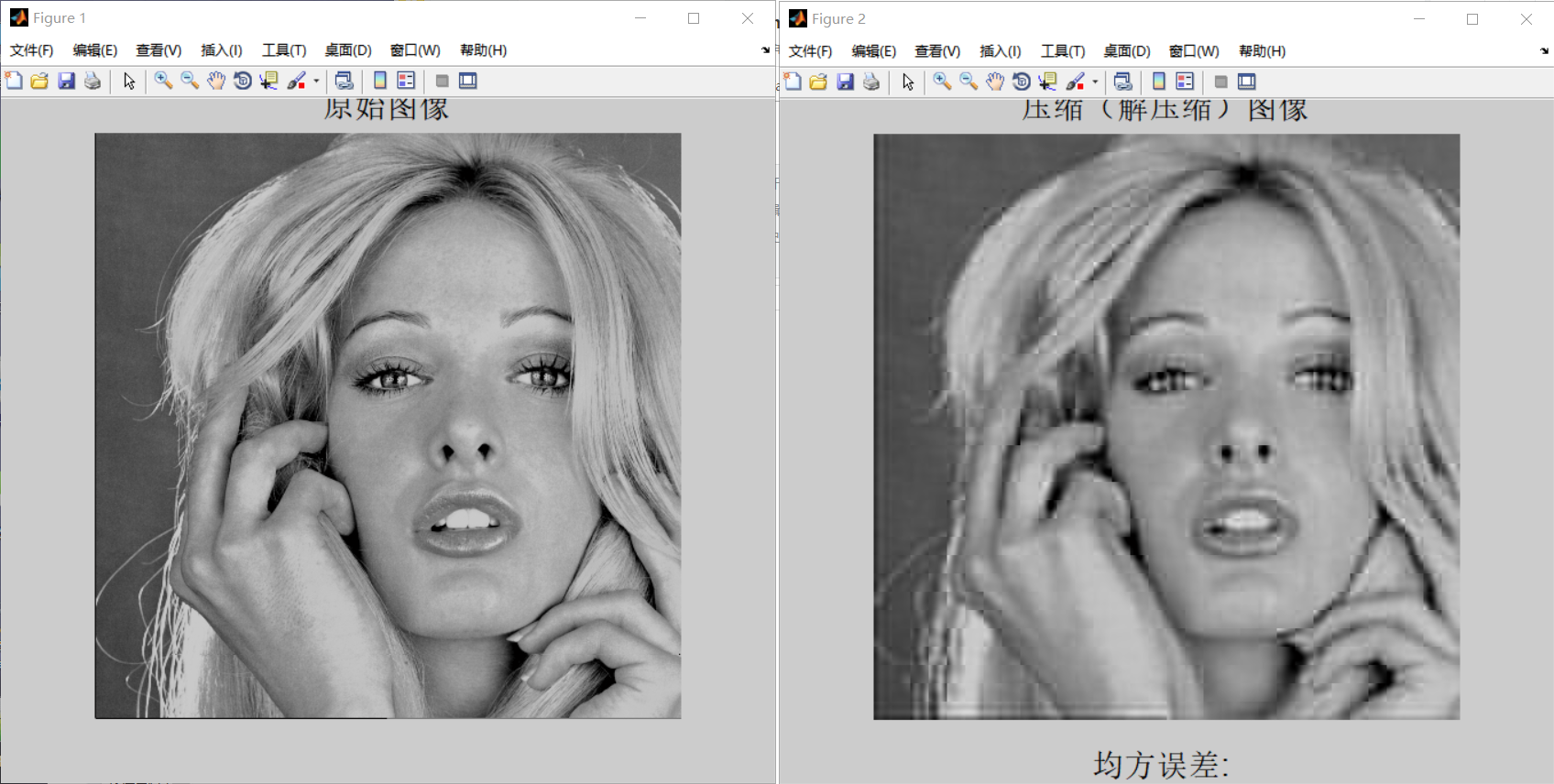
对比还是容易发现,第二个代码的运行结果图片损失程度还是比较大的,因程序二模板的0个数占比更多,使更多的高频像素被压缩,而该压缩是不可逆的,所以图二损失程度更大。
下面是程序中几个函数的说明
dctmtx
MATLAB图像处理工具箱实现离散余弦变换有两种方法:dct2和dctmtx(1)使用函数dct2,该函数用一个基于FFT的算法来提高当输入较大的方阵时的计算速度。 (2)使用由dctmtx函数返回的DCT变换矩阵,这种方法较适合于较小的输入方阵(例如8×8或16×16)。 ①函数:dct2 实现图像的二维离散余弦变换。调用格式为: B = dct2(A) B = dct2(A,[M N]) B = dct2(A,M,N) 式中A表示要变换的图像,M和N是可选参数,表示填充后的图像矩阵大小,B表示变换后得到的图像矩阵。 ②函数:dctmtx D = dctmtx(N) 式中D是返回N×N的DCT变换矩阵,如果矩阵A是N×N方阵,则A的DCT变换可用D×A×D’来计算。这在有时比dct2计算快,特别是对于A很大的情况。
blkproc
功能:对图像进行分块处理 函数调用形式:B = blkproc(A,[m n],fun, parameter1, parameter2, ...) B = blkproc(A,[m n],[mborder nborder],fun,...) B = blkproc(A,'indexed',...) 参数解释:[m n] :图像以m*n为分块单位,对图像进行处理(如8像素*8像素) Fun: 应用此函数对分别对每个m*n分块的像素进行处理 parameter1, parameter2: 要传给fun函数的参数 mborder nborder:对每个m*n块上下进行mborder个单位的扩充,左右进行nborder个单位的扩充,扩充的像素值为0,fun函数对整个扩充后的分块进行处理。
mse
等价于sum(a.^2)/lenght(a); MSE和RMSE都是网络的性能函数。MSE是(神经)网络的均方误差,叫"Mean Square Error"。比如有n对输入输出数据,每对为[Pi,Ti],i=1,2,...,n.网络通过训练后有网络输出,记为Yi。那MSE=(求和(Ti-Yi)^2(i=1,2,..n))/n,即每一组数的误差平方和再除以数据的对数。RMSE叫“Root Mean Square Error”,即在MSE基础上要开根号,中文译为“均方根误差”,MSE=MSE开根号。亦即RMSE是MSE的平方根。
