「NOI2016」优秀的拆分
题目描述
如果一个字符串可以被拆分为 ( ext{AABB}) 的形式,其中 ( ext{A}) 和 ( ext{B}) 是任意非空字符串,则我们称该字符串的这种拆分是优秀的。
例如,对于字符串 ( ext {aabaabaa}) ,如果令 ( ext{A}= exttt{aab}),( ext{B}= exttt{a}),我们就找到了这个字符串拆分成 ( ext{AABB}) 的一种方式。
一个字符串可能没有优秀的拆分,也可能存在不止一种优秀的拆分。
比如我们令 ( ext{A}= exttt{a}),( ext{B}= exttt{baa}),也可以用 ( ext{AABB}) 表示出上述字符串;但是,字符串 ( exttt{abaabaa}) 就没有优秀的拆分。
现在给出一个长度为 (n) 的字符串 (S),我们需要求出,在它所有子串的所有拆分方式中,优秀拆分的总个数。这里的子串是指字符串中连续的一段。
以下事项需要注意:
- 出现在不同位置的相同子串,我们认为是不同的子串,它们的优秀拆分均会被记入答案。
- 在一个拆分中,允许出现 ( ext{A}= ext{B})。例如 ( exttt{cccc}) 存在拆分 ( ext{A}= ext{B}= exttt{c})。
- 字符串本身也是它的一个子串。
输入格式
每个输入文件包含多组数据。
输入文件的第一行只有一个整数 (T),表示数据的组数。
接下来 (T) 行,每行包含一个仅由英文小写字母构成的字符串 (S),意义如题所述。
输出格式
输出 (T) 行,每行包含一个整数,表示字符串 (S) 所有子串的所有拆分中,总共有多少个是优秀的拆分。
样例
样例输入
4
aabbbb
cccccc
aabaabaabaa
bbaabaababaaba
样例输出
3
5
4
7
样例解释
我们用 (S[i, j]) 表示字符串 (S) 第 (i) 个字符到第 (j) 个字符的子串(从 (1) 开始计数)。
第一组数据中,共有三个子串存在优秀的拆分:
(S[1,4]= ext{aabb}),优秀的拆分为 ( ext{A}= exttt{a}),( ext{B}= exttt{b});
(S[3,6]= ext{bbbb}),优秀的拆分为 ( ext{A}= exttt{b}),( ext{B}= exttt{b});
(S[1,6]= ext{aabbbb}),优秀的拆分为 ( ext{A}= exttt{a}),( ext{B}= exttt{bb})。
而剩下的子串不存在优秀的拆分,所以第一组数据的答案是 (3)。
第二组数据中,有两类,总共四个子串存在优秀的拆分:
对于子串 (S[1,4]=S[2,5]=S[3,6]= ext{cccc}),它们优秀的拆分相同,均为 ( ext{A}= exttt{c}),( ext{B}= exttt{c}),但由于这些子串位置不同,因此要计算三次;
对于子串 (S[1,6]= ext{cccccc}),它优秀的拆分有两种:( ext{A}= exttt{c}),( ext{B}= exttt{cc}) 和 ( ext{A}= exttt{cc}),( ext{B}= exttt{c}),它们是相同子串的不同拆分,也都要计入答案。
所以第二组数据的答案是 (3+2=5)。
第三组数据中,(S[1,8]) 和 (S[4,11]) 各有两种优秀的拆分,其中 (S[1,8]) 是问题描述中的例子,所以答案是 (2+2=4)。
第四组数据中,(S[1,4]),(S[6,11]),(S[7,12]),(S[2,11]),(S[1,8]) 各有一种优秀的拆分,(S[3,14]) 有两种优秀的拆分,所以答案是 (5+2=7)。
数据范围与提示
对于全部的测试点,(1 leq T leq 10, n leq 30000)。
题解
(95)分hash暴力真的就是随便写...
我们处理出(a[i])和(b[i])表示以(i)为终点和起点的(AA)串的个数。那么答案即为(sum_{i=1}^{n-1}a[i] imes b[i + 1])。hash优化一下判定过程就是(O(n^2))的。
(100)分不看题解真的没有什么思路(即使知道了这是一道后缀数组题...)
我们可以思考一下如何优化处理(AA)串的过程。
枚举(A)串的长度(len),然后对于相邻的两个长度间隔为(len)的点,如果他们的(lcp(x,y)+lcs(x,y)geq len),那么中间则有一段长度为(lcp+lcs-len+1)的合法的(AA)串终点的区间。
为什么呢?可以通过把这句话画出来,比如这样:
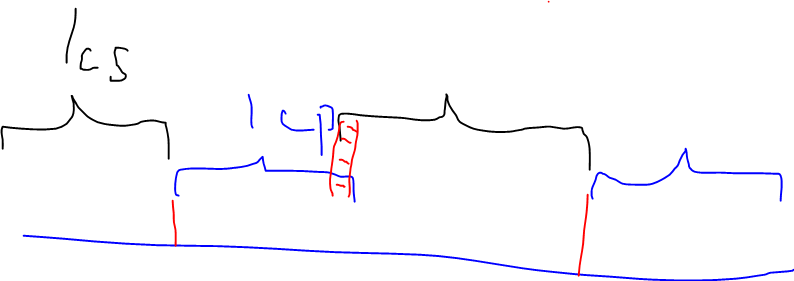
那么中间那段红色的区域就是合法的终点区间。
(lcp(x,y))和(lcs(x,y))可以直接用后缀数组来求。总复杂度为(O(n log n))。
当然也可以用hash实现这个过程,复杂度就是(O(n log^2 n))的。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 50010;
int n, a[N], b[N];
char s[N];
struct SA {
int sa[N], height[N], tong[N], rnk[N], tp[N], f[N][16], LG[N];
int m;
void radix_sort() {
for(int i = 1; i <= m; ++i) tong[i] = 0;
for(int i = 1; i <= n; ++i) tong[rnk[i]]++;
for(int i = 1; i <= m; ++i) tong[i] += tong[i - 1];
for(int i = n; i; --i) sa[tong[rnk[tp[i]]]--] = tp[i];
}
int query(int l, int r) {
l = rnk[l], r = rnk[r];
if(l > r) swap(l, r); ++l;
int k = LG[r - l + 1];
return min(f[l][k], f[r - (1 << k) + 1][k]);
}
void init() {
memset(sa, 0, sizeof(sa));
memset(height, 0, sizeof(height));
memset(tong, 0, sizeof(tong));
memset(rnk, 0, sizeof(rnk));
memset(tp, 0, sizeof(tp));
memset(f, 0, sizeof(f));
memset(LG, 0, sizeof(LG));
}
void build(char *A) {
init();
for(int i = 1; i <= n; ++i) rnk[i] = A[i], tp[i] = i;
m = 200; radix_sort();
for(int w = 1, p = 0; w <= n && p < n; m = p, w <<= 1) {
p = 0;
for(int i = 1; i <= w; ++i) tp[++p] = n - w + i;
for(int i = 1; i <= n; ++i) if(sa[i] > w) tp[++p] = sa[i] - w;
radix_sort(); swap(tp, rnk); rnk[sa[1]] = p = 1;
for(int i = 2; i <= n; ++i)
rnk[sa[i]] = (tp[sa[i]] == tp[sa[i - 1]] && tp[sa[i] + w] == tp[sa[i - 1] + w]) ? p : ++p;
}
for(int i = 1, k = 0; i <= n; ++i) {
if(k) --k; int j = sa[rnk[i] - 1];
while(A[i + k] == A[j + k] && i + k <= n && j + k <= n) ++k;
height[rnk[i]] = k;
}
for(int i = 2; i <= n; ++i) LG[i] = LG[i >> 1] + 1;
for(int i = 1; i <= n; ++i) f[i][0] = height[i];
for(int j = 1; j <= 15; ++j)
for(int i = 1; i + (1 << j) - 1 <= n; ++i) {
f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}
}
}A, B;
int main() {
int T = 0; scanf("%d", &T); while(T--) {
memset(a, 0, sizeof(a));
memset(b, 0, sizeof(b));
scanf("%s", s + 1); n = strlen(s + 1);
A.build(s); reverse(s + 1, s + n + 1); B.build(s);
for(int len = 1; len <= (n >> 1); ++len) {
for(int i = len, j = i + len; j <= n; i += len, j += len) {
int LCS = min(len - 1, B.query(n - i + 2, n - j + 2)), LCP = min(len, A.query(i, j));
if(LCS + LCP >= len) {
int t = LCP + LCS - len + 1;
a[i - LCS]++; a[i - LCS + t]--;
b[j + LCP - t]++; b[j + LCP]--;
}
}
}
for(int i = 1; i <= n; ++i) a[i] += a[i - 1], b[i] += b[i - 1];
ll ans = 0;
for(int i = 1; i < n; ++i) ans += 1LL * b[i] * a[i + 1];
printf("%lld
", ans);
}
return 0;
}