题目地址
这题各大OJ都有,放几个我交过的OJ里面这题的链接,下面的题面copy自BZOJ
Luogu
LOJ
BZOJ
Description
小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。天天爱跑步是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一一棵包含 N个结点和N-1 条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从1到N的连续正整数。
现在有个玩家,第个玩家的起点为Si ,终点为Ti 。每天打卡任务开始时,所有玩家在第0秒同时从自己的起点出发, 以每秒跑一条边的速度,不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)
小C想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点的观察员会选择在第Wj秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第Wj秒也理到达了结点J 。 小C想知道每个观察员会观察到多少人
注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点J作为终点的玩家: 若他在第Wj秒重到达终点,则在结点J的观察员不能观察到该玩家;若他正好在第Wj秒到达终点,则在结点的观察员可以观察到这个玩家。
Input
第一行有两个整数N和M 。其中N代表树的结点数量, 同时也是观察员的数量, M代表玩家的数量。
接下来n-1 行每行两个整数U和V ,表示结点U 到结点V 有一条边。
接下来一行N 个整数,其中第个整数为Wj , 表示结点出现观察员的时间。
接下来 M行,每行两个整数Si和Ti,表示一个玩家的起点和终点。
对于所有的数据,保证 1<=Si,Ti<=N,0<=Wj<=N
Output
输出1行N 个整数,第个整数表示结点的观察员可以观察到多少人。
Sample Input
6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6
Sample Output
2 0 0 1 1 1
HINT
对于1号点,W1=0,故只有起点为1号点的玩家才会被观察到,所以玩家1和玩家2被观察到,共2人被观察到。
对于2号点,没有玩家在第2秒时在此结点,共0人被观察到。
对于3号点,没有玩家在第5秒时在此结点,共0人被观察到。
对于4号点,玩家1被观察到,共1人被观察到。
对于5号点,玩家1被观察到,共1人被观察到。
对于6号点,玩家3被观察到,共1人被观察到
Solution
NOIP2016最难的一道题,这题花了我一天时间qwq,代码写了9kb(我每个部分分都写了)
网上关于正解的题解很多,所以这里主要是介绍一下部分分做法,所有部分分做法都有讲到
首先先看一下都有哪些部分分,各档部分分加起来足有80分,还是挺良心的qwq
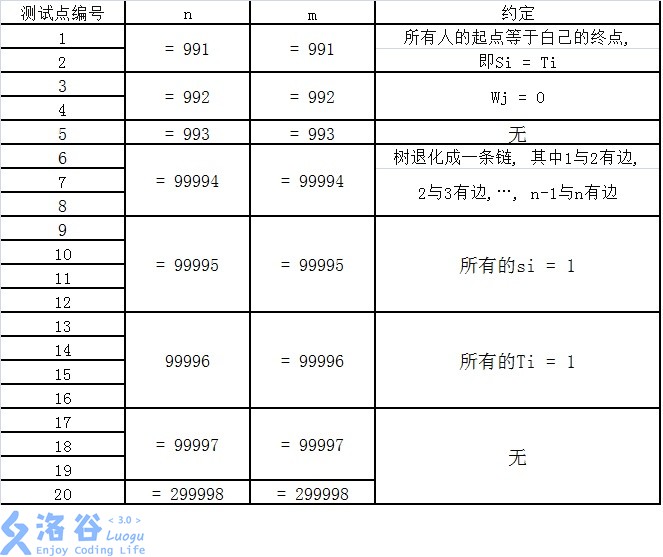
这篇题解在讲述时不会按照测试点顺序来讲,而是由易到难地讲解部分分做法,最后讲正解
出于行文需要,做出以下规定:
每个人走的路径下文直接称路径
对于每个部分点,读入部分省去,只保留关键代码,文末有完整代码(下同)
1. 测试点1,2(10分)
这两个点保证每条路径的(S_i=T_i)
很容易想到的就是只有这个点的(w_i=0)才能观察到这条路径。
于是对于每条路径,判一下(w_i)是否为0,如果为0,则该点的答案+1
void solve1() {
for(int i = 1; i <= m; i ++) {
int s = read(), t = read();
if(w[s] == 0) ans[s] ++;
}
for(int i = 1; i <= n; i ++) out(ans[i]), putchar(' ');
}
2.测试点3,4(10分)
这两个点保证所有点的(w)值为0,所以只有起点能观察到这条路径
对每条路径的起点的答案+1即可
void solve2() {
for(int i = 1; i <= m; i ++) {
int s = read(), t = read();
ans[s] ++;
}
for(int i = 1; i <= n; i ++) out(ans[i]), putchar(' ');
}
3.测试点5(5分)
这个点没有什么性质,但是(n,m<=1000)
所以直接暴力跑lca判断即可
void dfs1(int u) {
siz[u] = 1;
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
fa[e[i].to] = u;
dep[e[i].to] = dep[u] + 1;
dfs1(e[i].to);
siz[u] += siz[e[i].to];
}
}
int tim;
void dfs2(int u, int topf) {
top[u] = topf;
id[u] = ++ tim;
int k = 0;
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
if(siz[e[i].to] > siz[k]) k = e[i].to;
}
if(!k) return;
dfs2(k, topf);
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u] || e[i].to == k) continue;
dfs2(e[i].to, e[i].to);
}
}
int lca(int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
return x;
}
void solve() {
dfs1(1);dfs2(1,1);
for(int i = 1; i <= m; i ++) {
int s = read(), t = read();
int l = lca(s, t), tot = 0;
for(int k = s; k != l; k = fa[k]) {
if(w[k] == tot) ans[k] ++;
++tot;
}
if(w[l] == tot) ans[l] ++;
tot += dep[t] - dep[l];
for(int k = t; k != l; k = fa[k]) {
if(w[k] == tot) ans[k] ++;
--tot;
}
}
for(int i = 1; i <= n; i ++) out(ans[i]), putchar(' ');
}
4.测试点9,10,11,12(20分)
这几个测试点保证(S_i=0)
这个性质有什么作用呢,经过一番思索不难想到,每条路径上的点,当且仅当(dep_i=w_i)时,这个点能观察到这条路径
但是对于每条路径进行统计有点困难
这里有两种方法
1.树链剖分+线段树
将会给出这种做法的代码
实际上就是优化了一下暴力,给每条路径上的点都+1,利用树链剖分来实现
最后遍历一遍整棵树,就可以得到答案了(注意只有(w_i=dep_i)的点的答案才是有效的)
效率是(O(nlognlogn))
namespace tree_chain {
void dfs1(int u) {
siz[u] = 1;
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
fa[e[i].to] = u;
dep[e[i].to] = dep[u] + 1;
dfs1(e[i].to);
siz[u] += siz[e[i].to];
}
}
int tim;
void dfs2(int u, int topf) {
top[u] = topf;
id[u] = ++ tim;
int k = 0;
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
if(siz[e[i].to] > siz[k]) k = e[i].to;
}
if(!k) return;
dfs2(k, topf);
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u] || e[i].to == k) continue;
dfs2(e[i].to, e[i].to);
}
}
int lca(int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
return x;
}
struct tree {
int l, r, sum, add;
}t[N<<2];
#define mid ((l + r) >> 1)
#define lc (rt << 1)
#define rc (rt << 1 | 1)
void build(int l, int r, int rt) {
t[rt].l = l; t[rt].r = r;
if(l == r) return;
build(l, mid, lc); build(mid + 1, r, rc);
}
void pushup(int rt) {t[rt].sum = t[lc].sum + t[rc].sum;}
#define l t[rt].l
#define r t[rt].r
void pushdown(int ln, int rn, int rt) {
if(t[rt].add) {
int &x = t[rt].add;
t[lc].sum += x * ln; t[rc].sum += x * rn;
t[lc].add += x; t[rc].add += x;
x = 0;
}
}
void upd(int L, int R, int c, int rt) {
if(L <= l && r <= R) {
t[rt].sum += c * (r - l + 1);
t[rt].add += c;
return;
}
pushdown(mid - l + 1, r - mid, rt);
if(L <= mid) upd(L, R, c, lc);
if(R > mid) upd(L, R, c, rc);
pushup(rt);
}
int query(int L, int R, int rt) {
if(L <= l && r <= R) return t[rt].sum;
pushdown(mid - l + 1, r - mid, rt); int ans = 0;
if(L <= mid) ans += query(L, R, lc);
if(R > mid) ans += query(L, R, rc);
return ans;
}
#undef lc
#undef rc
#undef l
#undef r
#undef mid
void add(int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
upd(id[top[x]], id[x], 1, 1);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
upd(id[x], id[y], 1, 1);
}
}
using namespace tree_chain;
namespace pts_3 {
void solve() {
for(int i = 1; i <= m; i ++) {
int s = read(), t = read();
add(s, t);
}
for(int i = 1; i <= n; i ++) {
if(w[i] == dep[i]) {
ans[i] = query(id[i], id[i], 1);
}
}
for(int i = 1; i <= n; i ++) {
out(ans[i]), putchar(' ');
}
}
}
2.树上差分
这是一个我在思路逐步接近正解之后才明白的做法(其实每一档都在暗示正解)
我们可以把这个问题转化为贡献问题,我们把每条路径的起点+1,终点-1(在这里终点-1其实可以不用)
那么这个点在多少条路径里面也就直接查询子树和就可以了
这样我们就把这个问题转化为了查询子树贡献和的问题,所有点的子树贡献可以(O(n))遍历得到答案
总的复杂度为(O(n))
但是我没有写这种做法qwq
5.测试点13,14,15,16(20分)
这些测试点保证(T_i=1)。所有路径的终点都在1,考虑这个性质有啥用
对于一个路径上的点i,它能观察到这条路径的条件是(dep_S-dep_i=w_i)!
移项一下,就变成了(dep_S=w_i+dep_i)
考虑一下我们在上面说过的树上差分做法
事实上是差不多的,标记所有路径的起点,最后遍历一次子树,用桶储存每个深度各有几个起点
那么对于一个点,它的答案就是子树内(dep_S=w_i+dep_i)的(S)的数量(注意要在递归进子树时记录下桶内的值,回溯之后再记录一下,两值之差才是答案)
namespace pts_4 {
// t = 1
// dep[s]-dep[i]=w[i]则有贡献
// 即 dep[s]=w[i]+dep[i]
void dfs(int u) {
if(qwq[u]) total[dep[u]] += qwq[u];
int t = total[f[u]];
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
dfs(e[i].to);
}
ans[u] = total[f[u]] - t;
}
void solve() {
for(int i = 1; i <= n; i ++) f[i] = w[i] + dep[i];
for(int i = 1; i <= m; i ++) {
int s = read(), t = read();
qwq[s]++;
}
dfs(1);
for(int i = 1; i <= n; i ++) {
out(ans[i]), putchar(' ');
}
}
}
6.测试点6,7,8(15分)
这是一条链。
有什么用呢?在做完上面的(S_i=1)和(T_i=1)的部分分后,再思索一下大概就能想出来链的做法了。
我们可以把这条链放成横的,那么就变成了一段序列。
那么路径的方向显然就有从左到右,从右到左两种。
我们可以分类讨论一下,先说从左到右的。
因为路径每秒前进一个单位长度,所以不难想到的是对于一条路径上的点i,它能被观察到的话,一定满足(dep_i-dep_s=w_i)。
移项一下,(dep_i-w_i=dep_s)
是不是莫名熟悉!事实上和上面的两个部分分做法并没有什么本质区别!
但是链比上面两个部分分做法难的是,它的起点和终点都不是固定的
所以我们并不能像上面那样简单的去处理,但是思路可以继续沿用
起点+1,终点-1!树上差分!
我们考虑维护一个类似于桶的数组,设为(A[i]),它表示经过i点而且还没有结束的路径的条数,那么显然,每个点i的答案就是(A[dep_i+w_i])
如何维护这个数组?可以利用vector来实现对于路径的维护,这个可以参考一下正解的代码,我当时做这个部分点时并不是这么做的。
而从右到左的情况是完全类似的。式子变为(dep_i+w_i=dep_s)即可
另外一种方法:
从上面的分析,我们可以知道,对于一个点(i),只有两种路径会对它产生贡献
1.起点在(dep_i-w_i),且终点在(i)右边
2.起点在(dep_i+w_i),且终点在(i)左边
也就是说,终点其实只是一个判定条件!
那么我们可以用类似邻接表存图的方法,将起点和终点连边!
我们知道,邻接表的遍历
for(int i = head[u]; i; i = e[i].nxt)
就是遍历所有与它相连的边
所以我们这样连边然后遍历了一次之后也就可以找出所有起点在(head[u])的路径的终点了!一一判定即可
复杂度是(O(n))的(每条路径会被遍历一次,每个点会被遍历一次,n,m同阶,所以复杂度为(O(n)))
实际代码中使用vector模拟邻接表。
namespace pts_5 {
//链的情况
//要么s>t 要么s <= t
//考虑s <= t
//对于s -> t路径上的i,只有i - s = w[i]时才有贡献
//i-w[i]=s
//设f[i]=i-w[i]
//即s=f[i]时,才有贡献
//s > t同理
//所以对于一个点i,对它有贡献的点一定是起点为i-w[i]/i+w[i]且终点过i的路径的个数
vector<int> G[N];
void solve() {
for(int i = 1; i <= m; i ++) {
int S = read(), T = read();
G[S].push_back(T);
}
for(int i = 1; i <= n; i ++) {
int tot = 0;
if(i - w[i] > 0)
for(int j = 0, len = G[i - w[i]].size(); j < len; j ++) {
if(G[i - w[i]][j] >= i) tot ++;
}
if(i + w[i] <= n)
for(int j = 0, len = G[i + w[i]].size(); j < len; j ++) {
if(G[i + w[i]][j] <= i) tot ++;
}
ans[i] = tot;
}
for(int i = 1; i <= n; i ++) out(ans[i]), putchar(' ');
}
}
那么至此,我们已经讲完所有的部分分。部分分还是给的很足的。
可以发现,所有的部分分(除了暴力)都在把我们往一个方向带,也就是正解的方向!(赤裸裸的暗示)
虽然我写的时候跑歪了...是都写了,但是其中45分都是用奇奇怪怪的方法来拿的,对想正解没有啥帮助(树剖和模拟邻接表)
7.测试点17,18,19,20(20分)
就是正解了。
可以发现其实链的做法很接近正解了。各档部分分也在暗示着正解的做法。
在结合一下(S_i=1,T_i=1)的做法以及平时做到的关于树的题目的常见套路
可以猜出来的是,我们要拆路径!
拆成(S->LCA(S,T),LCA(S,T)->T)
这样每一部分其实就对应了链的做法了,处理的时候再套上(S_i=1和T_i=1)的做法,就可以了
具体做法大概是这样的:
我们先讨论(S->LCA(S,T))这条路径
首先对应链做法,我们可以得到式子(dep_s=dep_i-w_i)
那么我们再套上处理先前的树上差分做法(起点+1终点-1)
就可以处理了
至于(LCA(S,T)->T)这一段。
我们可以推出的式子是(dep_T-dep_i=len-w_i)
即(dep_T-len=dep_i-w_i)
(len为该条路径长度)
用类似的做法即可。
但是注意这样子等式两边都可能是负数,所以整体右移个(3*10^5)即可
复杂度是(O(nlogn))的(复杂度瓶颈在找LCA,所以其实可以用tarjan做到(O(n+m)))
具体处理上有一些要注意的就是
1.可以利用vector来处理(这样数组好开)
2.处理顺序要注意,要先给起点加上贡献,然后再算出这个点的答案,最后再减去终点的贡献
3.拆出来的链分开处理
代码(这个是完整的代码)
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define il inline
namespace io {
#define in(a) a=read()
#define out(a) write(a)
#define outn(a) out(a),putchar('
')
#define I_int int
inline I_int read() {
I_int x = 0, f = 1; char c = getchar();
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
char F[ 200 ] ;
inline void write( I_int x ) {
if( x == 0 ) { putchar( '0' ) ; return ; }
I_int tmp = x > 0 ? x : -x ;
if( x < 0 ) putchar( '-' ) ;
int cnt = 0 ;
while( tmp > 0 ) {
F[ cnt ++ ] = tmp % 10 + '0' ;
tmp /= 10 ;
}
while( cnt > 0 ) putchar( F[ -- cnt ] ) ;
}
#undef I_int
}
using namespace io ;
using namespace std ;
#define N 300010
int siz[N], dep[N], top[N], fa[N], id[N];
int n, m, f[N], qwq[N], total[N * 2], QAQ[N * 3];
int cnt, head[N], w[N];
int ans[N];
struct edge {
int to, nxt;
}e[N<<1];
void ins(int u, int v) {
e[++cnt] = (edge) {v, head[u]};
head[u] = cnt;
}
namespace tree_chain {
void dfs1(int u) {
siz[u] = 1;
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
fa[e[i].to] = u;
dep[e[i].to] = dep[u] + 1;
dfs1(e[i].to);
siz[u] += siz[e[i].to];
}
}
int tim;
void dfs2(int u, int topf) {
top[u] = topf;
id[u] = ++ tim;
int k = 0;
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
if(siz[e[i].to] > siz[k]) k = e[i].to;
}
if(!k) return;
dfs2(k, topf);
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u] || e[i].to == k) continue;
dfs2(e[i].to, e[i].to);
}
}
int lca(int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
return x;
}
struct tree {
int l, r, sum, add;
}t[N<<2];
#define mid ((l + r) >> 1)
#define lc (rt << 1)
#define rc (rt << 1 | 1)
void build(int l, int r, int rt) {
t[rt].l = l; t[rt].r = r;
if(l == r) return;
build(l, mid, lc); build(mid + 1, r, rc);
}
void pushup(int rt) {t[rt].sum = t[lc].sum + t[rc].sum;}
#define l t[rt].l
#define r t[rt].r
void pushdown(int ln, int rn, int rt) {
if(t[rt].add) {
int &x = t[rt].add;
t[lc].sum += x * ln; t[rc].sum += x * rn;
t[lc].add += x; t[rc].add += x;
x = 0;
}
}
void upd(int L, int R, int c, int rt) {
if(L <= l && r <= R) {
t[rt].sum += c * (r - l + 1);
t[rt].add += c;
return;
}
pushdown(mid - l + 1, r - mid, rt);
if(L <= mid) upd(L, R, c, lc);
if(R > mid) upd(L, R, c, rc);
pushup(rt);
}
int query(int L, int R, int rt) {
if(L <= l && r <= R) return t[rt].sum;
pushdown(mid - l + 1, r - mid, rt); int ans = 0;
if(L <= mid) ans += query(L, R, lc);
if(R > mid) ans += query(L, R, rc);
return ans;
}
#undef lc
#undef rc
#undef l
#undef r
#undef mid
}
using namespace tree_chain;
namespace pts_6 {
struct ques {
int s, t, l, len;
} q[N];
vector<int>v1[N*2], v2[N*2], v3[N * 2];
int Max_dep = 0;
//对于u->lca(u,v)
//同链做法
void dfs_1(int u) {
int now = w[u] + dep[u] + 300000, t = total[now];
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
dfs_1(e[i].to);
}
total[dep[u] + 300000] += qwq[u];
ans[u] += total[now] - t;
for(int i = 0, len = v3[u].size(); i < len; i ++) total[dep[v3[u][i]] + 300000] --;
}
//对于lca(u,v) -> v
//可得式子:
//dep[t]-dep[i] = len - w[i]
//移项得
//dep[t] - len = dep[i] - w[i]
void dfs_2(int u) {
int now = w[u] - dep[u] + 300000;
int t = QAQ[now];
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
dfs_2(e[i].to);
}
for(int i = 0, len = v2[u].size(); i < len; i ++) QAQ[300000 + v2[u][i]] ++;
ans[u] += QAQ[now] - t;
for(int i = 0, len = v1[u].size(); i < len; i ++) QAQ[300000 + v1[u][i]] --;
}
void solve() {
for(int i = 1; i <= n; i ++) Max_dep = max(Max_dep, dep[i]);
for(int i = 1; i <= m; i ++) {
int s = read(), t = read(), l = lca(s, t);
int len = dep[s] + dep[t] - 2 * dep[l];
q[i] = (ques) {s, t, l, len};
v3[l].push_back(s); qwq[s] ++;
}
dfs_1(1);
for(int i = 1; i <= m; i ++) {
int t = q[i].t, l = q[i].l, len = q[i].len;
v1[l].push_back(len - dep[t]);
v2[t].push_back(len - dep[t]);
}
memset(QAQ,0,sizeof(QAQ));
dfs_2(1);
for(int i = 1; i <= m; i ++) {
if(dep[q[i].s] - dep[q[i].l] == w[q[i].l])
ans[q[i].l] --;
}
for(int i = 1; i <= n; i ++) out(ans[i]), putchar(' ');
}
}
int main() {
n = read(), m = read();
for(int i = 1; i < n; i ++) {
int u = read(), v = read();
ins(u, v), ins(v, u);
}
for(int i = 1; i <= n; i ++) w[i] = read();
dfs1(1), dfs2(1, 1);
pts_6::solve();
}
(实际上树剖那里只保留三个就好不过我懒得删了qwq)
然后放上长达9kb的有所有部分分做法的代码
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define il inline
namespace io {
#define in(a) a=read()
#define out(a) write(a)
#define outn(a) out(a),putchar('
')
#define I_int int
inline I_int read() {
I_int x = 0, f = 1; char c = getchar();
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
char F[ 200 ] ;
inline void write( I_int x ) {
if( x == 0 ) { putchar( '0' ) ; return ; }
I_int tmp = x > 0 ? x : -x ;
if( x < 0 ) putchar( '-' ) ;
int cnt = 0 ;
while( tmp > 0 ) {
F[ cnt ++ ] = tmp % 10 + '0' ;
tmp /= 10 ;
}
while( cnt > 0 ) putchar( F[ -- cnt ] ) ;
}
#undef I_int
}
using namespace io ;
using namespace std ;
#define N 300010
int siz[N], dep[N], top[N], fa[N], id[N];
int n, m, f[N], qwq[N], total[N * 2], QAQ[N * 3];
int cnt, head[N], w[N];
int ans[N];
struct edge {
int to, nxt;
}e[N<<1];
void ins(int u, int v) {
e[++cnt] = (edge) {v, head[u]};
head[u] = cnt;
}
namespace pts_1 {
void solve1() {
for(int i = 1; i <= m; i ++) {
int s = read(), t = read();
if(w[s] == 0) ans[s] ++;
}
for(int i = 1; i <= n; i ++) out(ans[i]), putchar(' ');
}
void solve2() {
for(int i = 1; i <= m; i ++) {
int s = read(), t = read();
ans[s] ++;
}
for(int i = 1; i <= n; i ++) out(ans[i]), putchar(' ');
}
}
namespace tree_chain {
void dfs1(int u) {
siz[u] = 1;
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
fa[e[i].to] = u;
dep[e[i].to] = dep[u] + 1;
dfs1(e[i].to);
siz[u] += siz[e[i].to];
}
}
int tim;
void dfs2(int u, int topf) {
top[u] = topf;
id[u] = ++ tim;
int k = 0;
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
if(siz[e[i].to] > siz[k]) k = e[i].to;
}
if(!k) return;
dfs2(k, topf);
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u] || e[i].to == k) continue;
dfs2(e[i].to, e[i].to);
}
}
int lca(int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
return x;
}
struct tree {
int l, r, sum, add;
}t[N<<2];
#define mid ((l + r) >> 1)
#define lc (rt << 1)
#define rc (rt << 1 | 1)
void build(int l, int r, int rt) {
t[rt].l = l; t[rt].r = r;
if(l == r) return;
build(l, mid, lc); build(mid + 1, r, rc);
}
void pushup(int rt) {t[rt].sum = t[lc].sum + t[rc].sum;}
#define l t[rt].l
#define r t[rt].r
void pushdown(int ln, int rn, int rt) {
if(t[rt].add) {
int &x = t[rt].add;
t[lc].sum += x * ln; t[rc].sum += x * rn;
t[lc].add += x; t[rc].add += x;
x = 0;
}
}
void upd(int L, int R, int c, int rt) {
if(L <= l && r <= R) {
t[rt].sum += c * (r - l + 1);
t[rt].add += c;
return;
}
pushdown(mid - l + 1, r - mid, rt);
if(L <= mid) upd(L, R, c, lc);
if(R > mid) upd(L, R, c, rc);
pushup(rt);
}
int query(int L, int R, int rt) {
if(L <= l && r <= R) return t[rt].sum;
pushdown(mid - l + 1, r - mid, rt); int ans = 0;
if(L <= mid) ans += query(L, R, lc);
if(R > mid) ans += query(L, R, rc);
return ans;
}
#undef lc
#undef rc
#undef l
#undef r
#undef mid
}
using namespace tree_chain;
namespace pts_2 {
void solve() {
for(int i = 1; i <= m; i ++) {
int s = read(), t = read();
int l = lca(s, t), tot = 0;
for(int k = s; k != l; k = fa[k]) {
if(w[k] == tot) ans[k] ++;
++tot;
}
if(w[l] == tot) ans[l] ++;
tot += dep[t] - dep[l];
for(int k = t; k != l; k = fa[k]) {
if(w[k] == tot) ans[k] ++;
--tot;
}
}
for(int i = 1; i <= n; i ++) out(ans[i]), putchar(' ');
}
}
void add(int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
upd(id[top[x]], id[x], 1, 1);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
upd(id[x], id[y], 1, 1);
}
namespace pts_3 {
void solve() {
for(int i = 1; i <= m; i ++) {
int s = read(), t = read();
add(s, t);
}
for(int i = 1; i <= n; i ++) {
if(w[i] == dep[i]) {
ans[i] = query(id[i], id[i], 1);
}
}
for(int i = 1; i <= n; i ++) {
out(ans[i]), putchar(' ');
}
}
}
namespace pts_5 {
//链的情况
//要么s>t 要么s <= t
//考虑s <= t
//对于s -> t路径上的i,只有i - s = w[i]时才有贡献
//i-w[i]=s
//设f[i]=i-w[i]
//即s=f[i]时,才有贡献
//s > t同理
//所以对于一个点i,对它有贡献的点一定是起点为i-w[i]/i+w[i]且终点过i的路径的个数
vector<int> G[N];
void solve() {
for(int i = 1; i <= m; i ++) {
int S = read(), T = read();
G[S].push_back(T);
}
for(int i = 1; i <= n; i ++) {
int tot = 0;
if(i - w[i] > 0)
for(int j = 0, len = G[i - w[i]].size(); j < len; j ++) {
if(G[i - w[i]][j] >= i) tot ++;
}
if(i + w[i] <= n)
for(int j = 0, len = G[i + w[i]].size(); j < len; j ++) {
if(G[i + w[i]][j] <= i) tot ++;
}
ans[i] = tot;
}
for(int i = 1; i <= n; i ++) out(ans[i]), putchar(' ');
}
}
namespace pts_4 {
// t = 1
// dep[s]-dep[i]=w[i]则有贡献
// 即 dep[s]=w[i]+dep[i]
void dfs(int u) {
if(qwq[u]) total[dep[u]] += qwq[u];
int t = total[f[u]];
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
dfs(e[i].to);
}
ans[u] = total[f[u]] - t;
}
void solve() {
for(int i = 1; i <= n; i ++) f[i] = w[i] + dep[i];
for(int i = 1; i <= m; i ++) {
int s = read(), t = read();
qwq[s]++;
}
dfs(1);
for(int i = 1; i <= n; i ++) {
out(ans[i]), putchar(' ');
}
}
}
namespace pts_6 {
struct ques {
int s, t, l, len;
} q[N];
vector<int>v1[N*2], v2[N*2], v3[N * 2];
int Max_dep = 0;
//对于u->lca(u,v)
//同链做法
void dfs_1(int u) {
int now = w[u] + dep[u] + 300000, t = total[now];
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
dfs_1(e[i].to);
}
total[dep[u] + 300000] += qwq[u];
ans[u] += total[now] - t;
for(int i = 0, len = v3[u].size(); i < len; i ++) total[dep[v3[u][i]] + 300000] --;
}
//对于lca(u,v) -> v
//可得式子:
//dep[t]-dep[i] = len - w[i]
//移项得
//dep[t] - len = dep[i] - w[i]
void dfs_2(int u) {
int now = w[u] - dep[u] + 300000;
int t = QAQ[now];
for(int i = head[u]; i; i = e[i].nxt) {
if(e[i].to == fa[u]) continue;
dfs_2(e[i].to);
}
for(int i = 0, len = v2[u].size(); i < len; i ++) QAQ[300000 + v2[u][i]] ++;
ans[u] += QAQ[now] - t;
for(int i = 0, len = v1[u].size(); i < len; i ++) QAQ[300000 + v1[u][i]] --;
}
void solve() {
for(int i = 1; i <= n; i ++) Max_dep = max(Max_dep, dep[i]);
for(int i = 1; i <= m; i ++) {
int s = read(), t = read(), l = lca(s, t);
int len = dep[s] + dep[t] - 2 * dep[l];
q[i] = (ques) {s, t, l, len};
v3[l].push_back(s); qwq[s] ++;
}
dfs_1(1);
for(int i = 1; i <= m; i ++) {
int t = q[i].t, l = q[i].l, len = q[i].len;
v1[l].push_back(len - dep[t]);
v2[t].push_back(len - dep[t]);
}
memset(QAQ,0,sizeof(QAQ));
dfs_2(1);
for(int i = 1; i <= m; i ++) {
if(dep[q[i].s] - dep[q[i].l] == w[q[i].l])
ans[q[i].l] --;
}
for(int i = 1; i <= n; i ++) out(ans[i]), putchar(' ');
}
}
int main() {
n = read(), m = read();
for(int i = 1; i < n; i ++) {
int u = read(), v = read();
ins(u, v), ins(v, u);
}
for(int i = 1; i <= n; i ++) w[i] = read();
if(n == 991 && m == 991) {pts_1::solve1(); return 0;}
if(n == 992 && m == 992) {pts_1::solve2(); return 0;}
dfs1(1), dfs2(1, 1);
if(n == 993 && m == 993) {pts_2::solve(); return 0;}
if(n == 99995 && m == 99995) {build(1, n, 1); pts_3::solve(); return 0;}
if(n == 99996 && m == 99996) {pts_4::solve(); return 0;}
if(n == 99994 && m == 99994) {pts_5::solve(); return 0;}
pts_6::solve();
}