【本文链接】
http://www.cnblogs.com/hellogiser/p/interview-questions-quickstart-for-combination-permutation.html
1. 只宠物合成,1只有 5技能,1 只有4 技能,每个技能有 a%概率遗传,请问刚好有7 个技能遗传成功的概率是?
7=5+2=4+3=3+4
只有
第一只5个技能 + 第二只2个技能:(a%)^7*C(5,5)*C(4,2)
第一只4个技能 + 第二只3个技能:(a%)^7*C(5,4)*C(4,3)
第一只3个技能 + 第二只4个技能:(a%)^7*C(5,3)*C(4,4)
加起来就可以了。
2. 某小组有四位男性和两位女性,六人围成一圈跳集体舞,不同排列方法有多少种?
答案: A(6,6)/6 = 5!=120
 =720种方法。但注意到下图显示的六种情况对应着相同的相对位置,应该将相同情况别除。所以共有720÷6=120种方法。
=720种方法。但注意到下图显示的六种情况对应着相同的相对位置,应该将相同情况别除。所以共有720÷6=120种方法。
[注释]N人排成一圈,有A(n,n)/n=(n-1)!种排法。题干中的“男女”为干扰条件。
3. 1-9这9个数字中,选3个出来,其和为奇数的组合有几个?
4. 字符串“alibaba”有?个不同的排列。
用概率的办法可以直接求解出C73*C42*A22,C73,7是下标,3是上标,结果是420;
5.在如下8*6的矩阵中,请计算从A移动到B一共有多少种走法?要求每次只能向上或着向右移动一格,并且不能经过P
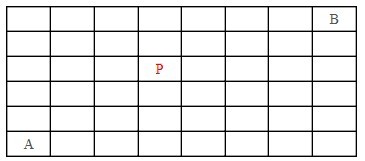
分析:
每个方格看做一个点,得到下面坐标图:

首先从A到B总共有c(7+5,5)种走法,从A到P有c(3+3,3)种走法,从P到B有c(4+2,2)种走法。
所以不经过点P得走法共有c(12,5)-(c(6,3)*c(6,2))种,即492种,选A。
http://www.cnblogs.com/legendmaner/archive/2013/04/18/3029573.html
计算组合数代码如下
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
#include "stdafx.h"
#include <iostream> using namespace std; int c(int n, int m) { if (m > n) return 0; if(m == n || m == 0) return 1; return c(n - 1, m) + c(n - 1, m - 1); } int main() { int ret = c(12, 5) - c(6, 3) * c(6, 2); // 492 cout << ret << endl; return 0; } |
6 爸爸,妈妈,妹妹,小强,至少两个人同一生肖的概率是多少?
答案:1-12*11*10*9/12*12*12*12 = 1-55/96 = 41/96