A Knight's Journey
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 47516 | Accepted: 16161 |
Description
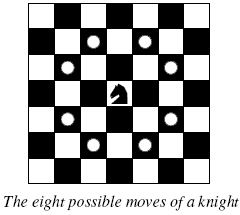 Background
Background The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
Input
The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .
Output
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
If no such path exist, you should output impossible on a single line.
Sample Input
3 1 1 2 3 4 3
Sample Output
Scenario #1: A1 Scenario #2: impossible Scenario #3: A1B3C1A2B4C2A3B1C3A4B2C4
题意:在一个n*m的国际棋盘上,象棋以马走日的方式走,行数为1-n的数字,列数为A-A+m的字母,按照字典序输出一条合适的路径。
思路:先构造一个棋盘数组和一个标记数组,按照字典序的方式就是先走字典序优先的位置,所以在定义方向数组的时候需要留意方位顺序,最后,每个样例后都一个空行。
喵?喵?喵?这道题的字典序操作真是毁我青春,我一直以为字典序就是先按照字母表顺序输出一遍再从头开始,然后就躺尸在这道题上,今天师父一看我屏幕,感叹这种水题居然还没有写过(毕竟上个周我就缠着师父给我讲为啥错了),最后师父才发现,原来我徒弟连字典序都不会(呜呜呜,谁知道是这样的字典序啊,样例误导人~),师父讲完字典序以后我就A过啦~
#include<stdio.h> #include<string.h> #define N 100 int map[N][N],m,n,flag; char str[N][N]; struct node1{ int x; char y; }l[N*N]; struct node2{ int x; char y; }f[N*N]; void dfs(int x,int y,int step) { int k[8][2] = {-1,-2,1,-2,-2,-1,2,-1,-2,1,2,1,-1,2,1,2}; int nx,ny,i; if(step > n*m)//在找到合适路径的情况下 { flag = 1; for(i = 1; i <= n*m; i ++) { f[i].x = l[i].x ;//将临时数组的值存入最终数组 f[i].y = l[i].y ; } return; } else { for(i = 0; i < 8; i ++) { if(!flag)//在未找到合适路径的情况下 { nx = x + k[i][0]; ny = y + k[i][1]; if(nx < 1||ny < 1||nx > n||ny > m||map[nx][ny] == 1) continue; map[nx][ny] = 1;//标记为已经访问过 l[step].x = nx;//用临时数组存储下标 l[step].y = str[nx][ny]; dfs(nx,ny,step +1);//往下搜索 map[nx][ny] = 0;//回溯 } } } } int main() { int i,j; int t,t2=0; scanf("%d",&t); while(t --) { scanf("%d%d",&n,&m); flag = 0; memset(map,0,sizeof(map));// memset(l,0,sizeof(l));// memset(f,0,sizeof(f));//初始化 for(i = 1; i <= n; i ++) { char ch = 'A'; for(j = 1; j <= m; j ++) str[i][j] = ch ++; } l[1].x = 1; l[1].y = 'A'; map[1][1] = 1;//将初识下标初始化为访问过 dfs(1,1,2); printf("Scenario #%d: ",++t2); if(!flag) printf("impossible "); else { for(i = 1; i <= n*m; i ++) printf("%c%d",f[i].y ,f[i].x ); printf(" "); } } return 0; }