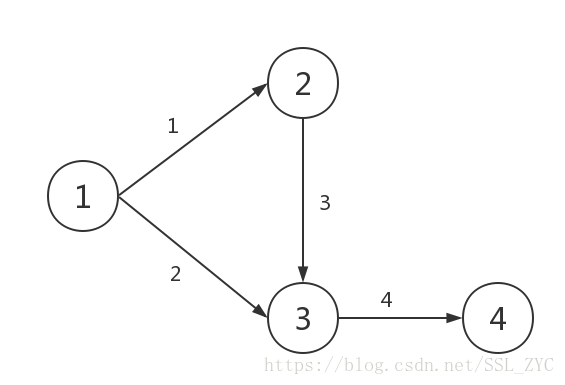
题目大意:
若一个点有条出边,则走每条出边的概率均为。给出一个有向无环图,求从起点走到终点的所经过的路径总长度期望。
4 4
1 2 1
1 3 2
2 3 3
3 4 4
7.00思路:
这很明显是一道数学期望的题目。但是由于之前没有做过这类的题目,所以做起来还是很吃力。
拿样例来说
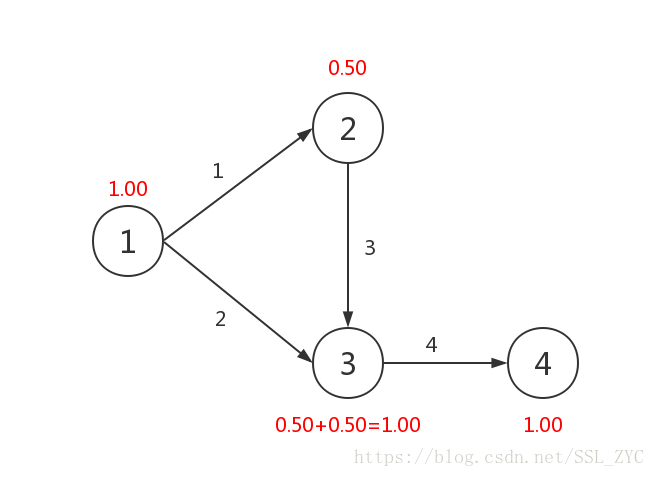
点一开始肯定是有1.00的几率到达的,它有两条出边,分别到达点和点,那么,点和点就各有0.50的几率到达。
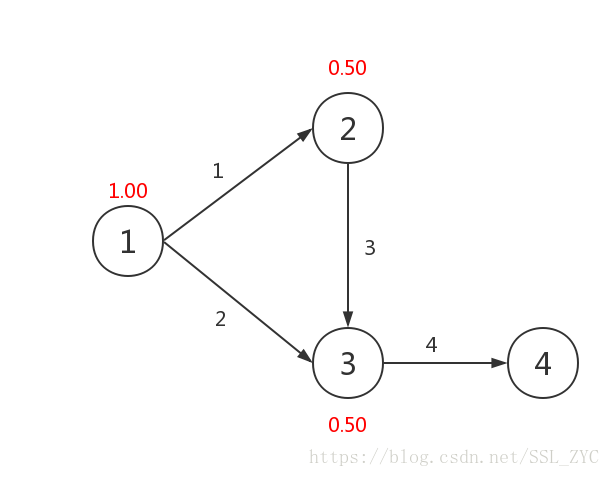
那么,点又有一条出边到达点,那么点到达的几率就在原来的基础上又加上了点的到达几率,所以点的到达几率为1.00。
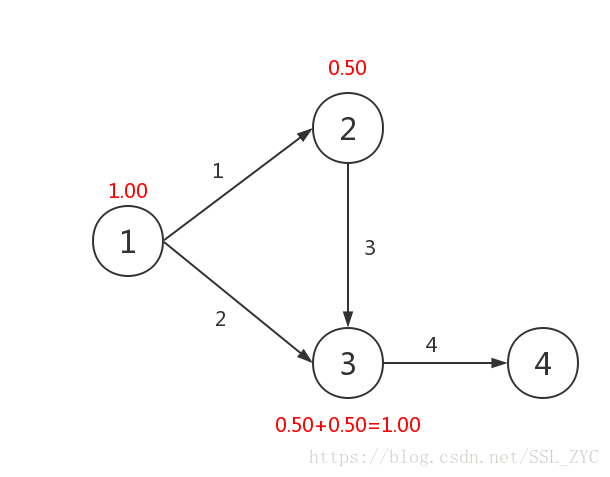
然后点就只有一条出边,通向点,所以点到达几率就为。
每次当我们访问到一个点时,就讲答案加上它到达的概率边权,即
且这个点的期望也要加上
然后继续向下搜索,搜到点时就返回,然后将期望值减去,防止重复计算。
代码:
#include <cstdio>
#include <iostream>
using namespace std;
int n,m,x,y,t;
double z,sum,s[300011],num[300011],head[300011],k;
struct edge //邻接表
{
int to,next;
double dis;
}e[500011];
void add(int from,int to,double d) //建边
{
t++;
e[t].dis=d;
e[t].to=to;
e[t].next=head[from];
head[from]=t;
}
void dfs(int x)
{
if (x==n) return; //到达终点
for (int i=head[x];i;i=e[i].next)
{
int v=e[i].to;
double l=s[x]/num[x]; //计算路径长度期望
s[v]+=l; //加上期望
sum+=e[i].dis*l; //答案
dfs(v);
s[v]-=l; //减掉期望
}
}
int main()
{
scanf("%d%d",&n,&m);
for (int i=1;i<=m;i++)
{
scanf("%d%d%lf",&x,&y,&z);
add(x,y,z); //建边
num[x]++;
}
s[1]=1.00;
dfs(1);
printf("%0.2lf\n",sum);
return 0;
}