题目大意:
题目链接:
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=41
https://www.luogu.org/problemnew/show/SP898
以雷达心为圆心的半圆形雷达覆盖范围有多个点,雷达可旋转,求最多覆盖数(含在边界的)。
思路:
叉积基础题。
首先很明显的可以先把不在雷达范围之内的点忽略掉。可以在读入时求出该点到雷达的距离,如果在半径之内才加入点集。
然后考虑对于每一个点,如果以雷达位置和点所在直线为半圆(雷达扫描面积)的直径所在直线,那么只有两种可能。
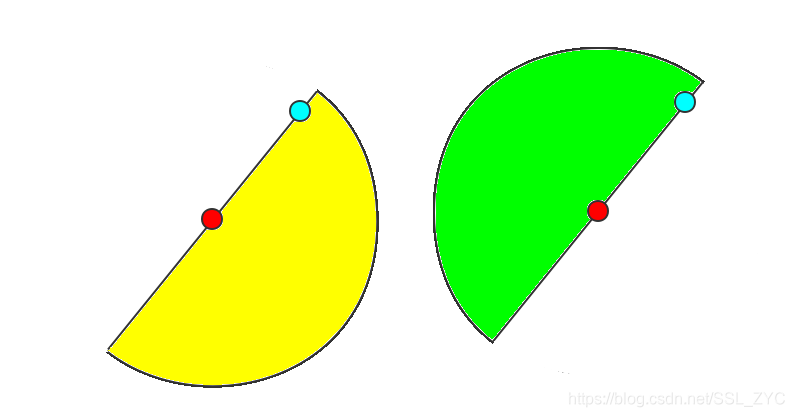
而其他的任意一点,要么会在黄色区域,要么会在绿色区域,要么就是在该直线上(即两个区域都属于)。
如果属于黄色区域,那么在以雷达(红色)为原点的平面直角坐标系中,和的叉积就会,如果在绿色区域叉积就会。(如果在直线上,叉积,两边都会计算)。
然后取个就可以了。
代码:
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int N=1010;
int n,m,ans,s1,s2;
double x,y,xx,yy,r;
struct node
{
double x,y;
}a[N];
double cal(double x1,double y1,double x2,double y2) //勾股求距离
{
return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
int main()
{
while (scanf("%lf%lf%lf",&x,&y,&r)==3&&r>=0.0)
{
n=0;
scanf("%d",&m);
for (int i=1;i<=m;i++)
{
scanf("%lf%lf",&xx,&yy);
if (cal(x,y,xx,yy)<=r) //在雷达范围内
{
a[++n].x=xx-x;
a[n].y=yy-y; //切记直接减去雷达所在位置。因为是以雷达为原点的平面直角坐标系。
}
}
ans=0;
for (int i=1;i<=n;i++)
{
s1=s2=0;
for (int j=1;j<=n;j++)
{
if (a[i].x*a[j].y-a[j].x*a[i].y>=0.0) s1++;
if (a[i].x*a[j].y-a[j].x*a[i].y<=0.0) s2++; //叉积
}
ans=max(ans,max(s1,s2));
}
printf("%d
",ans);
}
return 0;
}