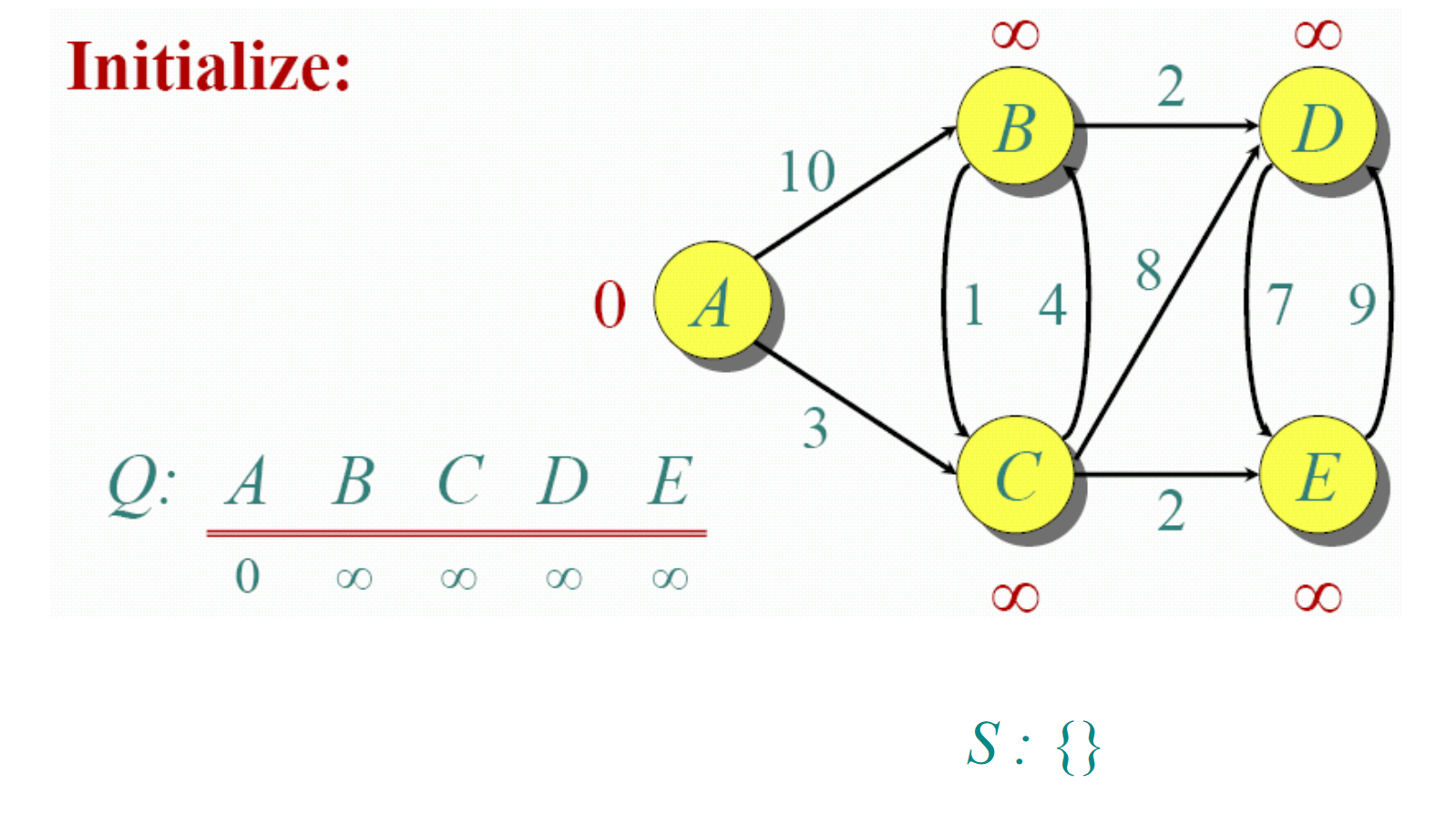
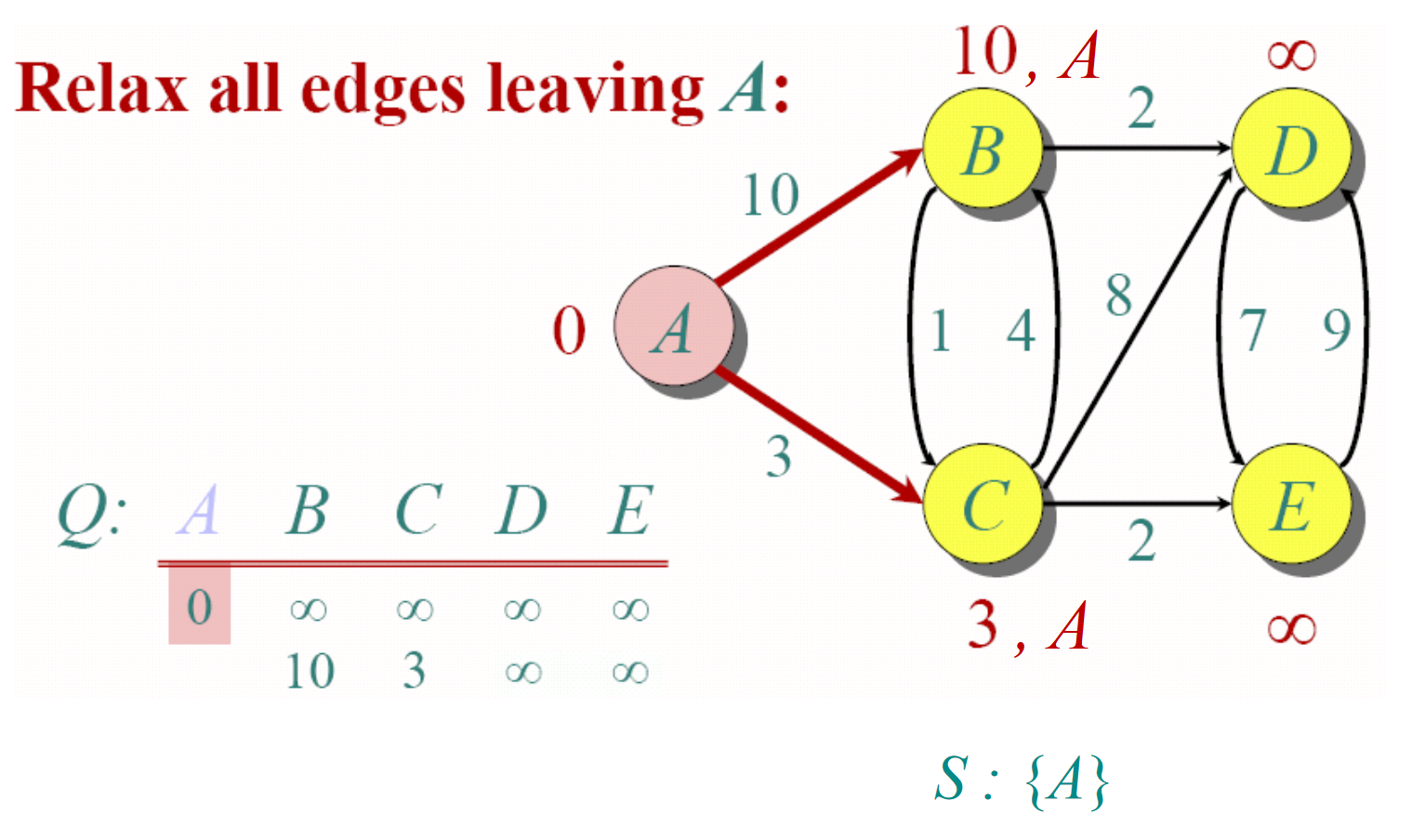
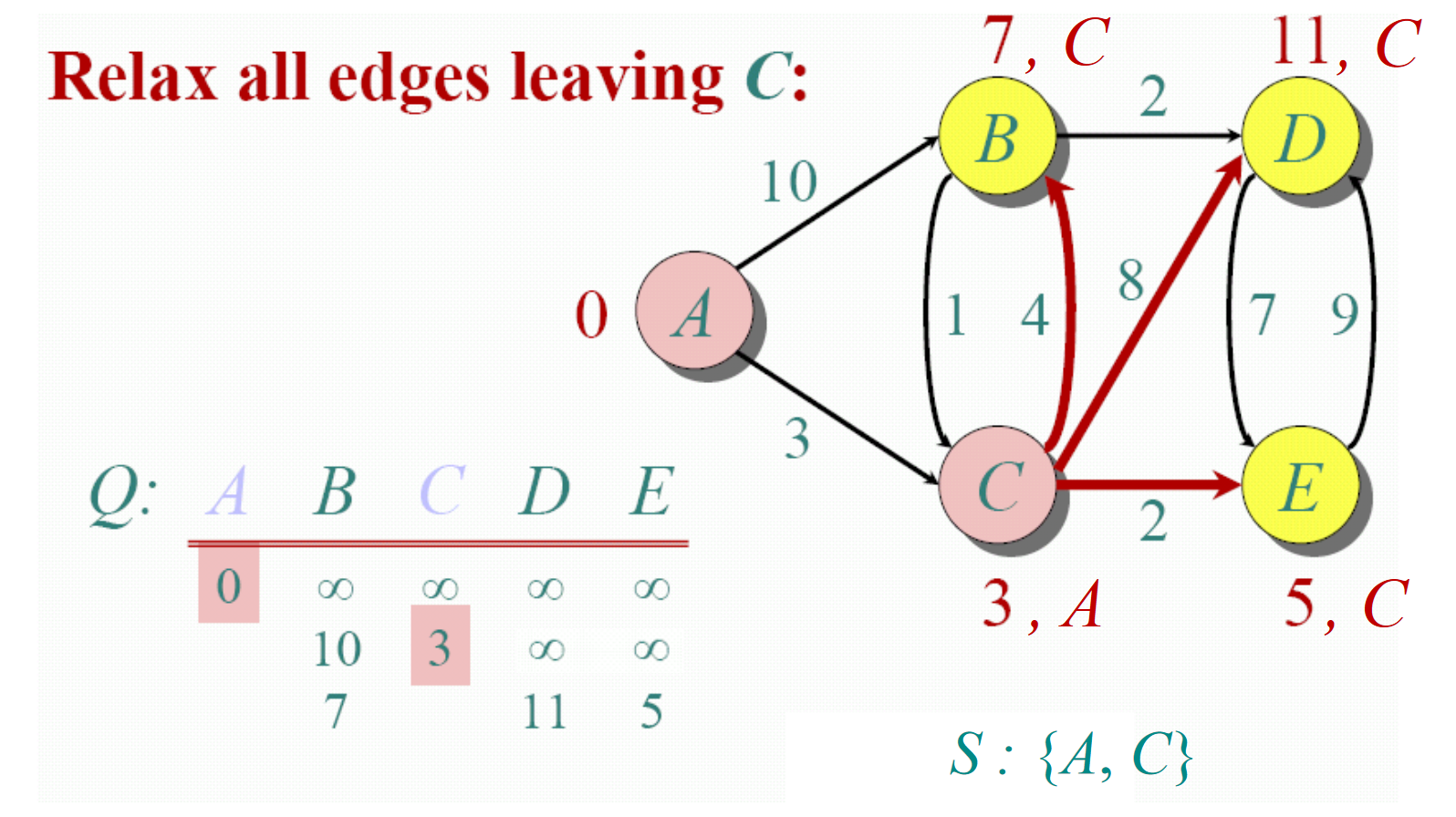
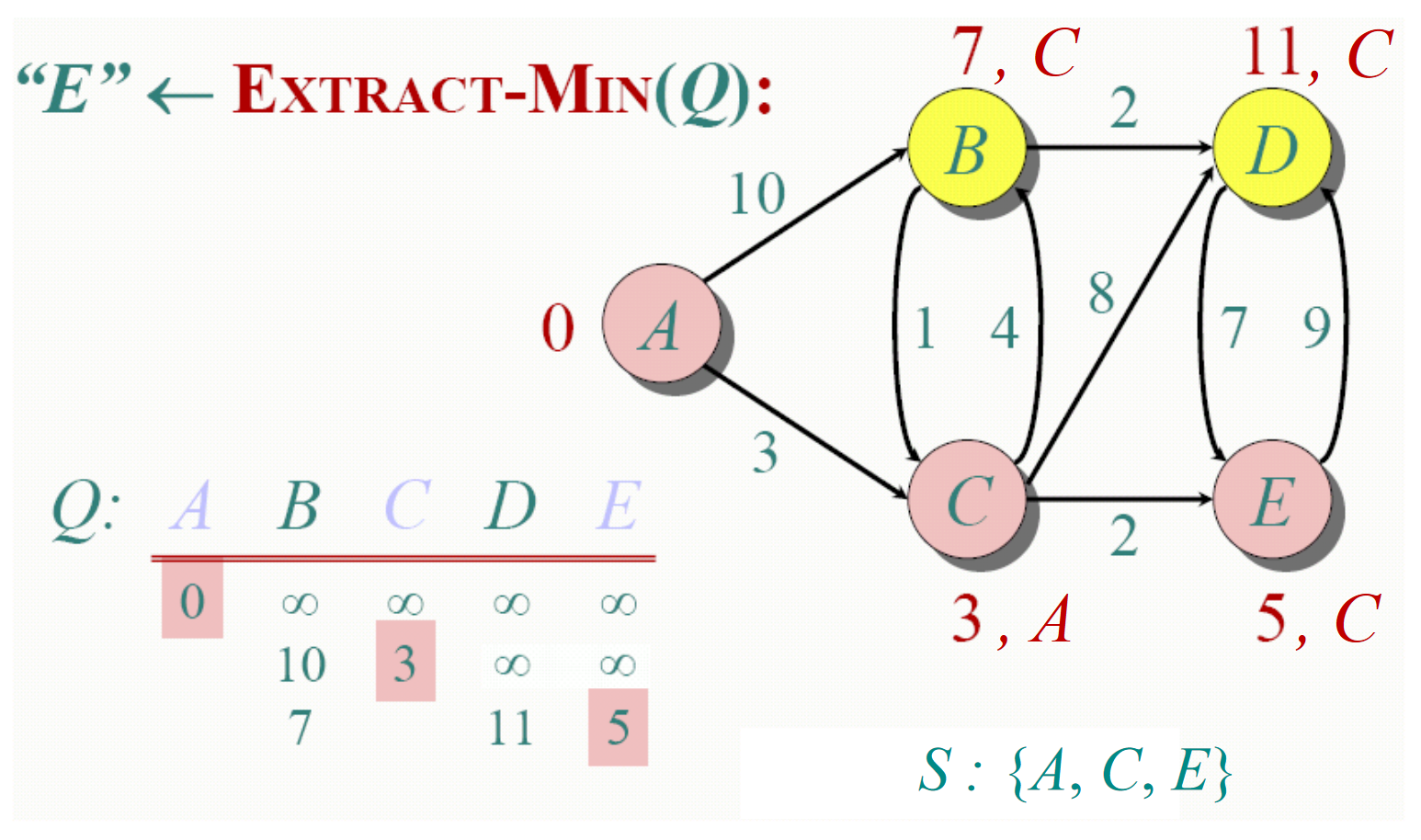
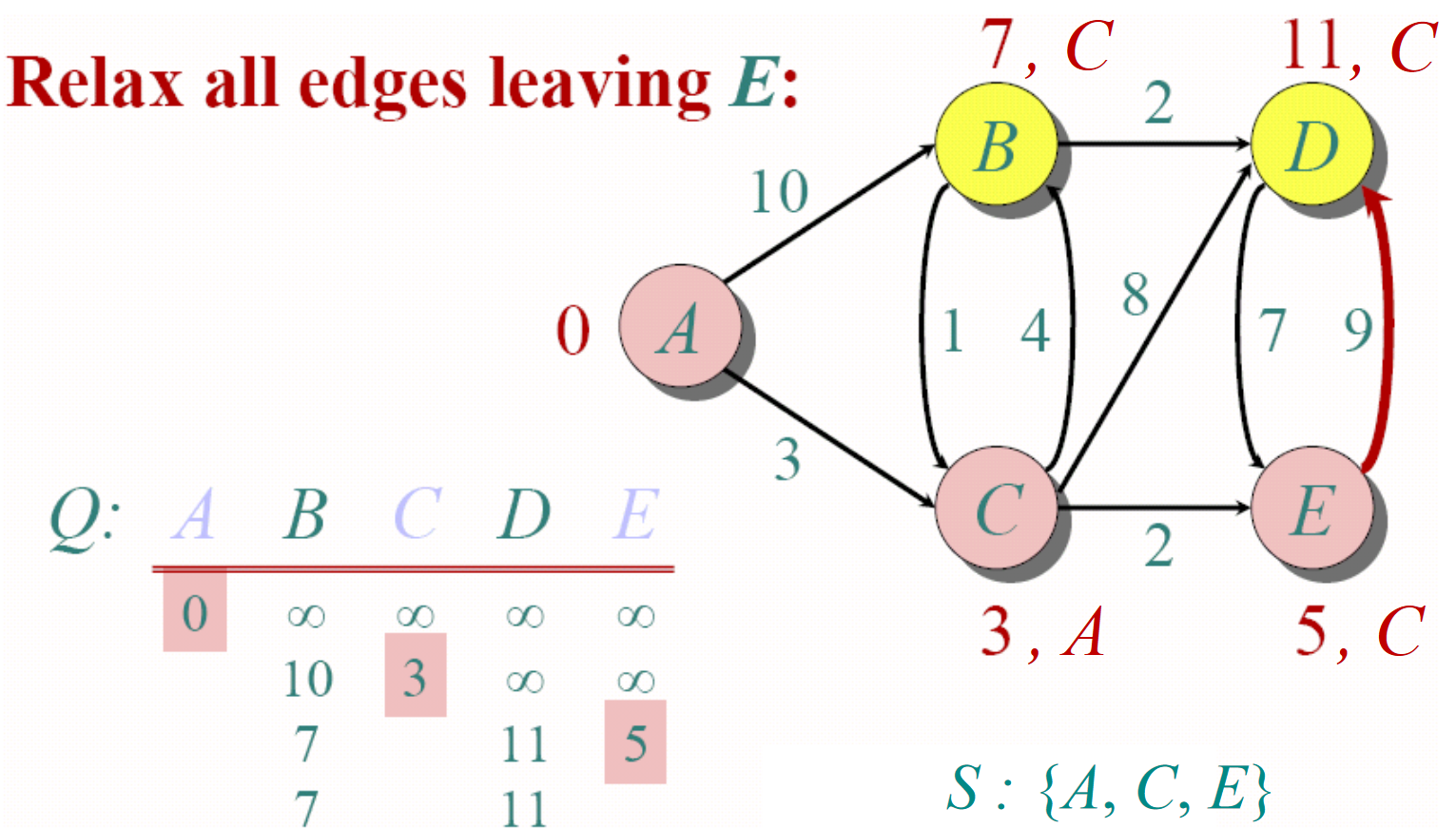
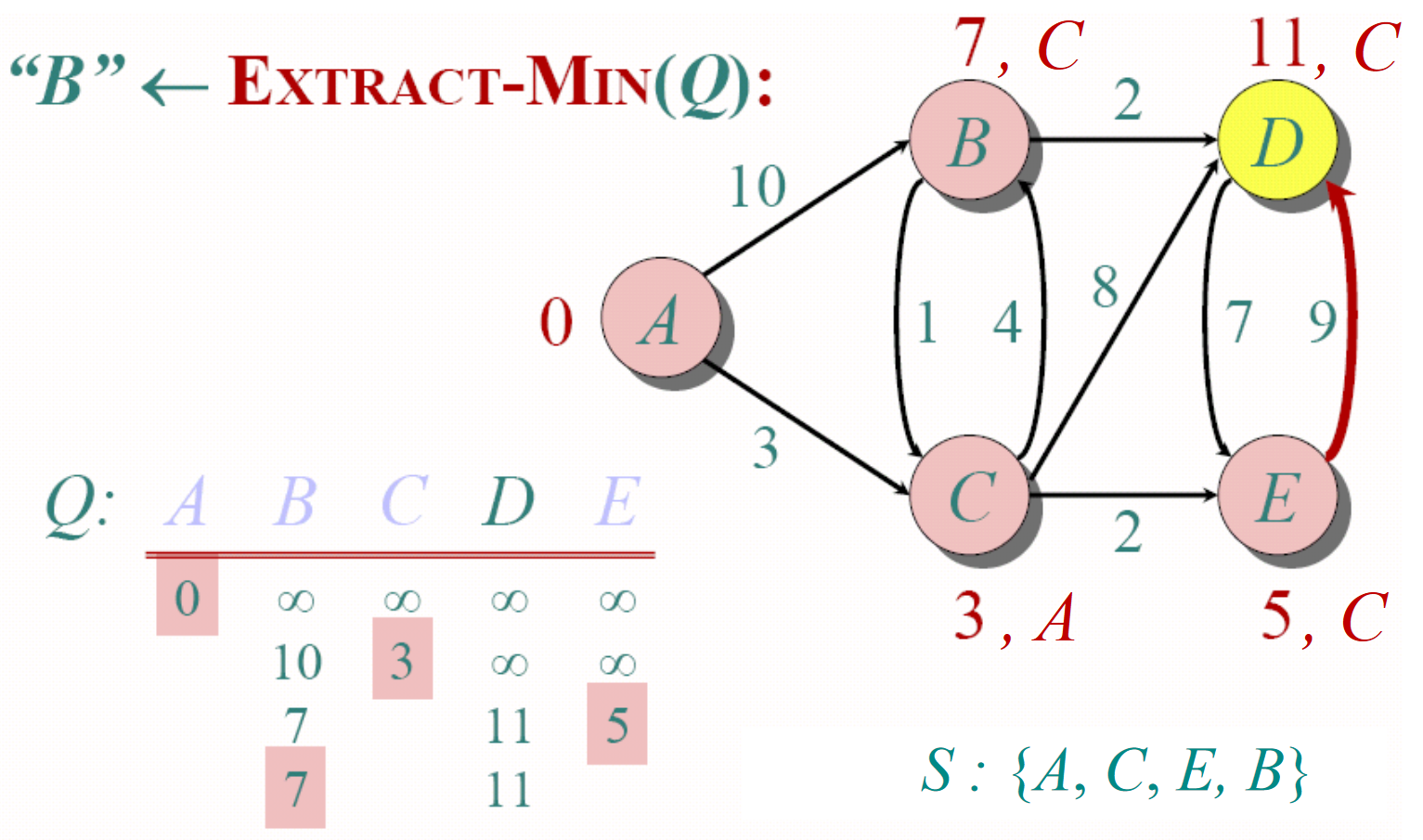
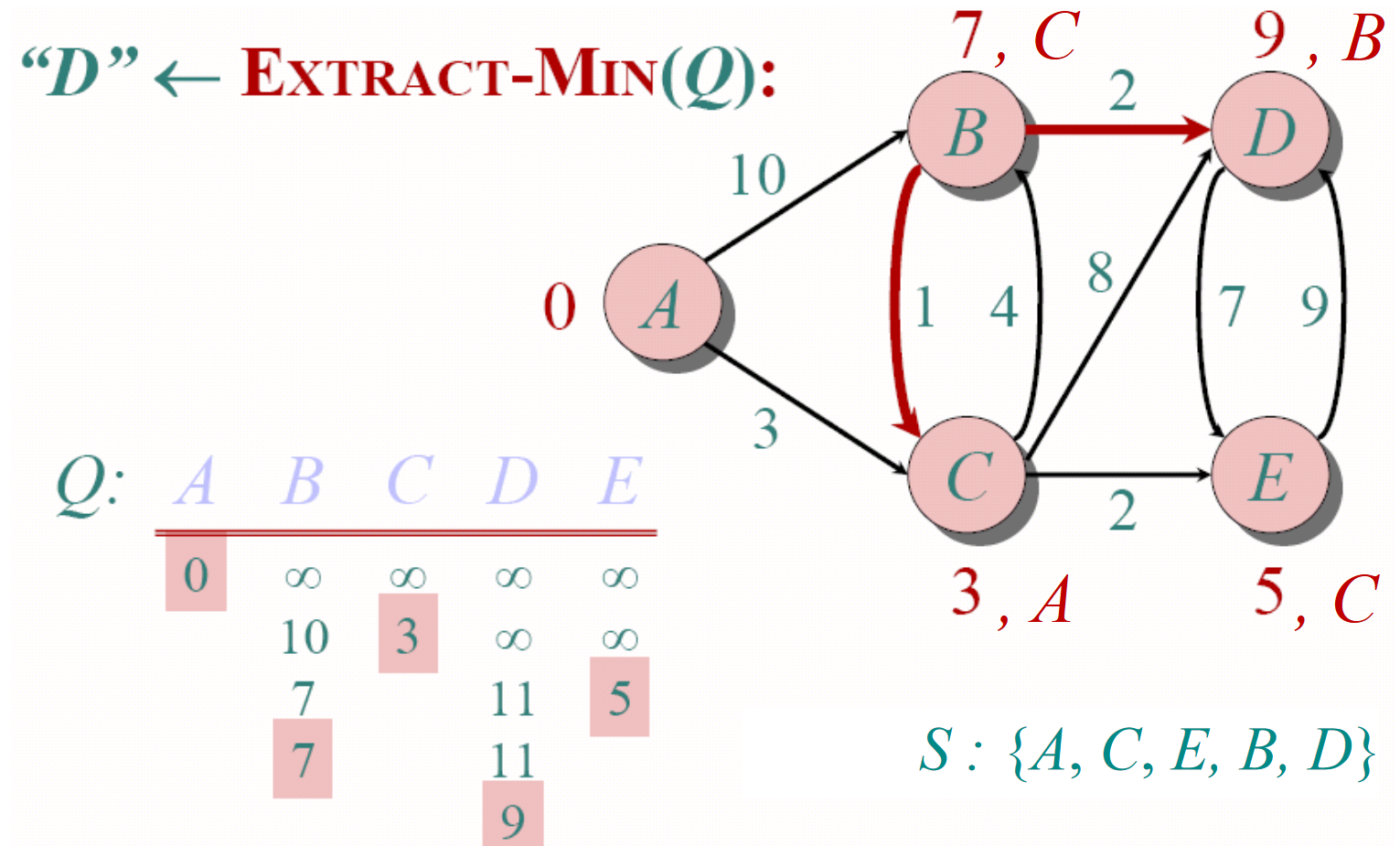
Dijkstra算法实际上是一个贪婪算法(Greedy algorithm)。因为该算法总是试图优先访问每一步循环中距离起始点最近的下一个结点。Dijkstra算法的过程如下图所示。

初始化
- 给定图中的一个结点
s作为起始点。 - 给定一个数组
dist[]存储图中所有结点到s的距离。将dist[s]初始化为0。对于图中的其他结点v,初始化dist[v]为无穷大。初始化为无穷大的意义在于我们假设其余所有结点在当前情况下尚未与s联通。随着算法的执行,dist[v]会保存图中从s到v的最短路径的距离。 - 给定一个minimum Heap,记为
Q。堆顶为当前情况下距离s最近的结点及相应的距离。将(s, 0)放入堆中。 - 给定一个Set,记为
S,保存所有已经访问过的结点。Set初始为空。基于Dijkstra算法的性质,我们总是以最短的路径遍历每一个结点,因此对于任一结点,一旦我们已经访问过,就代表着我们已经得到了从s到达这一结点的最短路径。
计算最短路径
- 当
Q不为空的情况下,取出堆顶的元素(v, [dist[v])—— 也就是当前距离s最近的结点v,及其距离dist[v]。 - 如果
v在S中,则代表我们已经访问过v的最短路径。那么跳过当前v,重复步骤1。 - 否则,将
v放在S中。 - 对于每一个与
v相邻的结点t:
- 如果
dist[v] + weight(v, t) < dist[t],则更新dist[t] = dist[v] + weight(v, t)。同时将(t, dist[t])放进Q中。 - 否则,不做任何处理。
- 如果
当算法结束后,dist[]中保存图中每一个除s之外的结点到s的最短路径的权重值(或长度)。如果从s到v不存在联通的路径,则dist[v] = ∞。
证明算法正确性
假设对于每个已经访问过的结点v,dist[v]存储从起始点s到v的最短路径。
当算法初始化时,dist[]中只包含dist[s] = 0,其正确性显而易见。
对于其余n-1个结点,假设u已经被访问且v尚未被访问,同时u和v之间存在一条边u -> v,其权重为weight(u,v),那么一定有dist[v] = dist[u] + weight(u, v)。否则的话,假设存在另一条更短的路径dist[t]满足dist[t] + weight(t, v),则根据上述算法,t一定先于u被访问,则与我们当前的假设产生了矛盾。该论断对于余下的所有结点都成立。
因此Dijkstra算法一定能给出从出发点到其余所有结点(在可以到达的情况下)的最短路径。
复杂度分析
设图中总计有E条边,N个结点。
时间复杂度:O(ElogE)。因为所使用的最小堆最大可达O(E)大小,同时我们从其中将每个元素取出来一次。
空间复杂度:O(N+E)。其中O(N)为存储dist所用空间。O(E)为存储图的邻接链表及最小堆所用空间。