『算法设计_伪代码』动态规划问题

这一部分伪代码太长，所以只讲解解题手段

核心思想是将复杂问题化解为两个简单一点的问题，递归处理。

零、几个概念

最优子结构

一个问题的最优解包含其子问题的最优解

证明：反证法，a=b+c中a的最优解如果不是b和c的最优解，则b和c的最优解和将优于a的最优解，矛盾，的证。

重叠子问题

解决问题的递归算法中会重复求解相同的子问题

解法：对每个子问题的第一次求解存入表中，再次求解时直接查询即可。

一、割绳子问题

r：表示最大价值

s：表示此时分割位置，如i=8时的2表示绳子分为2、6两段，2、6对应i=2和i=6的r

二、矩阵链乘问题

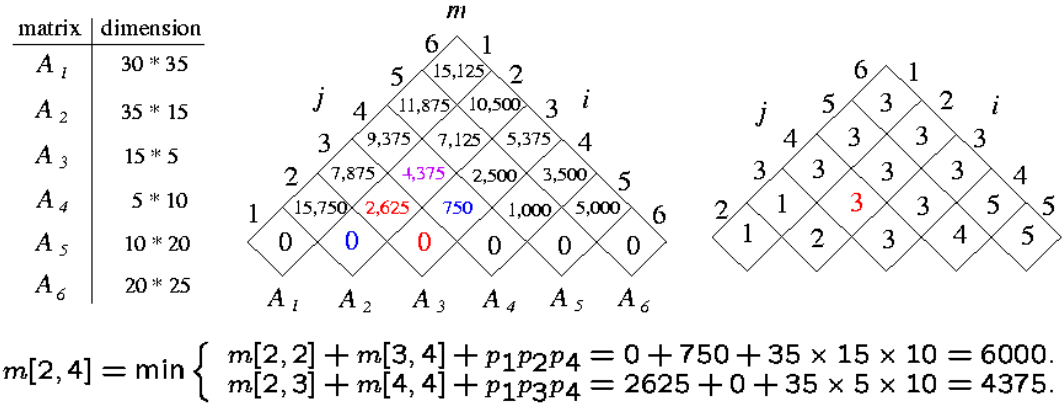
右表记录k值

pi表示Ai的第二维，pi-1表示Ai的第一维

三、最长公共子序列 (LCS)

问题描述

并不是通常意义上的公共子序列（和常见的算法题中的不一样），定义如下，

解法示意

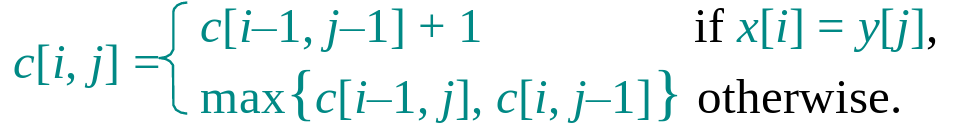
1. xi=yi时直接将当前的左上格子数+1作为本格，箭头指向左上；
2. xi!=yi时比较上方格子和左面格子：
   1. 上方不小于右侧，箭头指上，copy上方格子
   2. 否则箭头指右，copy右侧格子

 格子图生成先补0，然后由上到小一行一行的填充，而结果读取是从右下到左上的方向：

 四、最优二叉查找树

问题描述

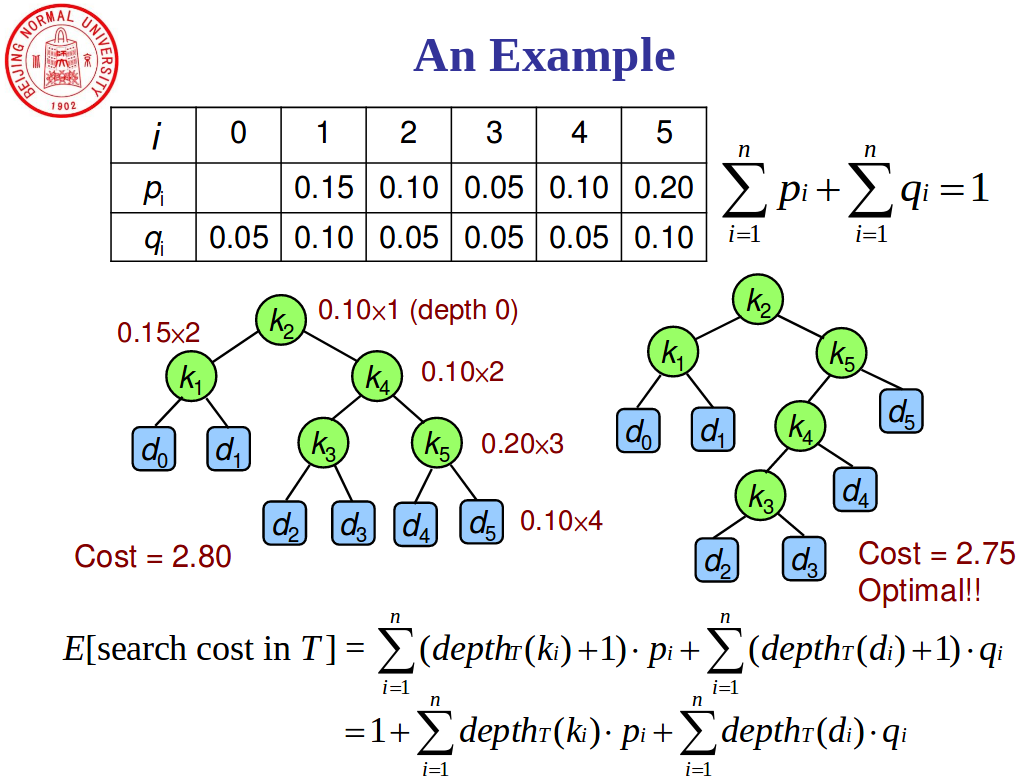
解法示意

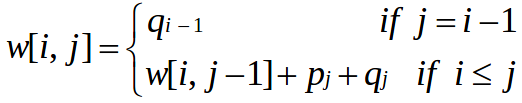
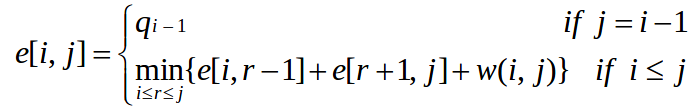
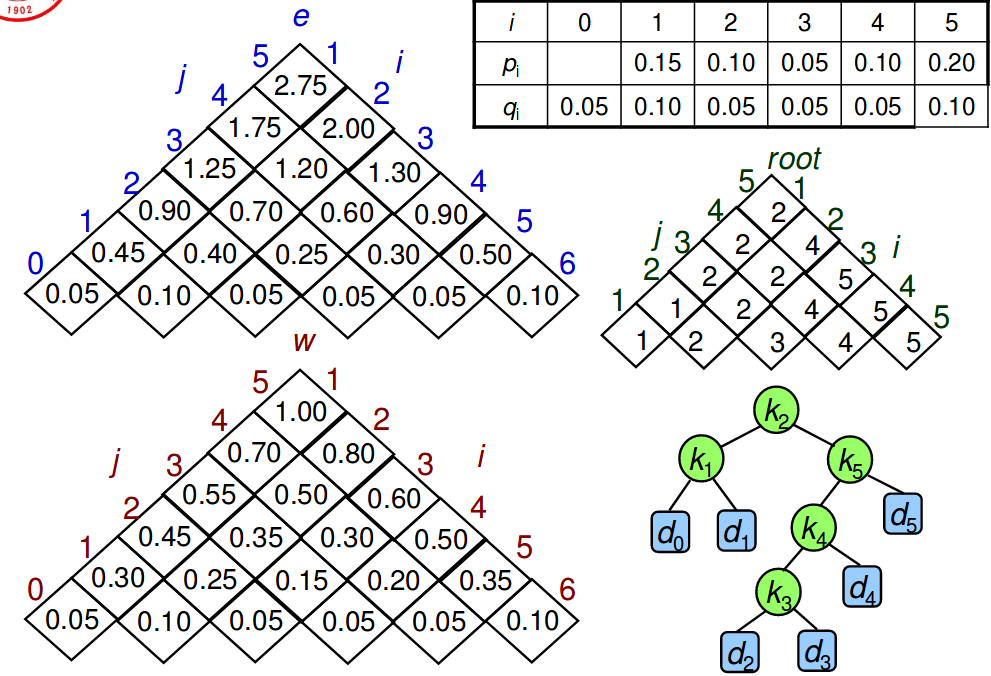
W为概率矩阵，e为消耗期望矩阵

先填W，后填e，注意表格行1:6,列0:5，root记录对应e位置的r的值。

重建时看root，[1,5]位置为2，表示2为根，分解为k1，{k3，k4，k5}，再看[3,5]为5，右子树5为根……