描述RSA的实现步骤介绍文章非常多，但说明并证明其原理，并进而讨论为什么这样设计的文章不多。本人才疏学浅，不敢说理解了R.S.A.三位泰斗的设计初衷，简单就自己的理解写一写，博大家一笑。
以下原创内容欢迎网友转载，但请注明出处： https://www.cnblogs.com/helesheng
一、用到的数论基础定理
R.S.A.三位一定是数学大神欧拉的粉丝，因为所有用到的基本原理和定理都是以欧拉命名的。
1、欧拉函数
小于m的书中，所有与m互质的数的个数定义为“欧拉函数”，写为：Φ(m)。若m的质因数分解为： 
（其中Pi为素数，ei为正整数），Φ(m) 的计算公式为：
2、欧拉定理
若gcd(a,m)=1（a和m互质），则有：
启示：
1）欧拉定理是“环”到“域”的重要过渡，只要把左边的乘方运算拆为两个乘方运算的乘积，拆成的两个部分就可以理解为“域”中的“元”及其乘法“逆元”，这样环上的模逆元就存在了，“环”就可以变成“域”了。但需要注意的是欧拉定理存在的条件是gcd(a,m)=1这个条件。为满足这个条件，密码学（cryptology）如果工作在有限域上，经常会进行选择m为素数，或者非常接近素数的情况；而a则之需要是小于m的任意数，作为明文或密文。但严格说，RSA不是工作在伽罗瓦域上的，因为RSA的模数n是两个素数p、q的乘积。n很接近一个素数，在证明RSA时，需要专门证明gcd(a,n)不为1的情况。
2）费马小定理是欧拉定理的“特例中的特例”，其描述为：当p是一个素数时
， 或 
。证明：若p为素数gcd(a,p)=1；而欧拉函数Φ(m)=p-1。代入欧拉定理，即可得到费马小定理。
二、RSA过程
Step 1.选择两个大素数p和q，当n为7680位（960字节）的数时，p和q约为3072位，在这样长度的奇数中寻找一个素数的可能性约为：
即约1065个奇数中有一个素数。
计算n=p*q。
Step 2.计算n的欧拉函数Φ(n)。
因为n的两个质因数已知为p和q，代入公式（1）有Φ(n)=(p-1)(q-1)。
Step 3.选择一个与Φ(n)互质的数e。
a)要求e与Φ(n)互质的原因是要保证e的模n乘法逆的存在。而这个乘法逆就是私钥d。
b)e将作为公钥，e取值不大，一般有3、17、65537几种选择。因为公钥e远小于私钥d，持有公钥的一方，在不论是进行加密（用RSA做密钥交换）还是进行解密（用RSA作数字签名）的速度都远远快于持有私钥d的一方。
e之所以选择这几个数，除了是素数之外，还因为这几个数3（b101）、17（b1_0001）、65537（b1_0000_0001）的二进制表达中1的个数特别少，这样在计算xe时将会特别简便。
c)在整个RSA运算中，计算d是唯一一次使用Φ(n)作为模的地方，其他地方都是使用n作为模。
Step 4.使用公钥e和私钥d进行加解密
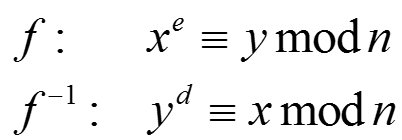
a）上面的公式中并没有指定x和y谁是明文谁是密文，也就是说两者都可以作为明文和密文。
b）RSA找到了一种“一一对应”的映射关系f：因为e较小，且公开，所以x映射到y很容易；y映射到x很困难，d较大，且不知道p、q时很难得到。这样的映射f被称为单向映射。
三、RSA的证明
证明RSA过程，等价于证明：
其中
n=p×q，n只有p、q两个质因数。
根据n和x的情况分两种情况讨论：
情况一：当x不含有p和q两个质因数时，n和x互质，gcd(n,x)=1。根据欧拉定理有：
根据d的定义，d和e对模Φ(n)互逆，有：
将上式写成另一种形式：
将其代入欲证明的(2)，有：
情况二：当n和x不互质时，由于n=p×q，x可以写成：x=r×p或s×q（但不能写成x=r×p×q，因为这会使得x > n）。不失一般性，假设x=r×p。由于
，根据欧拉定理和欧拉函数有：
根据d的定义，同样有(5)式，而（6）式则变为：
其中使用了欧拉函数计算公式
将（7）代入上式有：
至此，证明了不论在那种情况下都有 ，证毕！
四、RSA的设计思路
不自量力的揣测一下R.S.A.三位的设计思路，是利用欧拉定理构造了以n作为模的环上互逆的一对数x和y作为明文和密文，x和y各自是对方的e次方和d次方。如果知道n的质因数分解（p×q）的，可以通过欧拉函数方便的计算出e和d，否则只能靠对方告知其中之一，从而形成了单向映射，构成了所谓“非对称加密”。
另外，在e和d的复杂度的分割上，并不是相等的。设计者让知道质因数分解的一方的密钥d远远复杂于e，原因有二：其一，知道质因数分解的一方可以通过中国余数定理CRT加速计算；其二，不知道质因数分解的诸多“非对称”通信者，可以使用较低的算力执行加、解密。
较简单密钥e称为公钥，较复杂密钥d称为私钥。