转载自:https://www.zhihu.com/question/41252833/answer/141598211
仅从机器学习的角度讨论这个问题。
相对熵(relative entropy)就是KL散度(Kullback–Leibler divergence),用于衡量两个概率分布之间的差异。
对于两个概率分布 和
和 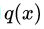 ,其相对熵的计算公式为:
,其相对熵的计算公式为:

(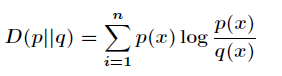 )
)
注意:由于 和
和 在公式中的地位不是相等的,所以
在公式中的地位不是相等的,所以
相对熵的特点,是只有 时,其值为0。若
时,其值为0。若 和
和 略有差异,其值就会大于0。其证明利用了负对数函数(
略有差异,其值就会大于0。其证明利用了负对数函数(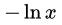 )是严格凸函数(strictly convex function)的性质。具体可以参考PRML 1.6.1 Relative entropy and mutual information.
)是严格凸函数(strictly convex function)的性质。具体可以参考PRML 1.6.1 Relative entropy and mutual information.
相对熵公式的前半部分 就是交叉熵(cross entropy)。
就是交叉熵(cross entropy)。
若 是数据的真实概率分布,
是数据的真实概率分布, 是由数据计算得到的概率分布。机器学习的目的就是希望
是由数据计算得到的概率分布。机器学习的目的就是希望 尽可能地逼近甚至等于
尽可能地逼近甚至等于 ,从而使得相对熵接近最小值0. 由于真实的概率分布是固定的,相对熵公式的后半部分
,从而使得相对熵接近最小值0. 由于真实的概率分布是固定的,相对熵公式的后半部分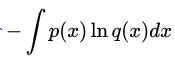 就成了一个常数。那么相对熵达到最小值的时候,也意味着交叉熵达到了最小值。对
就成了一个常数。那么相对熵达到最小值的时候,也意味着交叉熵达到了最小值。对 的优化就等效于求交叉熵的最小值。另外,对交叉熵求最小值,也等效于求最大似然估计(maximum likelihood estimation)。具体可以参考Deep Learning 5.5 Maximum Likelihood Estimation.
的优化就等效于求交叉熵的最小值。另外,对交叉熵求最小值,也等效于求最大似然估计(maximum likelihood estimation)。具体可以参考Deep Learning 5.5 Maximum Likelihood Estimation.