使用GAC加速 解决CSP问题 Kakuro

Kakuro - Cross Sums

问题如下 一个简单的例子

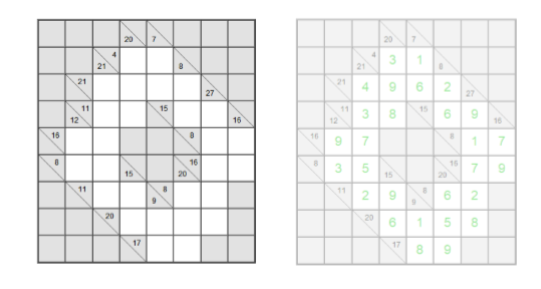
可以看出限制条件是某行或某列的某几个空白格子求和等于某个值，且每一个限制中的格子所填的数必须为1-9且互异。

直接暴力搜索，空白格子太多，复杂度是无法接受的。

我们考虑用GAC加速。

所谓GAC就是在填充一个变量的时候，保证和这个变量相关的所有限制的所有变量都是一致的！

什么是一致呢？ 就是对一个变量的论域内的所有可取的值，其他相关变量可以有一种取值满足限制条件。

如果我们在搜索的全过程都能满足GAC的一致性，那么每一步所选的变量，最后就可以是一个有效的解。

下面来解释一下具体的GAC搜索过程

初始状态，所有的变量论域都是满的，我们的目的是找到一个解，也就是说目标状态是这样的：

所有变量的论域中有且只有一个可选变量，同时满足GAC。根据GAC的定义，这显然就是CSP问题的解了。

如何从初始状态达到目标状态呢？ 显然就是删除变量论域中的可取值了（也就是对变量赋值）

每次选择一个变量，把目标值以外的其他值全部从论域中删除，然后进行GAC ，达到一致状态，然后继续选取变量，继续GAC...

有一点要注意，搜索是有回溯的，所以所有删除的论域取值都要进行标记，以便restore。

下面给出伪代码

对于15*15的数据，我的cpp代码运行效果如下

下面给出cpp代码 和6个测试数据

// Wang Bingsen 15336169 


#include<bits/stdc++.h>

using namespace std;
struct Variable
{
 bool Domain[10];
 int Row,Col,dsize;
 int Value;
 Variable()
 	{
 	 this->Value=0;
 	 this->dsize=9;
 	 memset(Domain,true,sizeof(Domain));
 	 Row=Col=-1;
	}	
};
struct Constrain
{
 bool Used[10];
 int Goal;
 vector<int>Scop;
 Constrain()
 	{
 	 memset(Used,false,sizeof(Used));
	 Goal=-1;	
	 Scop.resize(0);
	}	
 Constrain(int c)
 	{
 	 Scop.resize(0);
 	 memset(Used,false,sizeof(Used));
	 Goal=0;
	 this->Goal=c;
	}	
};

inline char getc();
void Init();
bool Support(int seted,Constrain & C);
bool GAC_Enforce(queue<int> & P,vector<pair<int,int> > & Restore);
void Reimburse(vector<pair<int,int> >& Re);
bool Set();
bool Solve();


vector<Variable> Var; 
vector<Constrain> Con;
int n,m;
typedef pair<int,int> Problem;
Problem Prob[20][20];
inline char getc()
{
 char c;
 while(true)
 	{
 	 scanf("%c",&c);
 	 if(c!=' '&&c!='
') return c;
	 }
 return c;
}

void Init()
{
 Var.clear(); Var.resize(0);
 Con.clear(); Con.resize(0);
 scanf("%d%d",&n,&m);
 
 for(int i=1;i<=n;i++)
 	{
 	
	  for(int j=1;j<=m;j++)
 	 	 {
 	 	  char ch=getc();
		  if(ch=='*')
		  	{
		  	 Prob[i][j]=make_pair(-1,-1);	
		     continue;
			}
		  if(ch=='0')
		  	{
		  	 Variable nV;	
		  	 Prob[i][j]=make_pair(-3,(int)Var.size());
		  	 Var.push_back(nV);
		     continue;
			}
		  if(ch=='(')
		  	{
		  	 int a=0,b=0;
		  	 scanf("%d%c%d%c",&a,&ch,&b,&ch);
		  	 int c=-2,d=-2;
		  	 if(a!=0)
		  	 	{
		  	 	 Constrain nC(a);
				 c=(int)Con.size();
				 Con.push_back(nC);	
				}
			 if(b!=0)
			 	{
			 	 Constrain nC(b);
				 d=(int)Con.size();
				 Con.push_back(nC);		
				}
			 Prob[i][j]=make_pair(c,d);
		  	 continue;
			}	
	     }	
	}

 for(int i=1;i<=n;i++)
 	{
 	 for(int j=1;j<=m;j++)
 	 	{
 	 	 if(Prob[i][j].first==-1||Prob[i][j].first==-3) continue;
 	 	 
 	 	 int a=Prob[i][j].first,b=Prob[i][j].second;
 	 	 if(a!=-2)
 	 	 	{
 	 	 	 int ii=i+1;
 	 	 	 vector<int> vec;
 	 	 	 while(ii<=n&&Prob[ii][j].first==-3)
 	 	 	 	{
 	 	 	 	 vec.push_back(Prob[ii][j].second);
 	 	 	 	 ii++;
				}
				
			 for(int k=0;k<vec.size();k++)
			 	{
			 	 Var[vec[k]].Col=a;
			 	 Con[a].Scop.push_back(vec[k]);
				}
			}
		 if(b!=-2)
		 	{
		 	 int jj=j+1;
 	 	 	 vector<int> vec;
 	 	 	 while(jj<=m&&Prob[i][jj].first==-3)
 	 	 	 	{
 	 	 	 	 vec.push_back(Prob[i][jj].second);
 	 	 	 	 jj++;
				}
				
			 for(int k=0;k<vec.size();k++)
			 	{
			 	 Var[vec[k]].Row=b;
			 	 Con[b].Scop.push_back(vec[k]);
				}	
			}	
		}
	}

}

bool Support(int seted,Constrain & C)
{
 if(C.Goal<=0)return false;
 bool ret=false;
 int loc=-1,min=11;
 for(int i=0;i<C.Scop.size()&&min>2;i++)
 	{
 	 int nv=C.Scop[i];
	 if(Var[nv].Value!=0)continue;
	 if(loc==-1||Var[nv].dsize<min){loc=nv;min=Var[nv].dsize;break;}	
	}	
 if(loc==-1)return false;
 if(seted==(int)C.Scop.size())
 	{
 	 if(C.Goal<=9&&(!C.Used[C.Goal])&&Var[loc].Domain[C.Goal])return true;
 	 	else return false;
	 }
 
 for(int v=9;v>=1&&!ret;v--)
 	{
 	 if(!Var[loc].Domain[v]||v>=C.Goal||C.Used[v])continue;
	 Var[loc].Value=v;
	 C.Goal-=v;
	 C.Used[v]=true;
	 ret=Support(seted+1,C);
	 
	 Var[loc].Value=0;
	 C.Goal+=v;
	 C.Used[v]=false;
	}
 return ret;
}

bool cmp(int a,int b)
{
 return Var[a].dsize<Var[b].dsize;
}
bool GAC_Enforce(queue<int> & P,vector<pair<int,int> > & Restore)
/*
 This implementation has refered the pseudo_code for GAC in the Course Slide week8.pdf.
 Other than that, there should be no such thing like plagiarize.
 ╮(╯_╰)╭  
*/ 


{
 bool inq[1000];
 memset(inq,false,sizeof(inq));
 queue<int> Q;
 while(!P.empty())
 	{
 	 int Fr=P.front();P.pop();
 	 inq[Fr]=true;
 	 Q.push(Fr);
	}
	
 while(!Q.empty())
 	{
 	 int Fr=Q.front();Q.pop();
 	 inq[Fr]=false;
 	 sort(&Con[Fr].Scop[0],&Con[Fr].Scop[0]+(int)Con[Fr].Scop.size(),cmp);//MRV
	 for(int i=0;i<Con[Fr].Scop.size();i++)
	 	{
	 	 int nv=Con[Fr].Scop[i];
	 	 if(Var[nv].dsize<=0)return false;
	 	 for(int v=9;v>=1;v--)
	 	 	{
	 	 	 if(!Var[nv].Domain[v]||Con[Fr].Used[v])continue;
			 Var[nv].Value=v;
			 Con[Fr].Goal-=v;
			 Con[Fr].Used[v]=true;
			 if(!Support(2,Con[Fr]))
			 	{
			 	 Var[nv].Domain[v]=false;
			 	 Var[nv].dsize--;
			 	 Restore.push_back(make_pair(nv,v));
			 	 if(Var[nv].dsize==0)
			 	 	{
			 	 	 while(!Q.empty())Q.pop();
					 Var[nv].Value=0;
					 Con[Fr].Goal+=v; 
					 Con[Fr].Used[v]=false;
					 return false; 	
					}
					else
						{
							int a=Var[nv].Col,b=Var[nv].Row;
							if(a!=-1&&(!inq[a])){inq[a]=true;Q.push(a);}
							if(b!=-1&&(!inq[b])){inq[b]=true;Q.push(b);}
						}
				}
			 
			 Var[nv].Value=0;
			 Con[Fr].Goal+=v;
			 Con[Fr].Used[v]=false;
			}
		}	
	}
 return true;
}

void Reimburse(vector<pair<int,int> >& Re)
{
 for(int i=0;i<Re.size();i++)
 	{
 	 Var[Re[i].first].Domain[Re[i].second]=true;
	 Var[Re[i].first].dsize++;	
	}
 return ;
}
bool Set()
{
 bool ret=false;
 int loc=-1,min=11;
 for(int i=0;i<Var.size()&&min>2;i++)
 	{
 	 if(Var[i].dsize==1)continue;
 	 if(Var[i].dsize==0)return false;
 	 if(loc==-1||Var[i].dsize<min){loc=i;min=Var[i].dsize;}
	}
 if(loc==-1)return true;
 
 
 for(int v=9;v>=1&&!ret;v--)
 	{
 	 if(!Var[loc].Domain[v])continue;
 	 vector<pair<int,int> > Re;Re.resize(0);
 	 for(int vv=9;vv>=1;vv--)
 	 	{
 	 	 if(vv==v||(!Var[loc].Domain[vv]))continue;
 	 	 Var[loc].Domain[vv]=false;
 	 	 Var[loc].dsize--;
 	 	 Re.push_back(make_pair(loc,vv));

		}
	 queue<int> Q; while(!Q.empty())Q.pop();
	 int a=Var[loc].Col,b=Var[loc].Row;
	 if(a!=-1)Q.push(a);if(b!=-1)Q.push(b);
	 if(GAC_Enforce(Q,Re))
	 	{
	 	 ret=Set();	
	 	 if(ret)return true;
		}
	 Reimburse(Re);
	}
 return ret;
}

bool Solve()
{
 /*queue<int>Q;
 for(int i=0;i<Con.size();i++)
     Q.push(i);
 vector<pair<int,int> > V;
 GAC_Enforce(Q,V);   
  initiate GAC not necessary*/ 
 if(!Set())return false;
 for(int i=0;i<Var.size();i++)
 	{
 	 for(int v=9;v>=1;v--)
	  	{
	  	 if(Var[i].Domain[v]){Var[i].Value=v;break;}	
		}	
	}
 return true;
}


void spa(int x)
{
 for(int i=0;i<x;i++)
 	printf(" ");
}
void Print(bool flg)
{
 if(!flg)printf("%dX%d
Input:
",n,m);
 	else printf("

Solution:
");
  int ns=6;
 for(int i=1;i<=n;i++)
 {
    ns=6;
 	for(int j=1;j<=m;j++)
       {
        if(Prob[i][j].first==-3)
			{
			 spa(ns);printf("%d",Var[Prob[i][j].second].Value);	
			 ns=6;
			 continue;
			}	
		if(Prob[i][j].first==-1)
			{
			 spa(ns);printf("*");	
			 ns=6;
			 continue;
			}	
		int nr=6,a=0,b=0;
		if(Prob[i][j].first!=-2&&(a=Con[Prob[i][j].first].Goal)>=10)ns-=3;
			else ns-=2;
		if(Prob[i][j].second!=-2&&(b=Con[Prob[i][j].second].Goal)>=10)nr-=3;
			else nr-=2;
		spa(ns);printf("(%d,%d)",a,b);
		ns=nr;
	   }
	 printf("
");
 }
}
int main()
{
 for(int i=0;i<=5;i++)
 	{
	  char a[]="test5.txt";
	  char b[]="text5ans.txt";
	  a[4]=i+'0';
	  b[4]=a[4];
// 	  printf("

%s",b);
 	  freopen(a,"r",stdin);
	  freopen(b,"w",stdout); 
 	  Init();
 	  Print(0);
      if(Solve()){printf("Exists one solution
");Print(1);}
 	       else printf("No solution found
");
	}
 return 0;
}


/*
test0.txt
9 8
   *   *   *(20,0) (7,0) *   *   *
   *   *(21,4) 0     0 (8,0) *   *
   * (0,21)0   0     0   0(27,0) *
   *(12,11)0   0   (0,15)0   0 (16,0)
 (0,16)0   0   *     * (0,8) 0   0
 (0,8) 0   0(15,0)   *(20,16)0   0
   * (0,11)0   0   (9,8) 0   0   *
   *   * (0,20)0     0   0   0   *
   *   *   * (0,17)  0   0   *   *  
 
test1.txt

4 4
   *   (23,0)(21,0) (7,0) 
 (0,20)   0     0     0 
 (0,19)   0     0     0
 (0,12)   0     0     0
test2.txt

5 5
   *(16,0) (7,0) *   *
 (0,9) 0     0(24,0) *
 (0,20)0     0   0 (4,0)
   * (0,12)  0   0   0
   *   *   (0,10)0   0 
test3.txt

9 8
     *  (16,0) (6,0)   *     *   (8,0)(29,0)   *
   (0,13)  0     0  (15,0)(16,13)  0     0     *
   (0,28)  0     0     0     0     0     0  (11,0)
     *     *  (30,15)  0     0   (0,3)   0     0
     *  (16,8)   0     0     *  (22,14)  0     0
   (0,14)  0     0     *   (9,17)  0     0     *
   (0,13)  0     0   (5,10)  0     0  (12,0) (8,0)
     *   (0,32)  0     0     0     0     0     0
     *   (0,11)  0     0     *   (0,12)  0     0

test4.txt

13 13
      *   (16,0)  (7,0)    *   (16,0) (17,0)    *      *   (10,0) (16,0)    *      *      *   
    (0,9)    0      0    (0,10)   0      0    (3,0)  (0,9)    0      0      *      *      *   
    (0,10)   0      0   (16,12)   0      0      0    (3,10)   0      0      *      *      *
      *    (0,17)   0      0      0    (0,6)    0      0      0   (16,0)    *      *      *         
      *      *    (0,12)   0      0   (17,0)  (6,14)   0      0      0    (6,0)    *      *
      *      *    (3,0)  (6,13)   0      0      0    (7,0)  (0,10)   0      0   (16,0)    *
      *    (0,4)    0      0    (0,14)   0      0      0   (16,0)  (0,10)   0      0      *
      *    (0,3)    0      0   (16,0)  (0,12)   0      0      0   (35,9)    0      0      *
      *      *    (0,9)    0      0   (10,0) (17,19)   0      0      0   (16,0)    *      *
      *      *      *    (0,21)   0      0      0   (16,0)  (0,14)   0      0   (24,0)    *
      *      *      *      *   (16,17)   0      0      0    (4,24)   0      0      0    (3,0)
      *      *      *    (0,10)   0      0    (0,19)   0      0      0    (0,11)   0      0
      *      *      *    (0,11)   0      0      *    (0,7)    0      0    (0,8)    0      0
test5.txt

15 15
      *      *      *   (35,0) (17,0)  (6,0)    *   (17,0)  (6,0)    *   (16,0)  (6,0)    *      *      *
      *      *    (0,15)   0      0      0    (0,12)   0      0   (28,9)    0      0      *      *      *
      *      *    (4,18)   0      0      0   (16,26)   0      0      0      0      0    (4,0)    *      *
      *    (0,9)    0      0    (0,10)   0      0    (4,4)    0      0    (3,4)    0      0   (39,0)    *
      *    (0,12)   0      0   (16,0)  (0,12)   0      0   (17,5)    0      0    (0,9)    0      0    (3,0)
      *    (4,0) (22,12)   0      0   (24,0)  (0,19)   0      0      0      0      *   (16,5)    0      0
    (0,10)   0      0    (0,17)   0      0   (41,0)  (0,10)   0      0   (23,0)  (0,18)   0      0      0
    (0,4)    0      0   (17,0)  (0,9)    0      0      *    (0,7)    0      0    (0,14)   0      0   (16,0)
      *    (4,13)   0      0    (0,17)   0      0    (4,0)  (0,14)   0      0    (3,0)  (0,16)   0      0
    (0,13)   0      0      0      *   (17,5)    0      0   (16,0)  (0,9)    0      0   (16,15)   0      0
    (0,3)    0      0   (16,0)  (0,25)   0      0      0      0    (3,0)  (0,6)    0      0   (16,0)    *
      *    (0,11)   0      0   (24,15)   0      0    (7,11)   0      0    (6,0)  (0,10)   0      0      *
      *      *    (0,16)   0      0    (4,9)    0      0   (16,3)    0      0   (16,11)   0      0      *
      *      *      *    (0,27)   0      0      0      0      0    (0,13)   0      0      0      *      *
      *      *      *    (0,12)   0      0    (0,10)   0      0    (0,14)   0      0      0      *      *
*/