技巧性很强的一道二分优化题
题意很简单 给定n个三元组,和三个维度的上限,问存在多少三元组,使得对于给定的n个三元组中的每一个,必有两个维度严格小于。
首先我们根据一个维度(c维)对n个三元组排序,然后枚举答案在这个维度的取值。
此时序列被分成了两个部分,前半部分 满足所有c大于等于i 后半部分满足所有c严格小于i(即已有一个维度小于)
通过累计,我们知道此时前半部a维的最大值ma和b维的最大值mb.
显然可能存在的三元组答案,必然首先满足a维和b维严格大于ma和mb.
后面我们考虑对于后半部分,即c严格小于i的部分,可能存在某些三元组 ai和bi非常大,以致于上边的答案不合法。
这时,我们想知道,对于ai大于ma的那些三元组,其对应的bi能有多大?
我们可以用一个mx数组提前统计这个值。
那么,当ai大到一定程度,其对应的bi就不可能大于mb了 我们可以二分找到这个边界ret
对于ma到ret这个范围的值,我们让第一维取其中的某个值,对应的第二维b有多少种可能呢?
所有ai大于当前值的对应的bi的最大值。 因为若ai小于当前值,就不需要保证第二维大于bi了。。
具体看代码吧 有点难以描述。
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define maxn 500005
#define ll long long
using namespace std;
ll sum[maxn],mx[maxn];
ll n,p,q,r;
ll ans;
struct note{
int a,b,c;
}a[maxn];
bool cmp(note i,note j){
return i.c>j.c;
}
int main(){
scanf("%I64d%I64d%I64d%I64d",&n,&p,&q,&r);
fo(i,1,n) scanf("%d%d%d",&a[i].a,&a[i].b,&a[i].c);
fo(i,1,n) mx[a[i].a]=max(mx[a[i].a],(ll)a[i].b+1);
fd(i,p,1) mx[i]=max(mx[i+1],mx[i]);//可能存在的最大b值
fo(i,1,p) sum[i]=sum[i-1]+(q-mx[i])+1;
ll ma=1,mb=1;
sort(a+1,a+n+1,cmp);
int wz=1;
fd(i,r,1) {
while (wz<=n && a[wz].c==i) {
ma=max(ma,a[wz].a+1ll);
mb=max(mb,a[wz].b+1ll);
wz++;
}
if (ma>p || mb>q) break;
int x=ma,y=p,ret=ma-1;
while (x<=y) {
int mid=(x+y) >> 1;
if (mx[mid]>=mb) {
x=mid+1;
ret=mid;
}
else y=mid-1;
}
ans+=sum[ret]-sum[ma-1]+1ll*(p-ret)*(q-mb+1);
}
cout<<ans;
return 0;
}
题意非常简单 不必赘述
整个过程其实是一个满二叉树的层次遍历,问我们遍历到的第k个元素是哪一个。对数复杂度
先给出遍历的二叉树 其规律非常明显
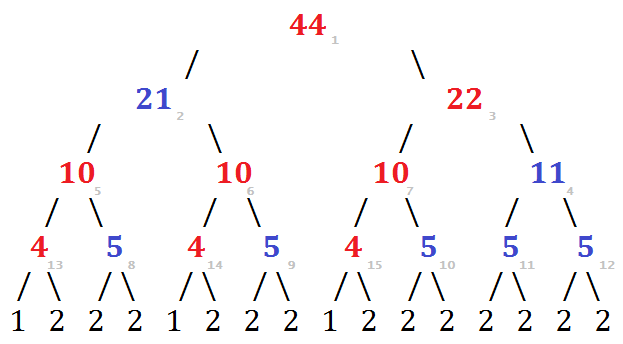
我们可以在对数时间内快速寻找到第k个节点,但是我们的空间不足以储存所有的节点信息。
那么怎么办呢? 我们首先判断这个节点在哪一个层次,即它与邻居的最短距离是多少。
然后我们再二分判断这个节点在整个序列中的位置,我们可以快速判断一个区间产生能够产生多少个距离为len的子节点。与k比较即可。
于是总的复杂度是二分套二分 即O(lognlogn)
这道题让我们深入理解了满二叉树的层次遍历
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,k;
int main(){
scanf("%lld%lld",&n,&k);
if(k==1)return printf("1"),0;
if(k==2)return printf("%lld",n),0;
n-=2,k-=3;
map<ll,ll>f,g,nxt;
g[n]=1;
while(g.size()){
nxt.clear();
for(auto s:g)if(s.first)
f[-((s.first-1)>>1)]+=s.second,
nxt[(s.first)>>1]+=s.second,
nxt[(s.first-1)>>1]+=s.second;
g=nxt;
}
for(auto s:f){
//printf("[%d]",s.first);
if(s.second>k){//确定在哪一层
ll l=1,r=n,len=-s.first;
// printf("[%d]",len);
while(true){
if(((r-l)>>1)==len&&k==0)
return printf("%lld",((r-l)>>1)+1+l),0;
map<ll,ll>A,B,C;
ll mid=l+r>>1;
A[mid-l]=1;
B[(r-l)>>1]=1;
while(A.size()){
C.clear();
for(auto qs:A)if(qs.first)
B[(qs.first-1)>>1]+=qs.second,//
C[(qs.first)>>1]+=qs.second,
C[(qs.first-1)>>1]+=qs.second;
A=C;
}
// printf("[%d]",B[len]);
if(B[len]>k)r=mid-1;
else l=mid+1,k-=B[len];
}
} else k-=s.second;
}
}