此文转载:
http://www.cnblogs.com/skywang12345/p/3577360.html
AVL树是一棵特殊的高度平衡的二叉树,每个节点的两棵子树高度最大差为1。所以在每次的删除或者是插入的过程之后都要判断此时是否是一颗AVL树,AVL树不平衡的调整最关键,大概分为四种不同的不平衡的状态。处理四种不平衡状态四个调整函数(LL,RR,LR,Rl)即可;


(1) LL:LeftLeft,也称为"左左"。插入或删除一个节点后,根节点的左子树的左子树还有非空子节点,导致"根的左子树的高度"比"根的右子树的高度"大2,导致AVL树失去了平衡。
例如,在上面LL情况中,由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点",而"根节点(8)的右子树(12)没有子节点";导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
(2) LR:LeftRight,也称为"左右"。插入或删除一个节点后,根节点的左子树的右子树还有非空子节点,导致"根的左子树的高度"比"根的右子树的高度"大2,导致AVL树失去了平衡。
例如,在上面LR情况中,由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点",而"根节点(8)的右子树(12)没有子节点";导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
(3) RL:RightLeft,称为"右左"。插入或删除一个节点后,根节点的右子树的左子树还有非空子节点,导致"根的右子树的高度"比"根的左子树的高度"大2,导致AVL树失去了平衡。
例如,在上面RL情况中,由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点",而"根节点(8)的左子树(4)没有子节点";导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
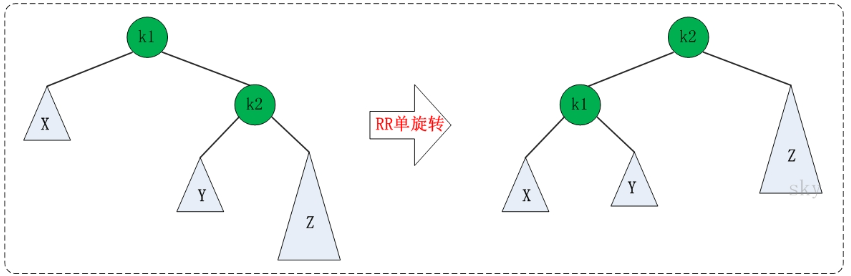
(4) RR:RightRight,称为"右右"。插入或删除一个节点后,根节点的右子树的右子树还有非空子节点,导致"根的右子树的高度"比"根的左子树的高度"大2,导致AVL树失去了平衡。
例如,在上面RR情况中,由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点",而"根节点(8)的左子树(4)没有子节点";导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
LL旋转:

RR旋转:
LR旋转:

RL旋转:

因为博客园中我还不知道如何转载原文,所以只能以这种方式;
第八次作业:
下面是我自己根据原文代码做题写的C语言的代码(没有全A,不知为何)
2、题目链接(多次删除操作多次寻找树中的最大最小值):
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<malloc.h>
using namespace std;
int n;
int nodes[100005];
int dep[100005];
int depth = 0;
typedef struct AVL_Node
{
int data;
int height;
AVL_Node* left;
AVL_Node* right;
}Node, *AVLTree;
int MAX(int a, int b)
{
return a < b ? b : a;
}
int Height(AVLTree tree) //返回该节点树的高度;
{
return tree == NULL ? 0 : tree->height;
}
Node* create_node(int data, Node* left, Node* right)
{
Node* p;
if ((p = (Node*)malloc(sizeof(Node))) == NULL)
return NULL;
p->data = data;
p->height = 0;
p->left = left;
p->right = right;
return p;
}
Node* L_L(AVLTree tree)
{
AVLTree tmp;
tmp = tree->left;
tree->left = tmp->right;
tmp->right = tree;
tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
tmp->height = MAX(Height(tmp->left), tree->height) + 1;
return tmp;
}
Node* R_R(AVLTree tree)
{
AVLTree tmp;
tmp = tree->right;
tree->right = tmp->left;
tmp->left = tree;
tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
tmp->height = MAX(Height(tmp->right), tree->height) + 1;
return tmp;
}
Node* L_R(AVLTree tree)
{
tree->left = R_R(tree->left);
return L_L(tree);
}
Node* R_L(AVLTree tree)
{
tree->right = L_L(tree->right);
return R_R(tree);
}
Node* maximum(Node* tree)
{
if (tree == NULL)return NULL;
while(tree->right!=NULL)
{
tree = tree->right;
}
return tree;
}
Node* minimun(Node* tree)
{
if (tree == NULL)return NULL;
while(tree->left!=NULL)
{
tree = tree->left;
}
return tree;
}
Node* insert(AVLTree tree, int data)
{
if (tree == NULL)
{
tree = create_node(data, NULL, NULL);
if (tree == NULL)
return NULL;
}
else if (data < tree->data) //根据AVL树的性质应该插入到左子树中
{
tree->left = insert(tree->left, data);
if (Height(tree->left) - Height(tree->right) == 2) //插入后树如果不平衡,则应进行调节;
{
if (data < tree->left->data)
tree = L_L(tree);
else
tree = L_R(tree);
}
}
else if (data > tree->data)
{
tree->right = insert(tree->right, data);
if (Height(tree->right) - Height(tree->left) == 2)
{
if (data < tree->right->data)
tree = R_L(tree);
else
tree = R_R(tree);
}
}
tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
return tree;
}
Node* Delete(AVLTree tree,Node* dele)
{
if (tree == NULL || dele == NULL)return NULL; //根为空或者没有要删除的节点,直接返回NULL;
if (dele->data < tree->data) //删除节点在左子树中;
{
tree->left = Delete(tree->left, dele);
if (Height(tree->right) - Height(tree->left) == 2)//失去平衡之后要重新调整;
{
Node* tmp = tree->right;
if (Height(tmp->left) > Height(tmp->right))
tree = R_L(tree);
else
tree = R_R(tree);
}
}
else if (dele->data > tree->data) //删除节点在右子树中;
{
tree->right = Delete(tree->right, dele);
if (Height(tree->left) - Height(tree->right) == 2)//失去平衡之后要重新调整;
{
Node* tmp = tree->left;
if (Height(tmp->right) > Height(tmp->left))
tree = L_R(tree);
else
tree = L_L(tree);
}
}
else
{
if ((tree->left != NULL) && (tree->right != NULL))
{
if (Height(tree->left) > Height(tree->right))
{
// 如果tree的左子树比右子树高;
// 则(01)找出tree的左子树中的最大节点
// (02)将该最大节点的值赋值给tree。
// (03)删除该最大节点。
// 这类似于用"tree的左子树中最大节点"做"tree"的替身;
// 采用这种方式的好处是:删除"tree的左子树中最大节点"之后,AVL树仍然是平衡的。
Node* max = maximum(tree->left);
tree->data = max->data;
tree->left = Delete(tree->left, max);
}
else
{
// 如果tree的左子树不比右子树高(即它们相等,或右子树比左子树高1)
// 则(01)找出tree的右子树中的最小节点
// (02)将该最小节点的值赋值给tree。
// (03)删除该最小节点。
// 这类似于用"tree的右子树中最小节点"做"tree"的替身;
// 采用这种方式的好处是:删除"tree的右子树中最小节点"之后,AVL树仍然是平衡的。
Node* min = minimun(tree->right);
tree->data = min->data;
tree->right = Delete(tree->right, min);
}
}
else
{
Node* tmp = tree;
tree = (tree->left != NULL) ? tree->left : tree->right;
free(tmp);
}
}
return tree;
}
Node* mininode(AVLTree tree,AVLTree tmproot) //寻找最小键值的节点;
{
int depth = 1;
if (tree == NULL)return NULL;
while (tree->left != NULL)
{
tree = tree->left; depth++;
}
cout << tree->data << " " << depth << endl;
return Delete(tmproot, tree);
}
Node* maxnode(AVLTree tree,AVLTree tmproot) //寻找最大键值的节点;
{
int depth = 1;
if (tree == NULL)return NULL;
while (tree->right != NULL)
{
tree = tree->right; depth++;
}
cout << tree->data << " " << depth << endl;
return Delete(tmproot, tree);
}
int main()
{
int i, tmp1, tmp2;
AVLTree root = NULL;
cin >> n;
for (i = 1; i <= n; i++)
{
cin >> nodes[i];
root = insert(root, nodes[i]);
}
int m, j = 0;
cin >> m;
for (i = 1; i <= m; i++)
{
cin >> tmp1;
if (tmp1 == 1)
{
if (j >= n) { cout << "-1
"; continue; }
root = maxnode(root, root); j++;
}
else if (tmp1 == 2)
{
if (j >= n) { cout << "-1
"; continue; }
root = mininode(root, root); j++;
}
else if (tmp1 == 3)
{
cin >> tmp2;
insert(root, tmp2);
j--;
}
}
return 0;
}
1、题目链接(找出每个节点的深度即层次)
代码:
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<malloc.h>
using namespace std;
int n;
int nodes[100005];
int dep[100005];
int depth = 0;
typedef struct AVL_Node
{
int data;
int height;
AVL_Node* left;
AVL_Node* right;
}Node, *AVLTree;
int MAX(int a, int b)
{
return a < b ? b : a;
}
int Height(AVLTree tree)
{
return tree == NULL ? 0 : tree->height;
}
Node* create_node(int data, Node* left, Node* right)
{
Node* p;
if ((p = (Node*)malloc(sizeof(Node))) == NULL)
return NULL;
p->data = data;
p->height = 0;
p->left = left;
p->right = right;
return p;
}
Node* L_L(AVLTree tree)
{
AVLTree tmp;
tmp = tree->left;
tree->left = tmp->right;
tmp->right = tree;
tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
tmp->height = MAX(Height(tmp->left), tree->height) + 1;
return tmp;
}
Node* R_R(AVLTree tree)
{
AVLTree tmp;
tmp = tree->right;
tree->right = tmp->left;
tmp->left = tree;
tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
tmp->height = MAX(Height(tmp->right), tree->height) + 1;
return tmp;
}
Node* L_R(AVLTree tree)
{
/*AVLTree tmp1, tmp2;
tmp2 = tree->left;
tmp1 = tmp2->right;
tmp2->right = tmp1->left;
tmp1->left = tmp2;
tree->left = tmp1;*/
tree->left = R_R(tree->left);
return L_L(tree);
}
Node* R_L(AVLTree tree)
{
tree->right = L_L(tree->right);
return R_R(tree);
}
Node* insert(AVLTree tree, int data)
{
if (tree == NULL)
{
tree = create_node(data, NULL, NULL);
if (tree == NULL)
return NULL;
}
else if (data < tree->data) //根据AVL树的性质应该插入到左子树中
{
tree->left = insert(tree->left, data);
if (Height(tree->left) - Height(tree->right) == 2)
{
if (data < tree->left->data)
tree = L_L(tree);
else
tree = L_R(tree);
}
}
else if (data > tree->data)
{
tree->right = insert(tree->right, data);
if (Height(tree->right) - Height(tree->left) == 2)
{
if (data < tree->right->data)
tree = R_L(tree);
else
tree = R_R(tree);
}
}
tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
return tree;
}
void mid_Tree(AVLTree tree) //中序遍历树,即从小到大遍历
{
if (tree != NULL)
{
depth++; //每向下走一步就加一
mid_Tree(tree->left);
dep[tree->data] = depth;
mid_Tree(tree->right);
depth--; //往上回走一步减一(回溯过程)
}
}
int main()
{
int i, tmp;
AVLTree root = NULL;
cin >> n;
for (i = 1; i <= n; i++)
{
cin >> nodes[i];
root = insert(root, nodes[i]);
}
mid_Tree(root);
for (i = 1; i <= n; i++)
printf("%d%c", dep[nodes[i]], i != n ? ' ' : '
');
return 0;
}
其次我认为最主要是给定一个数列之后,会将其AVL树画出来;
具体可以参见博客:http://www.cnblogs.com/skywang12345/p/3577360.html