Xor-sequences CodeForces

Xor-sequences CodeForces - 691E

题意：在有n个数的数列中选k个数（可以重复选，可以不按顺序）形成一个数列，使得任意相邻两个数异或的结果转换成二进制后其中1的个数是三的倍数。求可能形成的不同数列个数（只要选出的数列中，任意两个元素在原序列中的位置不同，就算作不同的序列，比如在原数列[1,1]中选1个，那么第一个1和第二个1要分开算）。

方法：

很容易列出dp方程：

dp[k][i]表示取了k个，最后一个在第i位。a[i][j]表示i和j异或结果转换成二进制后1的个数是否是3的倍数，1表示是，0表示否。

$dp[k][i]=dp[k-1][1]*a[1][i]+...dp[k-1][n]*a[n][i]$

注意，不是$dp[k][i]=dp[k-1][1]*a[1][i]+...+dp[k-1][i-1]*a[i-1][i]$（这道题是可以重复、不按顺序选的，这么写就是不重复、按顺序）

那么，这样的算法复杂度就是O(nk)，太慢了，需要优化。

从小数据开始：

n=3时：

dp[1][1]=1
dp[1][2]=1
dp[1][3]=1

dp[2][1]=dp[1][1]*a[1][1]+dp[1][2]*a[2][1]+dp[1][3]*a[3][1]
dp[2][2]=dp[1][1]*a[1][2]+dp[1][2]*a[2][2]+dp[1][3]*a[3][2]
dp[2][3]=dp[1][1]*a[1][3]+dp[1][2]*a[2][3]+dp[1][3]*a[3][3]

dp[3][1]=dp[2][1]*a[1][1]+dp[2][2]*a[2][1]+dp[2][3]*a[3][1]
dp[3][2]=dp[2][1]*a[1][2]+dp[2][2]*a[2][2]+dp[2][3]*a[3][2]
dp[3][3]=dp[2][1]*a[1][3]+dp[2][2]*a[2][3]+dp[2][3]*a[3][3]

很容易可以发现：
矩阵1
dp[1][1] dp[1][2] dp[1][3]
矩阵2
 a[1][1]  a[1][2]  a[1][3]
 a[2][1]  a[2][2]  a[2][3]
 a[3][1]  a[3][2]  a[3][3]
矩阵1*矩阵2
dp[2][1] dp[2][2] dp[2][3]

更大的数据以此类推，因此很容易想到用矩阵快速幂优化。

而要求dp[k][]，就要由dp[1][]乘k-1次矩阵2，可以改为算出来矩阵2的k-1次幂放入矩阵3，再将dp[1][]乘上矩阵3，得到的就是dp[k][]。最终答案就是dp[k][1]+..+dp[k][n]。

所以说...这个矩阵快速幂的题..居然不用自己去构造转移矩阵??

另外：

__builtin_popcountll：参照__builtin_popcount，那个是针对long整型的，这个是针对long long的

还有手动写的

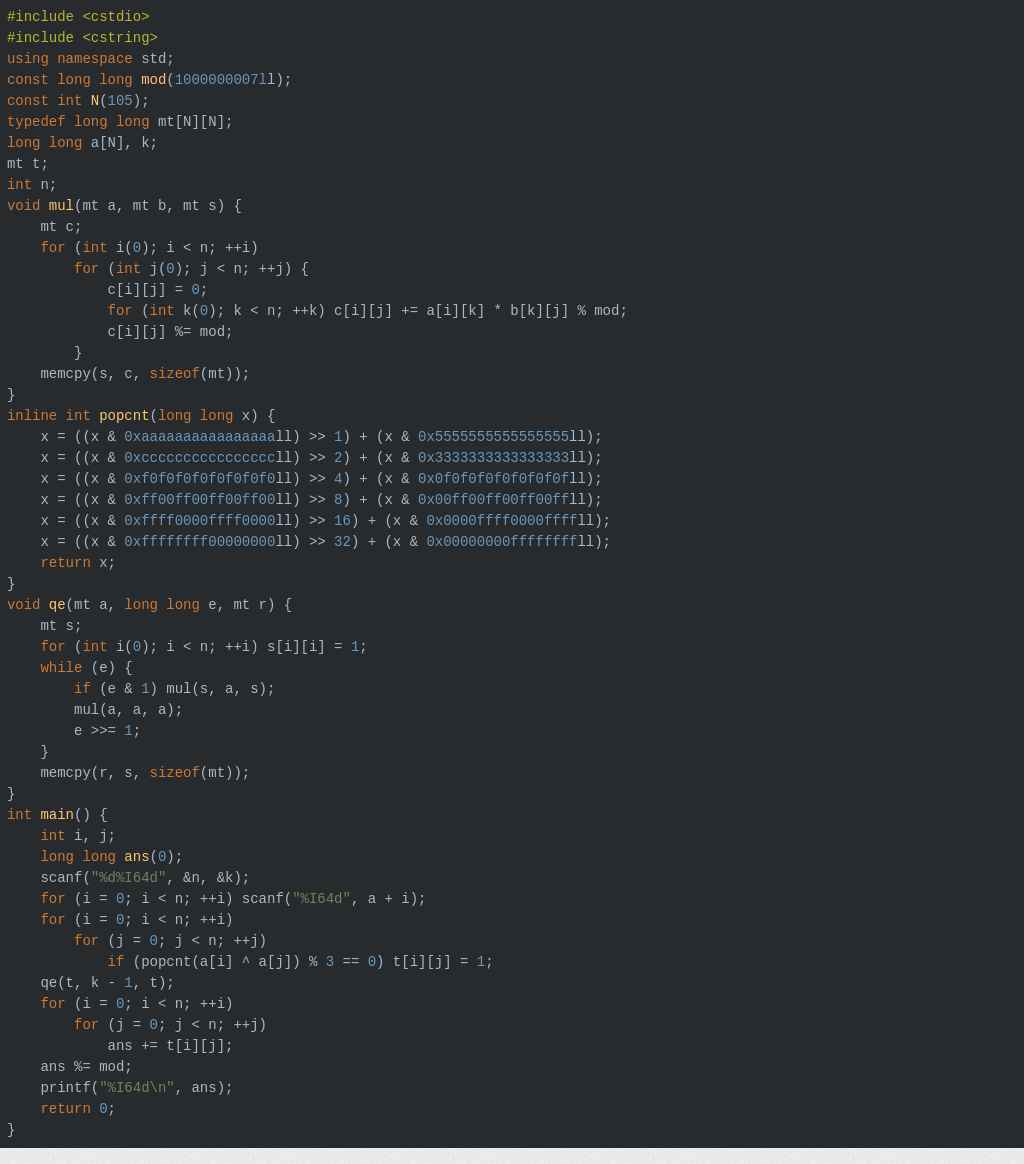
#include<cstdio>
#include<cstring>
#define md 1000000007
typedef long long LL;
LL n,k,anss;
LL a[101];
struct Mat
{
    LL data[101][101],x,y;
    Mat()
    {
        memset(data,0,sizeof(data));
        x=y=0;
    }
    Mat operator*(const Mat& b)
    {
        Mat temp;
        LL i,j,k;
        for(i=1;i<=x;i++)
            for(j=1;j<=b.y;j++)
                for(k=1;k<=y;k++)
                    temp.data[i][j]=(data[i][k]*b.data[k][j]+temp.data[i][j])%md;
        temp.x=x;
        temp.y=b.y;
        return temp;
    }
    Mat& operator*=(const Mat& b)
    {
        return (*this)=(*this)*b;
    }
    Mat& operator=(const Mat& b)
    {
        memcpy(data,b.data,sizeof(data));
        x=b.x;
        y=b.y;
        return *this;
    }
}ma,o,bbb,ccc;
Mat pow(const Mat& a,LL b)
{
    Mat ans=o;
    if(b==0)    return ans;
    Mat base=a;
    while(b!=0)
    {
        if(b&1!=0)    ans*=base;
        base*=base;
        b>>=1;
    }
    return ans;
}
int main()
{
    LL i,j;
    scanf("%I64d%I64d",&n,&k);
    for(i=1;i<=n;i++)
        scanf("%I64d",&a[i]);
    ma.x=ma.y=n;
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            ma.data[i][j]=(__builtin_popcountll(a[i]^a[j])%3==0);
    o.x=o.y=n;
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            o.data[i][j]=(i==j);
    bbb=pow(ma,k-1);
    ccc.x=1;ccc.y=n;
    for(i=1;i<=n;i++)
        ccc.data[1][i]=1;
    ccc*=bbb;
    for(i=1;i<=n;i++)
        anss=(anss+ccc.data[1][i])%md;
    printf("%I64d",anss);
    return 0;
}