堆:
①堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
·堆中某个节点的值总是不大于或不小于其父节点的值;
·堆总是一棵完全二叉树。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
②堆是在程序运行时,而不是在程序编译时,申请某个大小的内存空间。即动态分配内存,对其访问和对一般内存的访问没有区别。
③堆是应用程序在运行的时候请求操作系统分配给自己内存,一般是申请/给予的过程。
④堆是指程序运行时申请的动态内存,而栈只是指一种使用堆的方法(即先进后出)。
堆的应用:
#堆排序
def sift(li, left, right):
i = left
j = 2 * i + 1
tmp = li[left]
while j <= right:
if j+1 <= right and li[j] < li[j+1]:
j = j + 1
if tmp < li[j]:
li[i] = li[j]
i = j
j = 2 * i + 1
else:
break
li[i] = tmp
def heap_sort(li):
n = len(li)
for i in range(n//2-1, -1, -1): #建立堆
sift(li, i, n-1)
for i in range(n-1, -1, -1): #挨个出数
li[0], li[i] = li[i],li[0]
sift(li, 0, i-1)
li = [6,8,1,9,3,0,7,2,4,5]
heap_sort(li)
print(li)
栈:
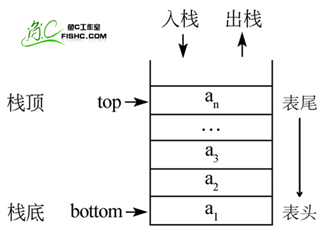
①栈(stack)又名堆栈,一个数据集合,可以理解为只能在一端进行插入或删除操作的列表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶,相对地,把另一端称为栈底。
②栈就是一个桶,后放进去的先拿出来,它下面本来有的东西要等它出来之后才能出来(先进后出)
③栈(Stack)是操作系统在建立某个进程时或者线程(在支持多线程的操作系统中是线程)为这个线程建立的存储区域,该区域具有FIFO的特性,在编译的时候可以指定需要的Stack的大小。
栈的基本操作:
进栈(压栈):push
出栈:pop
取栈顶:gettop
用python实现堆栈
# 后进先出
class Stack():
def __init__(self,size):
self.size=size
self.stack=[]
self.top=-1
def push(self,x):
if self.isfull():
raise exception("stack is full")
else:
self.stack.append(x)
self.top=self.top+1
def pop(self):
if self.isempty():
raise exception("stack is empty")
else:
self.top=self.top-1
self.stack.pop()
def isfull(self):
return self.top+1 == self.size
def isempty(self):
return self.top == '-1'
def showStack(self):
print(self.stack)
s=Stack(10)
for i in range(5):
s.push(i)
s.showStack()
for i in range(3):
s.pop()
s.showStack()
"""
类中有top属性,用来指示栈的存储情况,初始值为1,一旦插入一个元素,其值加1,利用top的值乐意判定栈是空还是满。
执行时先将0,1,2,3,4依次入栈,然后删除栈顶的前三个元素
"""
栈的应用——括号匹配问题
括号匹配问题:给一个字符串,其中包含小括号、中括号、大括号,求该字符串中的括号是否匹配。例如:
()()[]{} 匹配
([{()}]) 匹配
[]( 不匹配
[(]) 不匹配

def kuohao_match(exp): stack = [] di = {'(':')', '{':'}', '[':']'} for c in exp: if c in {'(','{', '['}: stack.append(c) else: if len(stack) == 0: return False top = stack.pop() if di[top] != c: return False if len(stack) > 0: return False else: return True print(kuohao_match('()[]{([]][]}()'))
栈的应用——迷宫问题

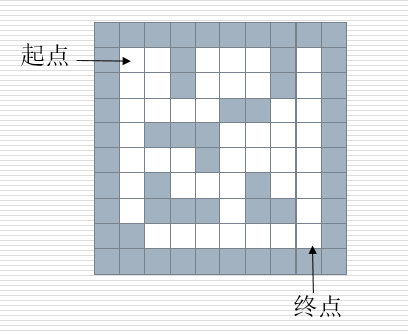

''' 解决思路 在一个迷宫节点(x,y)上,可以进行四个方向的探查:maze[x-1][y], maze[x+1][y], maze[x][y-1], maze[x][y+1] 思路:从一个节点开始,任意找下一个能走的点,当找不到能走的点时,退回上一个点寻找是否有其他方向的点。 方法:创建一个空栈,首先将入口位置进栈。当栈不空时循环:获取栈顶元素,寻找下一个可走的相邻方块,如果找不到可走的相邻方块,说明当前位置是死胡同,进行回溯(就是讲当前位置出栈,看前面的点是否还有别的出路) ''' maze = [ [1,1,1,1,1,1,1,1,1,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,0,0,1,1,0,0,1], [1,0,1,1,1,0,0,0,0,1], [1,0,0,0,1,0,0,0,0,1], [1,0,1,0,0,0,1,0,0,1], [1,0,1,1,1,0,1,1,0,1], [1,1,0,0,0,0,0,1,0,1], [1,1,1,1,1,1,1,1,1,1] ] dirs = [lambda x, y: (x + 1, y), lambda x, y: (x - 1, y), lambda x, y: (x, y - 1), lambda x, y: (x, y + 1)] def mpath(x1, y1, x2, y2): stack = [] stack.append((x1, y1)) while len(stack) > 0: curNode = stack[-1] if curNode[0] == x2 and curNode[1] == y2: #到达终点 for p in stack: print(p) return True for dir in dirs: nextNode = dir(curNode[0], curNode[1]) if maze[nextNode[0]][nextNode[1]] == 0: #找到了下一个 stack.append(nextNode) maze[nextNode[0]][nextNode[1]] = -1 # 标记为已经走过,防止死循环 break else:#四个方向都没找到 maze[curNode[0]][curNode[1]] = -1 # 死路一条,下次别走了 stack.pop() #回溯 print("没有路") return False mpath(1,1,8,8)
队列
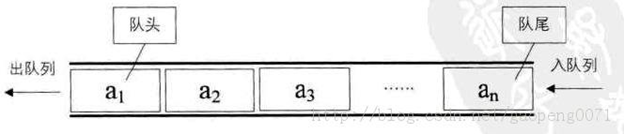
- 队列(Queue)是一个数据集合,仅允许在列表的一端进行插入,另一端进行删除。
- 进行插入的一端称为队尾(rear),插入动作称为进队或入队
- 进行删除的一端称为队头(front),删除动作称为出队
- 队列的性质:先进先出(First-in, First-out)
- 双向队列:队列的两端都允许进行进队和出队操作
使用方法:from collections import deque
创建队列:queue = deque(li)
进队:append
出队:popleft
双向队列队首进队:appendleft
双向队列队尾进队:pop
队列的实现原理




队列的实现原理:环形队列
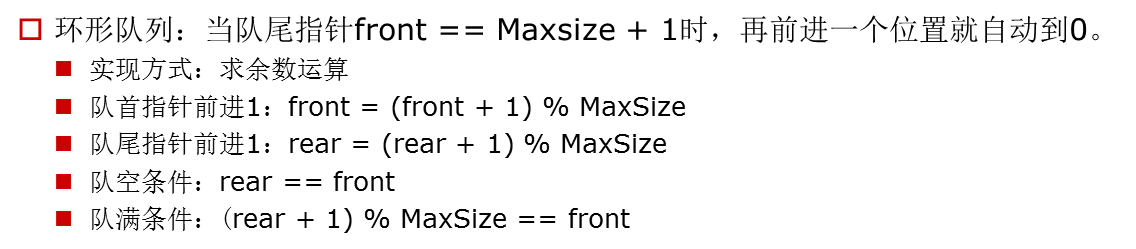
队列的应用:

''' 思路:从一个节点开始,寻找所有下面能继续走的点。继续寻找,直到找到出口。 方法:创建一个空队列,将起点位置进队。在队列不为空时循环:出队一次。如果当前位置为出口,则结束算法;否则找出当前方块的4个相邻方块中可走的方块,全部进队。 ''' from collections import deque mg = [ [1,1,1,1,1,1,1,1,1,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,0,0,1,1,0,0,1], [1,0,1,1,1,0,0,0,0,1], [1,0,0,0,1,0,0,0,0,1], [1,0,1,0,0,0,1,0,0,1], [1,0,1,1,1,0,1,1,0,1], [1,1,0,0,0,0,0,1,0,1], [1,1,1,1,1,1,1,1,1,1] ] dirs = [lambda x, y: (x + 1, y), lambda x, y: (x - 1, y), lambda x, y: (x, y - 1), lambda x, y: (x, y + 1)] def print_p(path): curNode = path[-1] realpath = [] print('迷宫路径为:') while curNode[2] != -1: realpath.append(curNode[0:2]) curNode = path[curNode[2]] realpath.append(curNode[0:2]) realpath.reverse() print(realpath) def mgpath(x1, y1, x2, y2): queue = deque() path = [] queue.append((x1, y1, -1)) mg[x1][y1] = -1 while len(queue) > 0: curNode = queue.popleft() path.append(curNode) if curNode[0] == x2 and curNode[1] == y2: #到达终点 # for i,j,k in path: # print("(%s,%s) %s"%(i,j,k)) print_p(path) return True for dir in dirs: nextNode = dir(curNode[0], curNode[1]) if mg[nextNode[0]][nextNode[1]] == 0: # 找到下一个方块 queue.append((nextNode[0], nextNode[1], len(path) - 1)) mg[nextNode[0]][nextNode[1]] = -1 # 标记为已经走过 return False mgpath(1,1,8,8)
链表
链表中每一个元素都是一个对象,每个对象称为一个节点,包含有数据域key和指向下一个节点的指针next。通过各个节点之间的相互连接,最终串联成一个链表。
节点的定义:
class Node(object):
def __init__(self, item):
self.item = item
self.next = None
头节点:

链表的遍历:
#遍历链表
def traversal(head):
curNode = head #临时用指针
while cueNode is not None:
print(curNode.data)
curNode = curNode.Next

链表节点的插入和删除
插入: p.next = curNode.next curNode.next = p 删除: p = curNode.next curNode.next = curNode.next.next del p
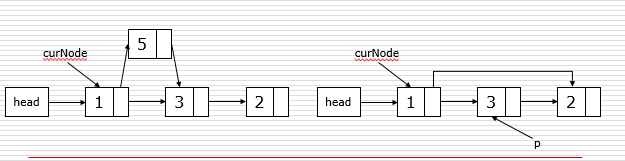
建立链表
#头插法:
def createLinkListF(li):
l = Node()
for num in li:
s = Node(num)
s.next = l.next
l.next = s
return l

#尾插法
def createLinkListR(li):
l = Node()
r = l #r指向尾节点
for num in li:
s = Node(num)
r.next = s
r = s
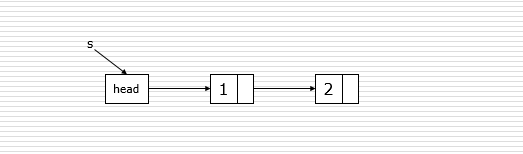
双链表
双链表中每个节点有两个指针:一个指向后面节点、一个指向前面节点。
节点定义:
class Node(object):
def __init__(self, item=None):
self.item = item
self.next = None
self.prior = None
双链表的插入和删除
#插入: p.next = curNode.next curNode.next.prior = p p.prior = curNode curNode.next = p #删除: p = curNode.next curNode.next = p.next p.next.prior = curNode del p
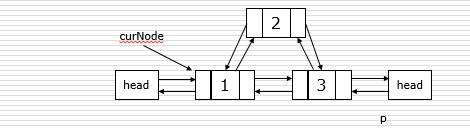
建立双链表
def createLinkListR(li):
l = Node()
r = l
for num in li:
s = Node(num)
r.next = s
s.prior = r
r = s
return l, r
栈与队列的异同
栈(Stack)和队列(Queue)是两种操作受限的线性表。
(线性表:线性表是一种线性结构,它是一个含有n≥0个结点的有限序列,同一个线性表中的数据元素数据类型相同并且满足“一对一”的逻辑关系。
“一对一”的逻辑关系指的是对于其中的结点,有且仅有一个开始结点没有前驱但有一个后继结点,有且仅有一个终端结点没有后继但有一个前驱结点,其它的结点都有且仅有一个前驱和一个后继结点。)
这种受限表现在:栈的插入和删除操作只允许在表的尾端进行(在栈中成为“栈顶”),满足“FIFO:First In Last Out”;队列只允许在表尾插入数据元素,在表头删除数据元素,满足“First In First Out”。
栈与队列的相同点:
1.都是线性结构。
2.插入操作都是限定在表尾进行。
3.都可以通过顺序结构和链式结构实现。、
4.插入与删除的时间复杂度都是O(1),在空间复杂度上两者也一样。
5.多链栈和多链队列的管理模式可以相同。
栈与队列的不同点:
1.删除数据元素的位置不同,栈的删除操作在表尾进行,队列的删除操作在表头进行。
2.应用场景不同;常见栈的应用场景包括括号问题的求解,表达式的转换和求值,函数调用和递归实现,深度优先搜索遍历等;常见的队列的应用场景包括计算机系统中各种资源的管理,消息缓冲器的管理和广度优先搜索遍历等。
3.顺序栈能够实现多栈空间共享,而顺序队列不能。
