学习笔记92—python 画横竖分界线

python画横线竖线作为分界线

在作图的时候，经常会碰到需要添加分界线的情况，那么python里面那些函数可以方便的画出水平横线或者垂直竖线呢，下面介绍两种可以方便的添加水平或者垂直直线的函数。

1.使用matplotlib.pyplot的hlines和vhlines

######导入需要模块
import numpy as np
import matplotlib.pyplot as plt
######这是蝴蝶曲线部分
df = sns.load_dataset('iris')
t = np.arange(0.0, 12*np.pi, 0.01)
x = np.sin(t)*(np.e**np.cos(t) - 2*np.cos(4*t)-np.sin(t/12)**5)
y = np.cos(t)*(np.e**np.cos(t) - 2*np.cos(4*t)-np.sin(t/12)**5)
plt.figure(figsize=(8,6))

plt.plot(x,y,color='blue',linewidth = '3')
#######这是分割线部分
plt.hlines(0, -3, 3,color="red")#横线
plt.vlines(0, -2, 3,color="red")#竖线

Python

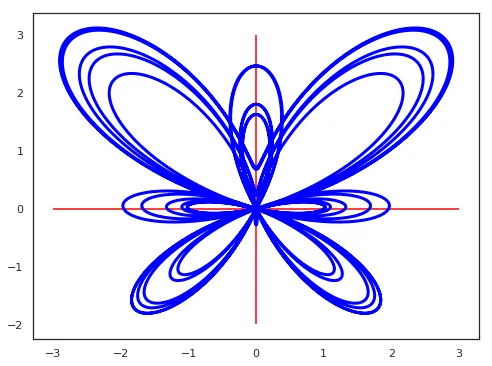
matplotlib.pyplot.hlines(y, xmin, xmax)表示横线，参数(y的值，横线开始横坐标，横线结束横坐标)

matplotlib.pyplot.vlines(y, xmin, xmax)表示竖线，参数(x的值，竖线开始纵坐标，竖线结束纵坐标)

2.使用matplotlib.pyplot的axhlines和axvhlines

######导入模块
import numpy as np
import matplotlib.pyplot as plt
######这是蝴蝶曲线部分
df = sns.load_dataset('iris')
t = np.arange(0.0, 12*np.pi, 0.01)
x = np.sin(t)*(np.e**np.cos(t) - 2*np.cos(4*t)-np.sin(t/12)**5)
y = np.cos(t)*(np.e**np.cos(t) - 2*np.cos(4*t)-np.sin(t/12)**5)
plt.figure(figsize=(8,6))

plt.plot(x,y,color='blue',linewidth = '3')
#######这是分割线部分
plt.axhlines(0, -3, 3,color="red")#横线
plt.axvlines(0, -2, 3,color="red")#竖线

Python

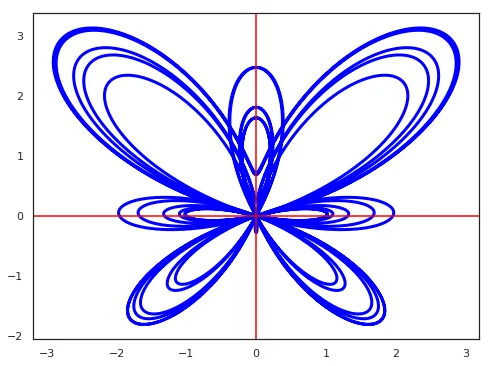
matplotlib.pyplot.axhlines(y, xmin, xmax)表示横线，参数(y的值，横线开始横坐标，横线结束横坐标)

matplotlib.pyplot.axvlines(y, xmin, xmax)表示竖线，参数(x的值，竖线开始纵坐标，竖线结束纵坐标)

总结

matplotlib.pyplot.hlines和matplotlib.pyplot.axhlines都能够画出横线，但是从图中我们可以看到它们是有区别的，hline直线没有接触到坐标轴，axhline接触到了坐标轴。

同理vlines和axvlines同样是垂直线，一个不会接触坐标轴，一个接触坐标轴。

请根据需要选用不同的matplotlib.pyplot函数。

参考来自：https://www.bobobk.com/213.html