对一个点或者向量进行旋转的时候,做法是让这个点(或向量,为了叙述方便,以下只谈论点的情况,向量的情况也是一样的),乘以一个矩阵M,根据之前的知识(参考上一篇blog: https://www.cnblogs.com/heben/p/9182090.html),矩阵M是一个3X3的方阵。
于是点P经过旋转之后,新点P'的坐标计算公式如下:
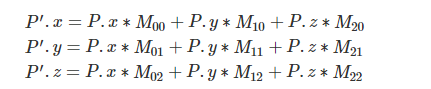
然而这只是旋转。要让P点能够平移,先要思考什么是平移,其实平移就是对P点的每一个坐标加上一个数字,所以带上平移的功能之后,新点P'的坐标应该是下面这样:
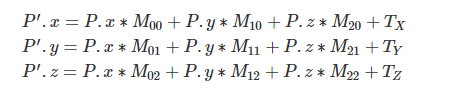
为了将Tx的信息能够存入M矩阵,scratchapixel介绍的方式是,为M矩阵新增一行,将Tx存储为M30,将Ty存储为M31,将Tz存储为M32
于是P'坐标的计算方式就变成:
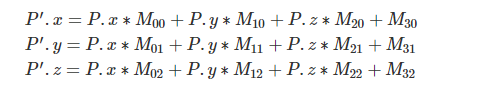
这时M已经成为了一个4X3矩阵,为了满足矩阵的乘法,显然P点也需要改写,写成P(x, y ,z, 1)这样的形式。不过在实际编码中,并不会真的给坐标加上一个第四维度的1,而只是假装那里有个1。点P形式为(x, y, z ,1)的时候,我们称这样的点为同质点(homogeneous point)
最后,CG中常用的M矩阵式4X4的。但这需要了解更多的知识,现在只需要知道,矩阵M由4x3变成4x4,就是新增一列,大部分情况下这一列的数值是(0, 0, 0, 1)