题目大意
一个有向图有起点和终点的有向图,你一次可以走过2^k条边,问从起点到终点所需要走的最小次数。k<=31。
思路
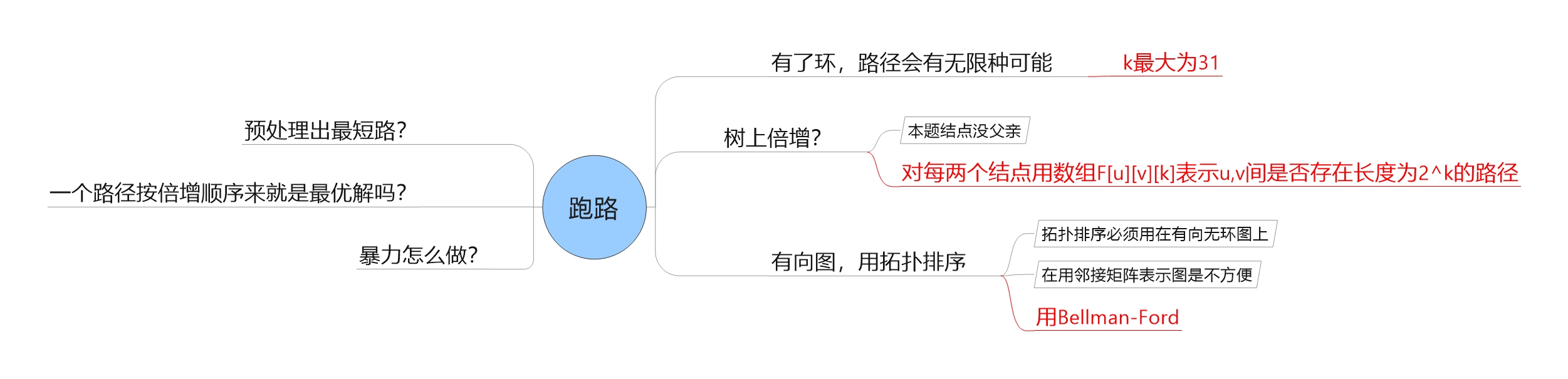
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAX_NODE = 55, MAX_DIGIT = 40, INF = 0x3f3f3f3f;
bool Reachable[MAX_NODE][MAX_NODE][MAX_DIGIT];
int Edges[MAX_NODE][MAX_NODE], Dist[MAX_NODE];
int TotNode, TotEdge;
void B_GetReachable()
{
for (int k = 1; k <= 31; k++)
for (int u = 1; u <= TotNode; u++)
for (int v = 1; v <= TotNode; v++)
for (int mid = 1; mid <= TotNode; mid++)
Reachable[u][v][k] |= (Reachable[u][mid][k - 1] && Reachable[mid][v][k - 1]);
}
void GetEdge()
{
memset(Edges, INF, sizeof(Edges));
for (int k = 0; k <= 31; k++)
for (int u = 1; u <= TotNode; u++)
for (int v = 1; v <= TotNode; v++)
if (Reachable[u][v][k])
Edges[u][v] = 1;
}
void Bellman_Ford()
{
memset(Dist, INF, sizeof(Dist));
Dist[1] = 0;
for (int k = 1; k <= TotNode; k++)
for (int u = 1; u <= TotNode; u++)
for (int v = 1; v <= TotNode; v++)
Dist[v] = min(Dist[v], Dist[u] + Edges[u][v]);
}
int main()
{
scanf("%d%d", &TotNode, &TotEdge);
for (int e = 1; e <= TotEdge; e++)
{
int u, v;
scanf("%d%d", &u, &v);
Reachable[u][v][0] = true;
}
B_GetReachable();
GetEdge();
Bellman_Ford();
printf("%d
", Dist[TotNode]);
return 0;
}