luogu3369 【模板】 普通平衡树 Splay

题目大意

维护一个数据结构，满足以下操作：

1. 插入x数
2. 删除x数(若有多个相同的数，因只删除一个)
3. 查询x数的排名(排名定义为比当前数小的数的个数+1。若有多个相同的数，因输出最小的排名)
4. 查询排名为x的数
5. 求x的前驱(前驱定义为小于x，且最大的数)
6. 求x的后继(后继定义为大于x，且最小的数)

引子

维护一个二叉搜索树，其中每一个节点满足左节点的key小于该节点的key小于等于右节点的key。由于本题要求排名，所以节点中要有值Size表示子树的大小。由于本题要求若有多个相同的数，输出最小的排名，因此每个节点还要维护一个值count表示节点的数值重复了多少次。

但是如果插入的key值是按顺序排列的，整棵树就退化成了一条链，那就没意义了。所以我们用到了Splay。

各个函数解释

Rotate（易错点）

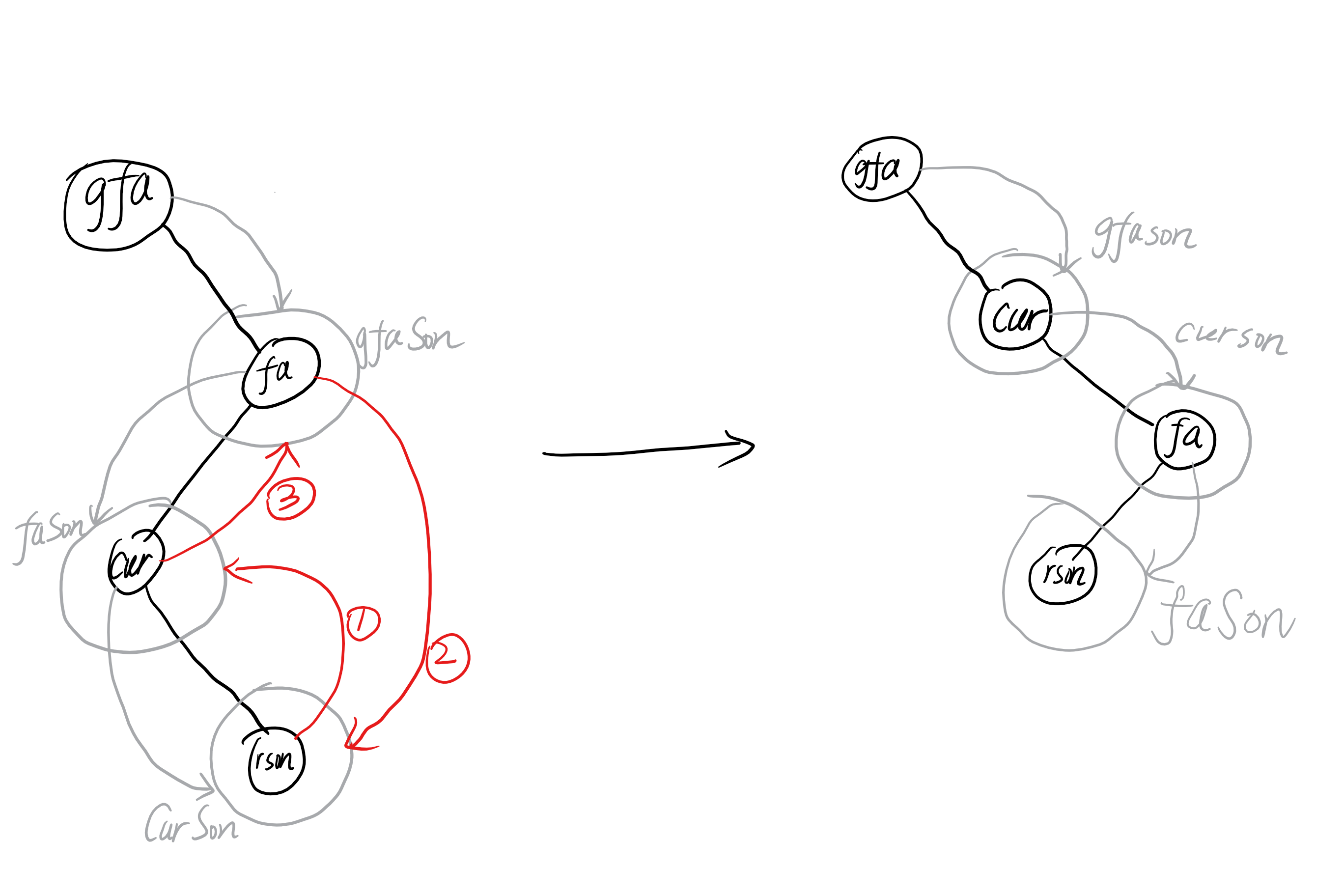
如果我们要Rotate(Node *cur)，就是要达到这样的效果（假设cur为cur->Father->LeftSon）：cur->RightSon到了原先cur->Father->LeftSon的位置（位置faSon），cur->Father到了原先cur->RightSon的位置（位置curSon），cur到了原先cur->Father的位置（位置gfaSon）（这样仍然满足二叉树的数值大小要求）。（如果cur为cur->Father->RightSon则上述内容左右相反。）最后，由于原先cur->Father和cur的子节点变了，所以还要通过一个Refresh函数更新那两个节点的size。

但是由于cur既可能是父亲的左孩子也可能是父亲的右孩子，所以我们根据left和right的不同写两个不同的函数？不用。我们可以用指向节点指针的指针来代表一个节点内存储的不同指针。以后对这个指针的指针操作，就是对原节点内的不同指针的操作。用这种方式表示上文中的三个位置（如果gfa是个空，则gfaSon这个指针的指针就指向Root这个节点的指针，这样就能在Splay中自动对树根进行操作了）。这样可以简化代码。

上图中，黑色部分表示原树，灰色箭头表示指针的指针，灰色圈表示某个情况下指针的指针的值（节点的指针）具体是多少。红色箭头表示操作。

Splay

splay(Node *cur)是要通过旋转操作将节点cur放到顶端。具体操作为：如果节点cur, cur->Father, cur->Father->Father三个节点共线，则先转fa，后转cur，（如果直接只转cur，拿一条链试试，树的最大深度没变）否则只转cur。在插入节点和查找节点时都要进行Splay操作。

Insert

Insert(int key)是要将key插入到树中。首先用二叉树搜索操作查找key值可能存在的节点。如果已经存在key值相等的节点，则将该节点的count值加一即可，否则就要新建一个节点。利用节点指针的指针，我们的节点的指针的指针cur就表示了它到底是父亲的左孩子还是右孩子。

最后要将新结点splay上去。

GetPrevNode

GetPrevNode(Node *cur)是要找到key值比cur小的key值当中最大的key值所对应的结点。找到cur的左孩子，然后不断转移到自己的右孩子去。返回最终的结点。

GetNextNode正好相反。

Find

Find(int key)是要找到key值对应的结点。二叉搜索树的基本操作。

最后要将搜索到的结点Splay上去。

Delete（易错点）

Delete(int key)是要将key值对应结点删除。首先用Find函数找到那个结点。此时，因为Find函数调用了Splay，所以当前结点必然在树顶。此时分情况讨论：

• cur结点count值大于1，则将count值--即可。
• cur只有不多于1个子节点。则将cur存在的那个子节点（如果cur没有子节点，则为NULL）设为树根即可。注意最后要把新树根的Father设为NULL，否则Splay时会判断根节点时会发生错误。
• cur有两个子节点。将GetPrevNode(cur)得到的结点Splay到树根，此时cur必然没有左孩子。这样把新树根与cur的右孩子相连即可。最后要把树的根设为这个新根。

GetRankByKey

得到key的排名。根据每个结点的各个子树大小，进行二叉树搜索即可。

GetKeyByRank

找第rank位的key值。用分治 。左孩子Size大于rank则左找，然后rank<=左孩子Size+点cur的Count刚好，得出结果， 否则向右孩子找，子问题中的rank等于当前的rank -(左孩子size+cur的count)。

GetPrevKey（易忽略点）

GetPrevKey(int key)是要找到严格比key小的Key值。注意题目不保证给出的key值已经加入到树中了。此处注意审题。

具体做法是：向图中加入一个key值结点，然后GetPrevNode那个结点得到结果，最后将新加入的结点删除。

GetNextKey与GetPrevKey相反。

#include <cstdio>
#include <cstring>
#include <cassert>
using namespace std;

const int MAX_NODE = 100010, NoAnswer=0xcfcfcfcf;

struct SplayTree
{
private:
	struct Node
	{
		Node *Father, *LeftSon, *RightSon;
		int Id, Key, Count, Size;

		Node(){}
		Node(int key):Key(key),Count(1),Father(NULL),LeftSon(NULL),RightSon(NULL){}

		bool IsLeftSon()
		{
			assert(Father);
			return Father->LeftSon == this;
		}

		bool IsRoot()
		{
			return Father == NULL || (Father->LeftSon != this &&Father->RightSon != this);
		}

		void Refresh()
		{
			Size = (LeftSon ? LeftSon->Size : 0) + (RightSon ? RightSon->Size : 0) + Count;
		}
	}_nodes[MAX_NODE], *Root;
	int _nodeCnt;

	void SetRoot(Node *cur)
	{
		Root = cur;
		if (Root)
			Root->Father = NULL;
	}

	Node *GetRoot()
	{
		return Root;
	}

	Node *NewNode(int key)
	{
		_nodeCnt++;
		_nodes[_nodeCnt] = Node(key);
		_nodes[_nodeCnt].Id = _nodeCnt;
		return &_nodes[_nodeCnt];
	}

	void Rotate(Node *cur)
	{
		Node *gfa = cur->Father->Father;
		Node **gfaSonP = cur->Father->IsRoot() ? &Root : (cur->Father->IsLeftSon() ? &gfa->LeftSon : &gfa->RightSon);//最好写cur->Father->IsRoot(),而非!Root
		Node **faSonP = cur->IsLeftSon() ? &cur->Father->LeftSon : &cur->Father->RightSon;
		Node **curSonP = cur->IsLeftSon() ? &cur->RightSon : &cur->LeftSon;
		*faSonP = *curSonP;
		if (*faSonP)
			(*faSonP)->Father = cur->Father;
		*curSonP = cur->Father;
		(*curSonP)->Father = cur;
		*gfaSonP = cur;
		(*gfaSonP)->Father = gfa;
		(*curSonP)->Refresh();
		cur->Refresh();
	}

	void PushDown(Node *cur) {}

	void Splay(Node *cur)
	{
		PushDown(cur);//易忘点
		while (!cur->IsRoot())
		{
			if (!cur->Father->IsRoot())
				Rotate(cur->IsLeftSon() == cur->Father->IsLeftSon() ? cur->Father : cur);
			Rotate(cur);
		}
	}

	Node *Find(int key)
	{
		Node *cur = GetRoot();
		if (cur == NULL)
			return NULL;//最好写上
		while (cur)
		{
			if (key == cur->Key)
			{
				Splay(cur);
				return cur;
			}
			cur = key < cur->Key ? cur->LeftSon : cur->RightSon;
		}
		return NULL;
	}

	Node *GetPrevNode(Node *cur)
	{
		if (!(cur = cur->LeftSon))
			return NULL;
		while (cur->RightSon)
			cur = cur->RightSon;
		return cur;
	}

	Node *GetNextNode(Node *cur)
	{
		if (!(cur = cur->RightSon))
			return NULL;
		while (cur->LeftSon)
			cur = cur->LeftSon;
		return cur;
	}

	int GetKeyByRank(Node *cur, int rank)
	{
		if (cur == NULL)
			return NoAnswer;//最好写上
		int leftSize = cur->LeftSon?cur->LeftSon->Size : 0, RootSize;//易忘点：判断
		if (leftSize >= rank)
			return GetKeyByRank(cur->LeftSon, rank);
		else if ((RootSize = leftSize + cur->Count) >= rank)
			return cur->Key;
		else
			return GetKeyByRank(cur->RightSon, rank - RootSize);
	}

public:
	SplayTree()
	{
		memset(_nodes, 0, sizeof(_nodes));
		_nodeCnt = 0;
	}

	void Insert(int key)
	{
		Node **curP = &Root;
		Node *fa = NULL;
		while (*curP && (*curP)->Key != key)
		{
			fa = *curP;
			curP = key < (*curP)->Key ? &(*curP)->LeftSon : &(*curP)->RightSon;
		}
		if (*curP)
			(*curP)->Count++;
		else
		{
			*curP = NewNode(key);
			(*curP)->Father = fa;//此处不必cur->Father->Refresh()是因为下面Splay设置好了。
		}
		Splay(*curP);//易忘点
	}

	void Delete(int key)
	{
		Node *cur = Find(key);
		if (cur->Count > 1)
			cur->Count--;
		else if (!cur->LeftSon || !cur->RightSon)
			SetRoot(cur->LeftSon ? cur->LeftSon : cur->RightSon);
		else if (cur->LeftSon&&cur->RightSon)
		{
			Node *root = GetPrevNode(cur);
			Splay(root);
			root->RightSon = cur->RightSon;
			if (cur->RightSon)//易忘点
				cur->RightSon->Father = root;
		}
	}

	int GetRankByKey(int key)
	{
		Node *cur = Find(key);
		if (cur == NULL)
			return NoAnswer;
		return (cur->LeftSon ? cur->LeftSon->Size : 0) + 1;
	}

	int GetKeyByRank(int rank)
	{
		return GetKeyByRank(Root, rank);
	}

	int GetPrevKey(int key)
	{
		Insert(key);
		int ans = GetPrevNode(Find(key))->Key;
		Delete(key);
		return ans;
	}

	int GetNextKey(int key)
	{
		Insert(key);
		int ans = GetNextNode(Find(key))->Key;
		Delete(key);
		return ans;
	}
}g;

int main()
{
	int opCnt, op, key, rank;
	scanf("%d", &opCnt);
	while (opCnt--)
	{
		scanf("%d", &op);
		switch (op)
		{
		case 1://Insert
			scanf("%d", &key);
			g.Insert(key);
			break;
		case 2://Delete
			scanf("%d", &key);
			g.Delete(key);
			break;
		case 3://GetRankByKey
			scanf("%d", &key);
			printf("%d
", g.GetRankByKey(key));
			break;
		case 4://GetKeyByRank
			scanf("%d", &rank);
			printf("%d
", g.GetKeyByRank(rank));
			break;
		case 5://GetPrevKey
			scanf("%d", &key);
			printf("%d
", g.GetPrevKey(key));
			break;
		case 6://GetNextKey
			scanf("%d", &key);
			printf("%d
", g.GetNextKey(key));
			break;
		}
	}
	return 0;
}