集合的子集输出（位运算方式）

问题：怎样找出某个集合的所有子集，怎样找出某个集合指定元素个数的所有子集？

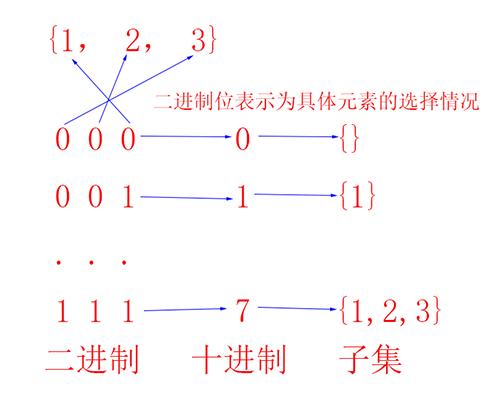
思路：对集合中所有元素进行标记，0表示未选中，1表示选中。假如有一个集合有3个元素为 {1,2,3}, 则 000 表示一个都不选， 001表示选中数组中第一个元素1，010表示选中数组中第2个元素2，011表示选中数组中第1,2个元素即是1,2...。 这样一来，集合{1,2,3}的所有子集（忽略空集）可以表示为 001 -> 111 这样的编码。这样，我们就知道集合的所有子集的个数，即是 2^3=8个。所以，如果我们需要输出所有的子集，只需要将每个子集用 001这样的二进制编码表示，然后按照此编码输出选中的元素即可。十进制1->7恰可表示为二进制001->111这样的编码，这样求集合的所有子集就很简单了，所有的子集就是： 0->(2^元素数-1) 表示为二进制编码 所对应的集合元素的选择! 

实现：

package com.hdwang;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * Created by hdwang on 2016-12-29.
 * 集合中输出所有子集（空集除外），或者输出指定元素个数的子集
 * 思路：对每个元素进行标记（选择1 不选0），穷举子集，穷举中可进行筛选
 */
public class Combine2 {

    /**
     * 集合
     */
    private int data[] = {1, 2, 3, 4, 5, 6, 7, 8};

    Combine2(int size){
        //初始化集合
        this.data = new int[size];
        for(int i=0;i<size;i++){
            this.data[i] = i+1;
        }
        System.out.println("集合是:"+ Arrays.toString(this.data));
    }

    /**
     * 组合子集
     */
    List<String> subColListCH = new ArrayList<String>();

    /**
     * 输出集合的所有子集（空集忽略）
     */
    public void generateAllSubCol(){
        //256表示8个元素的输出情况
        for(int i = 1; i < 256; i++)   // 2^8 = 256
        {
            System.out.print(i+ " : ");
            int mark = 1;
            for(int j = 0; j < 8; j++)
            {
                int index = mark & i;  //mark与i后 得到i的每一位
                if(0 != index)         // 该位置是1，状态是选中，则输出对应元素
                {
                    System.out.print(data[j]+ " ");
                }
                mark <<= 1;  //mark在内层循环中，每次的值为1,2,4,8,16,32,64,128
            }
            System.out.println();
        }
    }

    /**
     * 输出指定元素个数的子集
     * @param subSize 子集大小
     */
    public void generateSubCol(int subSize){
        System.out.println("子集大小是："+subSize);

        int elCount = data.length; //元素个数
        int allSubColCount = (int)Math.pow(2,elCount); //子集个数（空集不算）

        for(int i=1;i<allSubColCount;i++){ //i表示了一个子集的输出规则
            int mark = 1; //用于取出i的每一位
            List<Integer> subCol = new ArrayList(); //存储子集元素

            for(int j=0; j<elCount; j++){
                int index = mark & i; //取出i的第1位，第2位。。。
                if(0 != index){
                    subCol.add(data[j]);
                }
                mark <<= 1; //mark左移1位，用于获取i高一位的数字
            }

            if(subCol.size() == subSize){ //子集元素个数符合要求
                subColListCH.add(listToString(subCol, ','));
            }
        }

        System.out.println("
打印组合集合:size is "+this.subColListCH.size());
        for(int i=0;i< this.subColListCH.size();i++) {
            String line = subColListCH.get(i);
            System.out.println(line);
        }
    }

    /**
     * list转换字符串
     * @param list list
     * @param separator 分隔符
     * @return 字符串
     */
    public String listToString(List list, char separator) {
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < list.size(); i++) {
            sb.append(list.get(i)).append(separator);
        }
        return sb.toString().substring(0,sb.toString().length()-1);
    }
}

函数调用

Combine2 combine2 = new Combine2(3);
combine2.generateSubCol(2);

输出结果

集合是:[1, 2, 3]
子集大小是：2

打印组合集合:size is 3
1,2
1,3
2,3