作者:Vamei 出处:http://www.cnblogs.com/vamei 欢迎转载,也请保留这段声明。谢谢!
堆(heap)又被为优先队列(priority queue)。尽管名为优先队列,但堆并不是队列。回忆一下,在队列中,我们可以进行的限定操作是dequeue和enqueue。dequeue是按照进入队列的先后顺序来取出元素。而在堆中,我们不是按照元素进入队列的先后顺序取出元素的,而是按照元素的优先级取出元素。
这就好像候机的时候,无论谁先到达候机厅,总是头等舱的乘客先登机,然后是商务舱的乘客,最后是经济舱的乘客。每个乘客都有头等舱、商务舱、经济舱三种个键值(key)中的一个。头等舱->商务舱->经济舱依次享有从高到低的优先级。
再比如,封建社会的等级制度,也是一个堆。在这个堆中,国王、贵族、骑士和农民是从高到低的优先级。
封建等级
Linux内核中的调度器(scheduler)会按照各个进程的优先级来安排CPU执行哪一个进程。计算机中通常有多个进程,每个进程有不同的优先级(该优先级的计算会综合多个因素,比如进程所需要耗费的时间,进程已经等待的时间,用户的优先级,用户设定的进程优先程度等等)。内核会找到优先级最高的进程,并执行。如果有优先级更高的进程被提交,那么调度器会转而安排该进程运行。优先级比较低的进程则会等待。“堆”是实现调度器的理想数据结构。
(Linux中可以使用nice命令来影响进程的优先级)
堆的实现
堆的一个经典的实现是完全二叉树(complete binary tree)。这样实现的堆成为二叉堆(binary heap)。
完全二叉树是增加了限定条件的二叉树。假设一个二叉树的深度为n。为了满足完全二叉树的要求,该二叉树的前n-1层必须填满,第n层也必须按照从左到右的顺序被填满,比如下图:
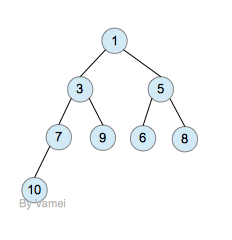
为了实现堆的操作,我们额外增加一个要求: 任意节点的优先级不小于它的子节点。如果在上图中,设定小的元素值享有高的优先级,那么上图就符合该要求。
这类似于“叠罗汉”。叠罗汉最重要的一点,就是让体重大的参与者站在最下面,让体重小的参与者站在上面 (体重小,优先级高)。为了让“堆”稳固,我们每次只允许最上面的参与者退出堆。也就是,每次取出的优先级最高的元素。

三个“叠罗汉”堆
我已经在排序算法简介及其C实现中实际使用了堆。堆的主要操作是插入和删除最小元素(元素值本身为优先级键值,小元素享有高优先级)。在插入或者删除操作之后,我们必须保持该实现应有的性质: 1. 完全二叉树 2. 每个节点值都小于或等于它的子节点。
在插入操作的时候,会破坏上述堆的性质,所以需要进行名为percolate_up的操作,以进行恢复。新插入的节点new放在完全二叉树最后的位置,再和父节点比较。如果new节点比父节点小,那么交换两者。交换之后,继续和新的父节点比较…… 直到new节点不比父节点小,或者new节点成为根节点。这样得到的树,就恢复了堆的性质。
我们插入节点2:
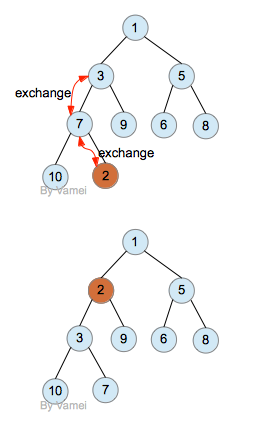
插入
删除操作只能删除根节点。根节点删除后,我们会有两个子树,我们需要基于它们重构堆。进行percolate_down的操作: 让最后一个节点last成为新的节点,从而构成一个新的二叉树。再将last节点不断的和子节点比较。如果last节点比两个子节点中小的那一个大,则和该子节点交换。直到last节点不大于任一子节点都小,或者last节点成为叶节点。
删除根节点1。如图:

删除根节点
下面是代码。与我们在二叉搜索树中使用表不同,我们这里使用数组来表示完全二叉树。数组下标为0的元素不用于储存节点,而用于记录完全二叉树中元素的总数。
/* By Vamei
Use an big array to implement heap
DECLARE: int heap[MAXSIZE] in calling function
heap[0] : total nodes in the heap
for a node i, its children are i*2 and i*2+1 (if exists)
its parent is i/2 */
void insert(int new, int heap[])
{
int childIdx, parentIdx;
heap[0] = heap[0] + 1;
heap[heap[0]] = new;
/* recover heap property */
percolate_up(heap);
}
static void percolate_up(int heap[]) {
int lightIdx, parentIdx;
lightIdx = heap[0];
parentIdx = lightIdx/2;
/* lightIdx is root? && swap? */
while((parentIdx > 0) && (heap[lightIdx] < heap[parentIdx])) {
/* swap */
swap(heap + lightIdx, heap + parentIdx);
lightIdx = parentIdx;
parentIdx = lightIdx/2;
}
}
int delete_min(int heap[])
{
int min;
if (heap[0] < 1) {
/* delete element from an empty heap */
printf("Error: delete_min from an empty heap.");
exit(1);
}
/* delete root
move the last leaf to the root */
min = heap[1];
swap(heap + 1, heap + heap[0]);
heap[0] -= 1;
/* recover heap property */
percolate_down(heap);
return min;
}
static void percolate_down(int heap[]) {
int heavyIdx;
int childIdx1, childIdx2, minIdx;
int sign; /* state variable, 1: swap; 0: no swap */
heavyIdx = 1;
do {
sign = 0;
childIdx1 = heavyIdx*2;
childIdx2 = childIdx1 + 1;
if (childIdx1 > heap[0]) {
/* both children are null */
break;
}
else if (childIdx2 > heap[0]) {
/* right children is null */
minIdx = childIdx1;
}
else {
minIdx = (heap[childIdx1] < heap[childIdx2]) ?
childIdx1 : childIdx2;
}
if (heap[heavyIdx] > heap[minIdx]) {
/* swap with child */
swap(heap + heavyIdx, heap + minIdx);
heavyIdx = minIdx;
sign = 1;
}
} while(sign == 1);
}
你可以尝试一下构建自己的main函数,测试相关的操作。
总结
堆,优先级
插入元素,删除最大优先级元素
