题目:To My Girlfriend
链接:http://acm.hdu.edu.cn/showproblem.php?pid=5800
题意:
给你n、s,接下来n个数,定义 f ( i , j , k , l , m )表示下标为i、j的必选,k、l的必不选,且和为m的 子集 数量。
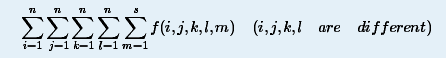
然后求上图式子的值。
思路:
刚开始想着i 个数的和小于等于s 的子集数量,定义了dp[i][j]表示i 个数,和为j 的情况数量,不管怎么优化死活要n^3级别。看了题解,才觉醒。。。
定义dp[i][j][ii][jj]表示:前i个数中,和达到j,ii个必选,jj个必不选的情况数量。ii、jj范围为0-2,四重循环就可以了。
分两种:
1. 第i 个数可选可不选,那么dp[i][j][ii][jj] += dp[i-1][j][ii][jj] + dp[i-1][j-a[i]][ii][jj]。
2. 又分两种:
1. 第i个数必选,dp[i][j][ii][jj] += dp[i-1][j-a[i]][ii-1][jj]。
2. 第i个数必不选,dp[i][j][ii][jj] += dp[i-1][j][ii][jj-1]。
AC代码:
1 #include<stdio.h>
2 #include<string.h>
3 #define Mod 1000000007
4 typedef long long LL;
5 int a[1010];
6 int dp[1010][1010][3][3];
7 void add(int &x,int y)
8 {
9 x=x+y;
10 if(x>=Mod) x-=Mod;
11 }
12 int main()
13 {
14 int t,n,m;
15 scanf("%d",&t);
16 while(t--)
17 {
18 scanf("%d%d",&n,&m);
19 for(int i=1;i<=n;i++) scanf("%d",&a[i]);
20 memset(dp,0,sizeof(dp));
21 dp[0][0][0][0]=1;
22 for(int i=1;i<=n;i++)
23 {
24 for(int j=m;j>=0;j--)
25 {
26 for(int ii=2;ii>=0;ii--)
27 {
28 for(int jj=2;jj>=0;jj--)
29 {
30 add( dp[i][j][ii][jj] , dp[i-1][j][ii][jj] );
31 if(j+a[i]<=m) add( dp[i][j+a[i]][ii][jj] , dp[i-1][j][ii][jj] );
32 if(ii > 0 && j+a[i]<=m) add( dp[i][j+a[i]][ii][jj] , dp[i-1][j][ii-1][jj] );
33 if(jj > 0) add( dp[i][j][ii][jj] , dp[i-1][j][ii][jj-1] );
34 }
35 }
36 }
37 }
38 LL ret=0;
39 for(int i=2;i<=m;i++)
40 {
41 ret=ret+dp[n][i][2][2];
42 }
43 printf("%I64d
",ret*2*2%Mod);
44 }
45 return 0;
46 }