Loj #2568. 「APIO2016」烟花表演
题目描述
烟花表演是最引人注目的节日活动之一。在表演中,所有的烟花必须同时爆炸。为了确保安全,烟花被安置在远离开关的位置上,通过一些导火索与开关相连。导火索的连接方式形成一棵树,烟花是树叶,如图 1所示。火花从开关出发,沿导火索移动。每当火花抵达一个分叉点时,它会扩散到与之相连的所有导火索,继续燃烧。导火索燃烧的速度是一个固定常数。图 1展示了六枚烟花 ({E_1, E_2, ldots, E_6 }) 的连线布局,以及每根导火索的长度。图中还标注了当在时刻 (0) 从开关点燃火花时,每一发烟花的爆炸时间。
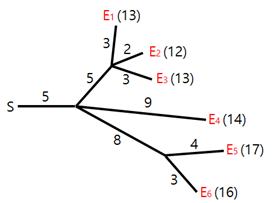
Hyunmin 为烟花表演设计了导火索的连线布局。不幸的是,在他设计的布局中,烟花不一定同时爆炸。我们希望修改一些导火索的长度,让所有烟花在同一时刻爆炸。例如,为了让图 1中的所有烟花在时刻 (13) 爆炸,我们可以像图 2中左边那样调整导火索长度。类似地,为了让图 1中的所有烟花在时刻 (14) 爆炸,我们可以像图 2中右边那样调整长度。
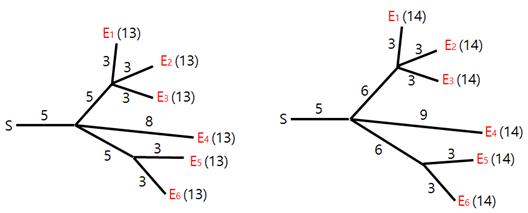
修改导火索长度的代价等于修改前后长度之差的绝对值。例如,将图 1中布局修改为图 2,左边布局的总代价为 (6),而将图 1中布局修改为图 2右边布局的总代价为 (5)。
导火索的长度可以被减为 (0),同时保持连通性不变。
给定一个导火索的连线布局,你需要编写一个程序,去调整导火索长度,让所有的烟花在同一时刻爆炸,并使得代价最小。
输入格式
所有的输入均为正整数。令 (N) 代表分叉点的数量,(M) 代表烟花的数量。分叉点从 (1) 到 (N) 编号,编号为 (1) 的分叉点是开关。烟花从 (N+1) 到 (N+M) 编号。
输入格式如下:
(N::M)
(P_2::C_2)
(P_3::C_3)
(ldots)
(P_N::C_N)
(P_{N+1}::C_{N+1})
(ldots)
(P_{N+M}::C_{N+M})
其中 (P_i) 满足 (1le P_i<i),代表和分叉点或烟花 (i) 相连的分叉点。(C_i) 代表连接它们的导火索长度 ((1le C_ile 10^9))。除开关外,每个分叉点和多于 (1) 条导火索相连,而每发烟花恰好与 (1) 条导火索相连。
数据范围与提示
子任务 1(7 分):(N=1,1 le M le 100)。
子任务 2(19 分):(1 le N+M le 300),且开关到任一烟花的距离不超过 (300)。
子任务 3(29 分):(1 le N+M le 5000)。
子任务 4(45 分):(1 le N+M le 3 imes 10^5)。
(\)
设(f_i(x))为使得(i)的子树中所有叶子到(i)距离为(x)所付出的代价。很明显(f_i(x))是个下凸的函数,而且中间有一整段斜率为(0)的区间,假设为([L,R])。我们先考虑已经得到了(f_u(x)),要加上(u)的父亲到(u)的那条边(长度为(w))后函数怎么变化。
假设最终这条边的边权为(w'),最优策略就是尽量使得(x-w'),也就是所有叶子到(u)的距离尽量往([L,R])靠。
我们观察这个转移,相当于将(L)以左的部分抬高(w),然后接一条斜率为(-1)的直线,然后接一条斜率为(0)的直线,最后接斜率为(1)的直线。也就是说先将右端的斜率大于(0)的直线全部删除,再加入上述三条直线。
假设我们已经完成了这个操作,于是就把这个函数加到(fa_u)的函数中。我们发现累加函数会使斜率逐渐增大。比如函数(1)在(xgeq x_1)的部分斜率为(1),函数(2)在(xgeq x_2)的部分斜率为(1)((x_1<x_2)),那么新函数在(x_1leq xleq x_2)的部分斜率为(1),在(x>x_2)的部分斜率为(2)。
所以我们只需要维护函数的拐点的横坐标就行了。考虑每合并一个儿子,函数的最大斜率都会(+1),所以函数最右端斜率(>0)的端点个数就是儿子的数量。具体实现可以用可并堆。
最后考虑得到最终的函数后怎么算答案。明显答案就在那一段斜率为(0)的区间,但是我们只维护了横坐标。我们知道(f_1(0)=sum),其中(sum)表示所有的边长度之和。每次合并函数,最大斜率(+1),同理最小斜率也会(-1),所有函数左侧的斜率也是递减的。假设最左侧斜率(<0)的一堆端点有(k)个,分别为(x_1,x_2,ldots,x_k),那么答案就
代码:
#include<bits/stdc++.h>
#define ll long long
#define N 600005
using namespace std;
inline int Get() {int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}while('0'<=ch&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}return x*f;}
int n,m;
struct tree {
int ls,rs,key;
ll val;
}tr[N<<1];
int Merge(int a,int b) {
if(!a||!b) return a+b;
if(tr[a].val<tr[b].val) swap(a,b);
tr[a].rs=Merge(tr[a].rs,b);
if(tr[tr[a].ls].key<tr[tr[a].rs].key) swap(tr[a].ls,tr[a].rs);
tr[a].key=tr[a].rs?tr[tr[a].rs].key+1:0;
return a;
}
int Pop(int a) {return Merge(tr[a].ls,tr[a].rs);}
int fa[N];
int len[N];
ll sum;
int sn[N];
int rt[N];
int tot;
int main() {
n=Get(),m=Get();
for(int i=2;i<=n+m;i++) {
fa[i]=Get(),len[i]=Get();
sum+=len[i];
sn[fa[i]]++;
}
for(int i=n+m;i>=2;i--) {
ll l=0,r=0;
if(i<=n) {
while(--sn[i]) rt[i]=Pop(rt[i]);
r=tr[rt[i]].val;rt[i]=Pop(rt[i]);
l=tr[rt[i]].val;rt[i]=Pop(rt[i]);
}
tr[++tot].val=l+len[i];
tr[++tot].val=r+len[i];
rt[i]=Merge(rt[i],Merge(tot-1,tot));
rt[fa[i]]=Merge(rt[fa[i]],rt[i]);
}
while(sn[1]--) rt[1]=Pop(rt[1]);
while(rt[1]) {
sum-=tr[rt[1]].val;
rt[1]=Pop(rt[1]);
}
cout<<sum;
return 0;
}