问题描述
Fibonacci数列的递推公式为:Fn=Fn-1+Fn-2,其中F1=F2=1。
当n比较大时,Fn也非常大,现在我们想知道,Fn除以10007的余数是多少。
输入格式
输入包含一个整数n。
输出格式
输出一行,包含一个整数,表示Fn除以10007的余数。
说明:在本题中,答案是要求Fn除以10007的余数,因此我们只要能算出这个余数即可,而不需要先计算出Fn的准确值,再将计算的结果除以10007取余数,直接计算余数往往比先算出原数再取余简单。
样例输入
10
样例输出
55
样例输入
22
样例输出
7704
数据规模与约定
1 <= n <= 1,000,000。
1 #include<iostream> 2 using namespace std; 3 4 long long a[1000005]; 5 int main(){ 6 int n; 7 cin>>n; 8 a[1] = 1; 9 a[2] = 1; 10 for(int i=3;i<=n;i++){ 11 a[i] = (a[i-1]+a[i-2])%10007; 12 } 13 cout<<a[n]; 14 return 0; 15 } 16
推广:
问题描述
斐波那契数列大家都非常熟悉。它的定义是:
f(x) = 1 .... (x=1,2)
f(x) = f(x-1) + f(x-2) .... (x>2)
对于给定的整数 n 和 m,我们希望求出:
f(1) + f(2) + ... + f(n) 的值。但这个值可能非常大,所以我们把它对 f(m) 取模。
公式如下
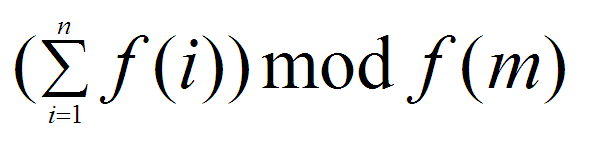
但这个数字依然很大,所以需要再对 p 求模。
f(x) = 1 .... (x=1,2)
f(x) = f(x-1) + f(x-2) .... (x>2)
对于给定的整数 n 和 m,我们希望求出:
f(1) + f(2) + ... + f(n) 的值。但这个值可能非常大,所以我们把它对 f(m) 取模。
公式如下
但这个数字依然很大,所以需要再对 p 求模。
输入格式
输入为一行用空格分开的整数 n m p (0 < n, m, p < 10^18)
输出格式
输出为1个整数,表示答案
样例输入
2 3 5
样例输出
0
样例输入
15 11 29
样例输出
25
1 #include<iostream> 2 using namespace std; 3 int main() 4 { 5 long long i,j,n,m,p,a,b,c,fm,sn,result; 6 cin>>n>>m>>p; 7 a=b=1; 8 for(i=3;i<=m;i++)//求fm 9 { 10 c=a+b; 11 a=b; 12 b=c; 13 } 14 fm=b; 15 a=b=1; 16 for(i=3;i<=n+2;i++)//求sn 17 { 18 if(a+b>=fm) 19 c=(a+b)%fm; 20 else 21 c=a+b; 22 a=b; 23 b=c; 24 } 25 sn=(b+fm-1)%fm; 26 result=sn%p; 27 cout<<result<<endl; 28 return 0; 29 }
自己写的代码只能过20%的数据,上面是别人写的,能过40%的数,找了半天也没找到满分的。。。。