【人工智能导论：模型与算法】MOOC 8.3 误差后向传播(BP) 例题 【第三版】

第一版：完全按照MOOC课件编程实现

【人工智能导论：模型与算法】MOOC 8.3 误差后向传播(BP) 例题 编程验证 - HBU_DAVID - 博客园 (cnblogs.com)

第二版：用PyTorch实现，发现求得梯度与MOOC课件不一致

怀疑程序有Bug，感觉肯是对 l.backward（）有理解不到位的地方：

【人工智能导论：模型与算法】MOOC 8.3 误差后向传播(BP) 例题 编程验证 Pytorch版本 - HBU_DAVID - 博客园 (cnblogs.com)

研究代码很久，找不到问题所在。求助 Ma xiaotian & Jiang ruohui 。

 Ma xiaotian ：经过推导发现MOOC教材推导有错误。w1 - w4 公式第三步有错。所以计算结果也是错的。Pytorch计算的是对的。 

 

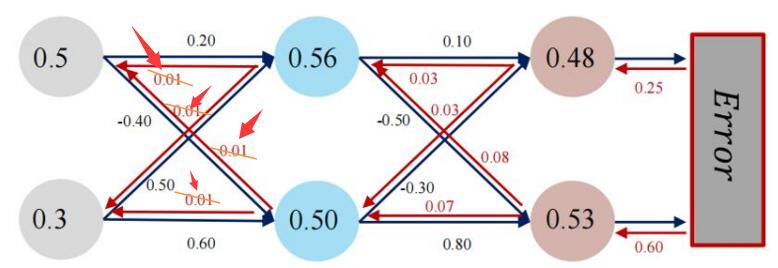
 终于破案了！

---

 

第一版本（MOOC手推反向传播）更正后的程序：

查看代码

import numpy as np

w1, w2, w3, w4, w5, w6, w7, w8 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8
x1, x2 = 0.5, 0.3
y1, y2 = 0.23, -0.07
print("输入值 x0, x1:", x1, x2)
print("输出值 y0, y1:", y1, y2)


def sigmoid(z):
    a = 1 / (1 + np.exp(-z))
    return a


def forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8):
    in_h1 = w1 * x1 + w3 * x2
    out_h1 = sigmoid(in_h1)
    in_h2 = w2 * x1 + w4 * x2
    out_h2 = sigmoid(in_h2)

    in_o1 = w5 * out_h1 + w7 * out_h2
    out_o1 = sigmoid(in_o1)
    in_o2 = w6 * out_h1 + w8 * out_h2
    out_o2 = sigmoid(in_o2)

    print("正向计算，隐藏层h1 ,h2：", end="")
    print(round(out_h1, 5), round(out_h2, 5))
    print("正向计算，预测值o1 ,o2：", end="")
    print(round(out_o1, 5), round(out_o2, 5))

    error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2

    print("损失函数(均方误差)：",round(error, 5))

    return out_o1, out_o2, out_h1, out_h2


def back_propagate(out_o1, out_o2, out_h1, out_h2):
    # 反向传播
    d_o1 = out_o1 - y1
    d_o2 = out_o2 - y2

    d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
    d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
    d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
    d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2

    d_w1 = (d_o1 * out_h1 * (1 - out_h1) * w5 + d_o2 * out_o2 * (1 - out_o2) * w6) * out_h1 * (1 - out_h1) * x1
    d_w3 = (d_o1 * out_h1 * (1 - out_h1) * w5 + d_o2 * out_o2 * (1 - out_o2) * w6) * out_h1 * (1 - out_h1) * x2
    d_w2 = (d_o1 * out_h1 * (1 - out_h1) * w7 + d_o2 * out_o2 * (1 - out_o2) * w8) * out_h2 * (1 - out_h2) * x1
    d_w4 = (d_o1 * out_h1 * (1 - out_h1) * w7 + d_o2 * out_o2 * (1 - out_o2) * w8) * out_h2 * (1 - out_h2) * x2

    print("w的梯度:",round(d_w1, 2), round(d_w2, 2), round(d_w3, 2), round(d_w4, 2), round(d_w5, 2), round(d_w6, 2),
          round(d_w7, 2), round(d_w8, 2))

    return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8


def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
    # 步长
    step = 1
    w1 = w1 - step * d_w1
    w2 = w2 - step * d_w2
    w3 = w3 - step * d_w3
    w4 = w4 - step * d_w4
    w5 = w5 - step * d_w5
    w6 = w6 - step * d_w6
    w7 = w7 - step * d_w7
    w8 = w8 - step * d_w8
    return w1, w2, w3, w4, w5, w6, w7, w8


if __name__ == "__main__":

    print("权值w0-w7:",round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
          round(w8, 2))


    for i in range(1):
        print("=====第" + str(i+1) + "轮=====")
        out_o1, out_o2, out_h1, out_h2 = forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8)
        d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8 = back_propagate(out_o1, out_o2, out_h1, out_h2)
        w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)

    print("更新后的权值w:",round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
          round(w8, 2))

运行结果：

第二版本（pytorch版本）：

查看代码

import torch

x = [0.5, 0.3]  # x0, x1 = 0.5, 0.3
y = [0.23, -0.07]  # y0, y1 = 0.23, -0.07
print("输入值 x0, x1:", x[0], x[1])
print("输出值 y0, y1:", y[0], y[1])
w = [torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
    [0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8])]  # 权重初始值
for i in range(0, 8):
    w[i].requires_grad = True
print("权值w0-w7:")
for i in range(0, 8):
    print(w[i].data, end="  ")


def forward_propagate(x):  # 计算图
    in_h1 = w[0] * x[0] + w[2] * x[1]
    out_h1 = torch.sigmoid(in_h1)
    in_h2 = w[1] * x[0] + w[3] * x[1]
    out_h2 = torch.sigmoid(in_h2)

    in_o1 = w[4] * out_h1 + w[6] * out_h2
    out_o1 = torch.sigmoid(in_o1)
    in_o2 = w[5] * out_h1 + w[7] * out_h2
    out_o2 = torch.sigmoid(in_o2)

    print("正向计算，隐藏层h1 ,h2：", end="")
    print(out_h1.data, out_h2.data)
    print("正向计算，预测值o1 ,o2：", end="")
    print(out_o1.data, out_o2.data)

    return out_o1, out_o2


def loss(x, y):  # 损失函数
    y_pre = forward_propagate(x)  # 前向传播
    loss_mse = (1 / 2) * (y_pre[0] - y[0]) ** 2 + (1 / 2) * (y_pre[1] - y[1]) ** 2  # 考虑 ： t.nn.MSELoss()
    print("损失函数(均方误差)：", loss_mse.item())
    return loss_mse


if __name__ == "__main__":
    for k in range(1):
        print("\n=====第" + str(k+1) + "轮=====")
        l = loss(x, y)  # 前向传播，求 Loss，构建计算图
        l.backward()  # 反向传播，求出计算图中所有梯度存入w中. 自动求梯度，不需要人工编程实现。
        print("w的梯度: ", end="  ")
        for i in range(0, 8):
            print(round(w[i].grad.item(), 2), end="  ")  # 查看梯度
        step = 1  # 步长
        for i in range(0, 8):
            w[i].data = w[i].data - step * w[i].grad.data  # 更新权值
            w[i].grad.data.zero_()  # 注意：将w中所有梯度清零
        print("\n更新后的权值w:")
        for i in range(0, 8):
            print(w[i].data, end="  ")

运行结果：

 

---

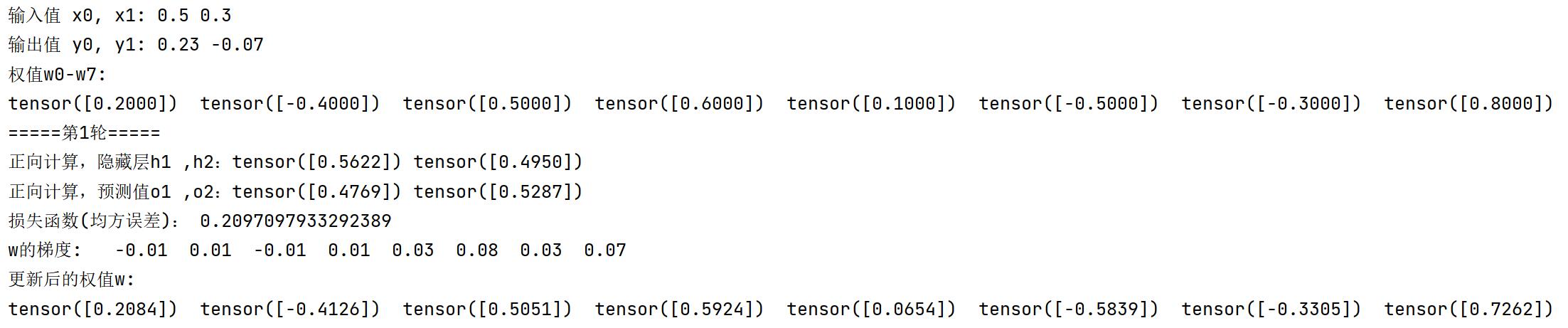
训练10轮后，手推版VS.Pytorch版：损失函数，梯度均相等

---

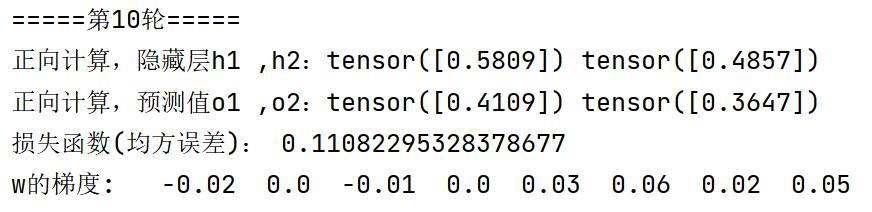
训练100轮后，手推版VS.Pytorch版：损失函数，梯度均相等

---

【总结】

1. 使用Pytorch得到了与手推相等结果，验证了pytorch中backward（）的正确性。
2. Pytorch不用编程实现bp，直接调用backward（）完成，提高了效率。深层网络，人工计算既麻烦又容易出错，框架帮助人们解决了问题。
3. 通过手推版程序，了解反向传播过程，有助于理解backward（）的实现。
4. 学习了计算图、自动微分在pytorch中的实现过程。
5. 对MOOC的内容不能掉以轻心。同时证明了2中所述：人工计算既麻烦又容易出错。这么简单的网络，人工计算都有失误，何况更深的网络。
6. 感谢Ma xiaotian、Jiang ruohui 同学的帮助。不然会一直在研究程序，而不考虑MOOC内容有错。这样显然是行不通的，方向错了，再努力也没有用~