这一部分吴飞老师讲解了贝叶斯公式的使用,顺道复习一下概率知识
A 为 条件 | 特征;B 为 标签 | 分类
先验概率:是指根据以往经验和分析得到的概率,它往往作为"由因求果"问题中的"因"出现的概率。P(A)
后验概率:在得到“结果”的信息后重新修正的概率,是“执果寻因”问题中的"果"。后验概率可以根据通过贝叶斯公式,用先验概率和似然函数计算出来。P(B|A)
后验概率是一种条件概率,但是与其它条件概率的不同之处在于,它限定了目标事件为隐变量取值,而其中的条件为观测结果。
条件概率:一个事件发生后另一个事件发生的概率。P(B|A)
似然概率:似然函数可以理解为条件概率的逆反。P(A|B)

联合概率:包含多个条件且所有条件同时成立的概率。既满足 X 条件,又满足 Y 条件的概率 。P(A,B)
边缘概率:边缘概率是与联合概率对应的。P(X=a)或P(Y=b),这类仅与单个随机变量有关的概率称为边缘概率。
是某个事件发生的概率,而与其它事件无关。
边缘概率是这样得到的:在联合概率中,把最终结果中不需要的那些事件合并成其事件的全概率而消失(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率)。



全概率
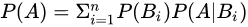
贝叶斯公式

贝叶斯分类 忽略分母:
对于所有分类,分母的取值始终是相等的。
分类的时候比较大小,省略掉“分母”,对结果没有影响,可以忽略。
这样可以省去计算全概率的步骤。
ref:
https://blog.csdn.net/liuweiyuxiang/article/details/89741195
https://blog.csdn.net/tick_tock97/article/details/79885868
https://blog.csdn.net/tick_tock97/article/details/79885868#commentBox
https://zhuanlan.zhihu.com/p/53005534
https://blog.csdn.net/songyu0120/article/details/85059149
https://www.zhihu.com/question/22905989
https://blog.csdn.net/qq_29407397/article/details/88690240
https://zhuanlan.zhihu.com/p/110402052
https://zhuanlan.zhihu.com/p/57446474