• 最近公共祖先

    最近公共祖先(LCA)

    1. 概念

    • 对于有根树T的两个结点u,v，最近公共祖先LCA(T,u,v)表示一个结点x，满足x是u,v的深度最大的祖先节点。
    • LCA算法分为离线算法和在线算法
      • 离线算法( off line algorithms)，是指基于在执行算法前输入数据已知的基本假设，也就是说，对于一个离线算法，在开始时就需要知道问题的所有输入数据，而且在解决一个问题后就要立即输出结果。
      • 在线算法是指它可以以序列化的方式一个个的处理输入，也就是说在开始时并不需要已经知道所有的输入。
    • LCA的离线算法主要指的是基于深度优先搜索的tarjan算法

    2. tarjan求LCA

    • 实现步骤：

      1. 任选一个点u为根节点，从根节点开始DFS。
      2. 遍历u所有子节点v，并标记这些子节点v已被访问过。
      3. 若是v还有子节点，返回2，否则下一步。
      4. 并查集，把v合并到u上。
      5. 寻找与当前点u有关的询问关系的点v。
      6. 若是v已经被访问过了，则可以确认u和v的最近公共祖先为v所在集合的根节点。

    • 设f[]数组为并查集的父亲节点数组，初始化f[i]=i，vis[]数组为是否访问过的数组，初始为0;

      询问为：LCA(9,8),LCA(4,6),LCA(7,5),LCA(5,3)

    • 图示：

      1. 初始状态：

      2. 以1为根节点DFS，直到节点4访问结束，和4相关的查询有节点6，但6还未访问，说明LCA(4,6)还不确定，把节点4合并到其父节点为根的子树上，即：f[4]=2。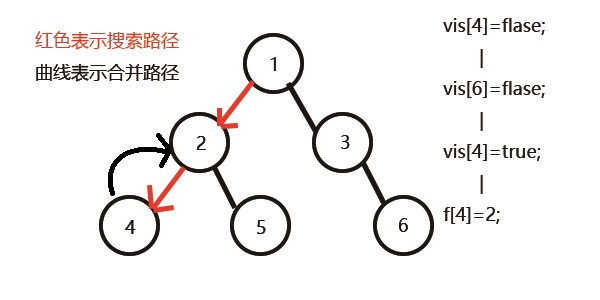

      3. 继续DFS直到搜到节点9结束，和9相关的查询有节点8，但8还未访问，合并9,即：f[9]=7。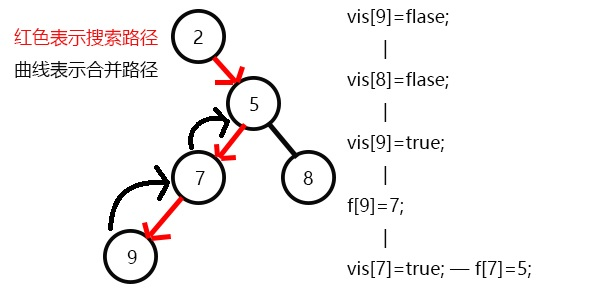

      4. 9结束后回溯到节点7，节点7结束，和7相关的查询有5，此时5虽然没有变黑，但可以肯定5是7的祖先，实际上可以求出LCA(5,7)=5，也可以等5变黑再求均可。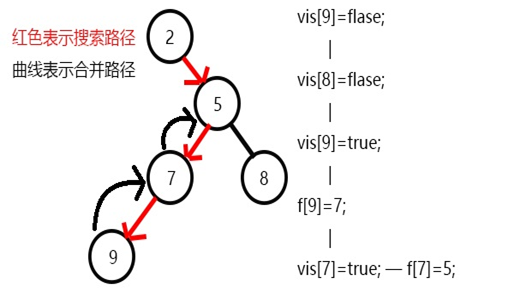

      5. 继续搜8，发现8没有子节点，则寻找与其有关系查询为9，此时9已黑，则他们的最近公共祖先为find(9)=5；在find(9)过程中会把9路径压缩，直接挂到5上，此时因为节点5未变黑，所以f[5]=5，注意父子关系必须变黑后建立

      6. 返回5后，变黑，此时跟5相关的查询点有3和7，3未访问，7已变黑，此时也可以求出LCA(5,7)=find(7)=5。

      7. 回溯到2没有相关查询，一次遍历到节点6，与节点6相关的查询时节点4，且4已黑，在求出LCA(4,6)=1。

      8. 回溯到3,3变黑，和3相关的查询点有5，5已黑，5的祖先节点1即为公共祖先即LCA(3,5)=find(5)=1。

    • 例题：点的距离

      Description

      • 给定一个n个点的树，Q个询问，每次询问x到y点的距离。

      Input

      • 第一行为一个整数n(n<=1e4)，表示n个节点。
      • 接下来n-1行，每行两个整数x,y表示x到y有一条边，所有边权为1。

      Output

      • 输出Q行，表示询问。

      Sample Input

      6
1 2
1 3
2 4
2 5
3 6
2
2 6
5 6

      Sample Output

      3
4

      • code

        #include <bits/stdc++.h>
const int maxn=1e4+5,maxq=1e5+5;
struct Edge{int to,id,next;}e[2*(maxn+maxq)];//询问和树存储在同一个数组
int head[2*maxn],len,n;//1~n存树，n+1~2*n存询问
int dis[maxn],vis[maxn],f[maxn],ans[maxq];//ans[i]存储第i个答案
void Insert(int x,int y,int z){//id记录是第几个询问
	e[++len].to=y;e[len].id=z;e[len].next=head[x];head[x]=len;
}
int Find(int x){
	return x==f[x] ? x : f[x]=Find(f[x]);
}
void Tarjan(int u){
	vis[u]=1;f[u]=u;//初始化并查集
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].to;
		if(vis[v])continue;
		dis[v]=dis[u]+1;//dis[u]表示u到根节点点的距离
		Tarjan(v);
		f[v]=u;//v变黑之后再跟上线建立联系，保证v的子孙节点
	}//在v访问结束之前最远也只能查找到v
	for(int i=head[n+u];i;i=e[i].next){//u变黑，查找u相关的询问
		int v=e[i].to-n,id=e[i].id;
		if(vis[v])//如果v已访问，此时v不一定变黑，有可能为灰此时LCA(u,v)=Find(v)
			ans[id]=dis[u]+dis[v]-2*dis[Find(v)];
	}
}
void Solve(){
	scanf("%d",&n);
	for(int i=1;i<n;++i){
		int u,v;scanf("%d%d",&u,&v);
		Insert(u,v,1);Insert(v,u,1);
	}
	int Q;scanf("%d",&Q);
	for(int i=1;i<=Q;++i){
		int u,v;scanf("%d%d",&u,&v);
		Insert(u+n,v+n,i);Insert(n+v,n+u,i);
	}//询问存储到n+1~2*n
	Tarjan(1);
	for(int i=1;i<=Q;++i)
		printf("%d
",ans[i]);
}
int main(){
	Solve();
	return 0;
}

    • Tarjan 算法需要初始化并查集，所以预处理的时间复杂度为O(n) ，Tarjan 算法处理所有询问的时间复杂度为 O(n+q)。但是 Tarjan 算法的常数比倍增算法大。

    3. 树上倍增求LCA

    • 实现步骤：求LCA(u,v)

      1. DFS求出每个节点相对于根节点的深度d[i]。
      2. 如果d[u]<d[v]，交换节点u和v，如果u和v的深度不一样，找到u的和v在同一深度的祖先节点u'，显然LCA(u,v)==LCA(u',v)。
      3. 如果u'==v，即v正好是u的祖先，则LCA(u,v)=v,结束，否则进行如下操作：
        • 两个点同时向根节点跳 (2^j (j=log(n))) 步，此时有两种可能:
          1. u和v同时跳 (2^j) 步指向同一点，说明他们的 (2^j) 祖先是同一个点，但不一定是最近的公共祖先，有可能跳多了，我们就调小一般的上跳幅度，即跳(2^{j-1})步。
          2. 指向不同的点，此时u,v，我们u和v分别为他们的 (2^j) 祖先。然后减小上跳幅度为原来一半即j--，重复1., 2.，直到j==0，此时两个点必然都在LCA下面那层，所以再跳1步即可。

    • 上面的思想实际上是利用了倍增的思想：

      • 定义：(f[i][j]) 表示节点i往上跳 (2^j) 步后的节点，即i的 (2^j) 祖先 ,显然：

        • (f[i][j]=f[ f[i][j-1] ][j-1])
        • (f[i][0])为i的父亲节点

      • 从根节点进行一遍DFS，可以很快预处理出每个节点的 (2^j) 祖先和深度。

        void dfs(int u,int fa){//对应深搜预处理f数组 
    dep[u]=dep[fa]+1;//预处理节点深度 
    for(int i=1;(1<<i)<=dep[u];i++)
        f[u][i]=f[f[u][i-1]][i-1];//根据u的深度，预处理其2^i祖先 
    for(int i=head[u];i;i=e[i].next){
        int v=e[i].to;
        if(v==fa)continue;
        f[v][0]=u;//v的父亲节点是u 
        dfs(v,u);
    }
}

    • 当u, v不在同一个深度时，我们要用倍增思想把深度大的节点u调到和v在同一个深度。

      int len=dep[u]-dep[v],k=0;
while(len){//对k进行二进制分解
    if(len & 1) u=f[u][k];
    ++k;len>>=1;
}

    • code

      #include<bits/stdc++.h>
const int maxn=1e4+5,maxe=1e5+5;
int n,len,head[maxn],dep[maxn],f[maxn][21];
struct edge{int next,to;}e[2*maxe];
void Insert(int u,int v){
	e[++len].to=v;e[len].next=head[u];head[u]=len;    
}
void dfs(int u,int fa){//对应深搜预处理f数组 
    dep[u]=dep[fa]+1;//预处理节点深度 
    for(int i=1;(1<<i)<=dep[u];i++)
        f[u][i]=f[f[u][i-1]][i-1];//根据u的深度，预处理其2^i祖先 
    for(int i=head[u];i;i=e[i].next){
        int v=e[i].to;
        if(v==fa)continue;
        f[v][0]=u;//v的父亲节点是u 
        dfs(v,u);
    }
}
int lca(int u,int v){
    if(dep[u]<dep[v])std::swap(u,v);
    int len=dep[u]-dep[v],k=0;
    while(len){
    	if(len & 1) u=f[u][k];
    	++k;len>>=1;
	}
	if(u==v)return u;
    for(int i=20;i>=0;i--){//从大到小枚举     
        if(f[u][i]!=f[v][i]){//尽可能接近         
            u=f[u][i];v=f[v][i];
        } 
    } 
    return f[u][0];//u,v在LCA的下一层 
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<n;i++){
        int x,y;scanf("%d%d",&x,&y);
        Insert(x,y);Insert(y,x);
    }
    dfs(1,0);
    int Q;scanf("%d",&Q);
    for(int i=1;i<=Q;i++){
        int u,v;scanf("%d%d",&u,&v);
        printf("%d
",dep[u]+dep[v]-2*dep[lca(u,v)]);//求两个节点的LCA 
    }
}

    • 时间复杂度：倍增算法的预处理时间复杂度为:O(n*log(n)) ，单次查询时间复杂度为 :O(log(n))。

    4. RMQ之ST算法

    • RMQ(Range Minimum/Maximum Query)，即区间最值查询，是指这样一个问题：

      • 对于长度为n的数列A，回答若干询问RMQ(A,i,j)(i,j<=n)，返回数列A中下标在i,j之间的最小/大值。
      • 如果只有一次询问，那样只有一遍for就可以搞定，但是如果有许多次询问就无法在很快的时间处理出来。在这里介绍一个在线算法，ST算法。

    • ST(Sparse Table)算法是一个非常有名的在线处理RMQ问题的算法，它可以在O(nlogn)时间内进行预处理，然后在O(1)时间内回答每个查询。

    • ST算法主要有预处理和查询两种操作：

      1. 预处理

        • (f[i][j]) 表示从i开始的长度为 (2^j) 的一段元素的最小值,则有：

          • (f[i][j]=min(f[i][j-1],f[i+2^{j-1}][j-1]) (2^jle n))

          • 原理如图所示:

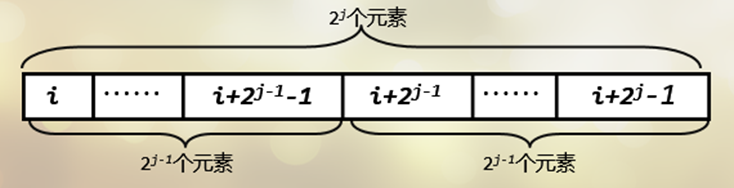
          • code

            void Init(){//ST表初始化
	for(int i=1;i<=n;++i)
		f[i][0]=a[i];
	for(int j=1;(1<<j)<=n;++j)//枚举区间宽度为2^j 
		for(int i=1;i+(1<<j)-1<=n;++i)//枚举区间起点，保证区间终点i+(1<<j)-1<=n 
			f[i][j]=std::max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}

      2. 查询

        • 查询操作很简单,令k为满足 (2^kle R-L+1) 的最大整数,则以L为开头,以R为结尾的两个长度为 (2^k) 的区间合起来即覆盖了区间[L,R].由于是取最值,有些元素重复考虑了几遍也没关系。

        • 原理如图所示：

        • code

          int Ask(int s,int t){//查询区间[s,t]最大值
	int k=log(t-s+1)/log(2);//保证k满足 2^k<r+l-1<=2^(k+1)
	return std::max(f[s][k],f[t-(1<<k)+1][k]);
}

        • 完整代码：

        #include <bits/stdc++.h>
const int maxn=1e4+5;
int n,a[maxn],f[maxn][21];
void Init(){
	for(int i=1;i<=n;++i)
		f[i][0]=a[i];
	for(int j=1;(1<<j)<=n;++j)//枚举区间宽度为2^j 
		for(int i=1;i+(1<<j)-1<=n;++i)//枚举区间起点，保证区间终点i+(1<<j)-1<=n 
			f[i][j]=std::max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
} 
int Ask(int s,int t){
	int k=log(t-s+1)/log(2);//保证k满足 2^k<r+l-1<=2^(k+1)
	return std::max(f[s][k],f[t-(1<<k)+1][k]);
}
void Solve(){
	scanf("%d",&n);//n个点的序列
	for(int i=1;i<=n;++i)
		scanf("%d",&a[i]);
	Init();//st表的初始化
	int Q;scanf("%d",&Q);
	while(Q--){//q个询问
		int x,y;scanf("%d%d",&x,&y);
		printf("%d
",Ask(x,y));
	}
}
int main(){
	Solve();
	return 0;
}

    5. LCA在线做法

    • 算法思想：

      • 从根节点DFS，无论是递归还是回溯，每次到达一个节点就把编号记录下来，得到一个长度为 2N−1 的序列，成为树的欧拉序列 。
      • 由于每条边恰好经过了两次，因此一共记录了2n-1个节点。
      • 用e[1,…,2n-1]来表示这个数组，e[i]表示第i时刻访问的节点编号，并用Firsr[x]来表示节点x第一次被访问的时间。
      • 那么对于任何First[u]<Firts[v]的节点u,v来说，DFS中从第一次访问u到第一次访问v所经过的路径应该是e[First[u],…,First[v]]。
      • 虽然这些节点会包含u的后代，但是其中深度最小的节点一定是u和v的LCA。
      • dep[i]表示节点i的深度，那么当First[u]<=First[v]时，LCA(u,v)=RMQ(dep,First[u],First[v]);
      • 同理，First[u]>First[v]时，LCA(u,v)=RMQ(dep,First[v],First[u]);

    • 图示：

      • 对上图，从节点1开始DFS，很容易得到如下图所示的三个数组：

        • E数组记录图的欧拉序列，下标是时间戳，值是节点编号
        • L数组记录节点的深度序列，下标是时间戳，值是节点到根的深度
        • H数组记录节点的第一次访问时间，下标为节点，值为节点第一次访问时间。

    • code

      #include <bits/stdc++.h>
const int maxn=1e4+5;
struct Edge{
	int to,next;
}a[maxn*2];
int n,e[maxn],f[maxn][21],head[maxn],len;
int Time,dep[maxn],First[maxn],vis[maxn];
void Insert(int x,int y){
	a[++len].to=y;a[len].next=head[x];head[x]=len;
}
void Init(){
	int N=2*n-1;//n个点欧拉序列有2*n-1个时间戳 
	for(int i=1;i<=N;++i)//枚举时间戳 
		f[i][0]=i;//i开始的长度为1的区间里深度最小的时间戳为i 
	for(int j=1;(1<<j)<=N;++j)//枚举区间宽度为2^j 
		for(int i=1;i+(1<<j)-1<=N;++i){//枚举区间起点，保证区间终点i+(1<<j)-1<=n 
			int x=f[i][j-1],y=f[i+(1<<j-1)][j-1];
			if(dep[x]<dep[y])f[i][j]=x;
			else f[i][j]=y;
		}
} 
int Ask(int s,int t){
	int k=log(t-s+1)/log(2);//保证k满足 2^k<r+l-1<=2^(k+1)
	int x=f[s][k],y=f[t-(1<<k)+1][k];
	if(dep[x]<dep[y])return x;
	else return y;
}
int lca(int u,int v){//lca(u,v)在时间戳[First[u],First[v]]区间dep[]最小点
	int x=First[u],y=First[v];
	if(x>y)std::swap(x,y);
	return e[Ask(x,y)];
}
void dfs(int u,int deep){//预处理出节点深度，欧拉序列和节点第一次访问时间
	vis[u]=1;e[++Time]=u;First[u]=Time;dep[Time]=deep;
	for(int i=head[u];i;i=a[i].next){
		int v=a[i].to;
		if(!vis[v]){
			dfs(v,deep+1);
			e[++Time]=u;dep[Time]=deep;
		}
	}
} 
void Solve(){
	scanf("%d",&n);
	for(int i=1;i<n;++i){
		int x,y;scanf("%d%d",&x,&y);
		Insert(x,y);Insert(y,x);
	}
	dfs(1,0);	
	Init();
	int Q;scanf("%d",&Q);
	while(Q--){
		int x,y;scanf("%d%d",&x,&y);
		printf("%d
",lca(x,y));
	}
}
int main(){
	Solve();
	return 0;
}

    • 时间复杂度：预处理的时间复杂度为O(n*log(n)) ，每次查询 LCA 的时间复杂度为O(1) 。
  • 相关阅读:
    pygame--颜色变化
    pyQt绘图
    pyqt布局管理器
    java执行shell/cmd命令
    word公式编辑器公式
    pygame绘制文本
    2.add two number
    eltwise层
    crop层
    fcn
  • 原文地址：https://www.cnblogs.com/hbhszxyb/p/12815765.html
Copyright © 2020-2023  润新知