五、函数

​ C语言的程序是由函数组成的。最简单的程序有一个主函数main()，但实用程序往往由多个函数组成，由主函数调用其他函数，其他函数也可以互相调用。

​ 函数是C语言程序的基本模块，程序的许多功能是通过对函数模块的调用来实现的，学会编写和调用函数可以提高编程效率。

---

5.1 函数的定义

数据类型 函数名(形式参数列表) {
	函数体 //需要执行的语句
}

• 关于函数的定义有如下说明：

1. 函数的数据类型是函数的返回值类型（若数据类型为 void，则无返回值）。函数返回值不能是数组，也不能是函数，除此之外任何合法的数据类型都可以，如：int、long long、float、char等。
2. 函数名是标识符，一个程序中除了主函数名必须为main外，其余函数的名字按照标识符的取名规则可以任意选取，最好取有助于记忆的名字。
3. 形式参数（简称形参）列表可以是空的（即无参函数），也可以有多个形参，形参间用逗号隔开，不管有无参数，函数名后的圆括号都必须有。形参必须有类型说明，形参可以是变量名、数组名或指针名，它的作用是实现主调函数与被调函数之间的关系。
4. 函数中最外层一对花括号“{ }”括起来的若干个语句组成了一个函数的函数体。由函数体内的语句决定该函数功能。函数内部应有自己的说明语句（即变量的定义）和执行语句（即运算），但函数内定义的变量不可以与形参同名，形参和函数内定义的普通变量的生命周期取决于该函数。函数体中也可以没有任何语句，即空函数。
5. 函数不允许嵌套定义。在一个函数内定义另一个函数是非法的。但是允许嵌套使用，也就是后面我们要讲到的递归。
6. 函数在没有被调用的时候是静止的，此时的形参只是一个符号，它标志着在形参出现的位置应该有一个什么类型的数据。函数在被调用时才执行，也就是在被调用时才由主调函数将实际参数（简称实参）值赋予形参。这与数学中的函数概念相似，如数学函数：(f(x)=x^2+x+1)，这样的函数只有当自变量被赋值以后，才能计算出函数的值。

---

5.2 函数定义的例子

//定义一个函数，返回两个数中较大者。
int mymax(int x, int y) {//该函数返回值是整型，有两个整型的形参，用来接受实参传递的两个数据
	return (x > y ? x : y); //函数体内的语句是求两个数中的较大者并将其返回主调函数。
}

5.3 函数的形式

• 函数的形式从结构上说可以分为三种：无参函数、有参函数和空函数。它们的定义形式都相同。

1. 无参函数：无参函数顾名思义即为没有参数传递的函数，无参函数一般不需要带回函数值，所以函数类型说明为void。

2. 有参函数：有参函数即有参数传递的函数，一般需要带回函数值。例如int max(int x,int y)。

3. 空函数：空函数即函数体只有一对花括号，花括号内没有任何语句的函数。例如：

   //空函数不完成什么工作，只占据一个位置。在大型程序设计中，空函数用于扩充函数功能。
   void zhanzuo() {
   }
   

• 编写一个阶乘的函数，我们给此函数取一个名字jc。

  • int jc(int n) {
        int ans = 1;
        for (int i = 1; i <= n; ++i) {
            ans *= i; 
        }
        return ans;
    }
    

  • 在本例中，函数名叫jc，只有一个int型的形参n，函数jc的返回值类型为int。

  • 在本函数中，要用到两个变量i和ans。在函数体中，通过循环结构来求阶乘，n的阶乘的值在ans中，最后由return语句将计算结果ans值返回给主调函数。

  • 函数的形参n是一个接口参数，说得更明确点是入口参数。

  • 如果我们调用函数：js(3)，那么在程序里所有有n的地方，n被替代成3来计算。在这里，3就被称为实参。

  • 如：sqrt(1.44)，abs(-5)，这里4,-5叫实参。而sqrt(double x),abs(int y)中的x,y叫形参。

5.4 函数的声明

• 如果仅仅完成以上内容，我们的程序还不能正常进行，还需要提前告知编译器，我的程序中有一项我自定义的功能，即函数的声明。
• 调用函数之前先要声明函数原型。在主调函数中，或所有函数定义之前，按如下形式声明：

​ 数据类型 函数名(含类型说明的形参表);

• 如果是在所有函数定义之前声明了函数原型，那么该函数原型在本程序文件中任何地方都有效，也就是说在本程序文件中任何地方都可以依照该原型调用相应的函数。

• 如果是在某个主调函数内部声明了被调用函数原型，那么该原型就只能在这个函数内部有效（为了避免麻烦，我们一般不采用这种方式）。

• 下面对jc()函数原型声明是合法的：

  int jc(int n);或int jc(int);

• 可以看到函数原型声明与函数定义时类似，只多了一个分号，少了一对花括号，便成为了一个声明语句。

5.5 函数的调用

• 函数声明了，定义了，剩下的就是使用了，即函数的调用，可以按如下形式调用函数：

​ 函数名 (参数列表)

• 实参列表中应给出与函数原型形参个数相同、类型相符的实参。在主调函数中的参数称为实参，实参一般应具有确定的值。实参可以是常量、表达式，也可以是已有确定值的变量，数组或指针名。函数调用可以作为一条语句，这时函数可以没有返回值。函数调用也可以出现在表达式中，这时就必须有一个明确的返回值。

5.6 函数的返回值

• 在组成函数体的各类语句中，值得注意的是返回语句return。它的一般形式是：return (表达式);
• 其功能是把程序流程从被调函数转向主调函数并把表达式的值带回主调函数，实现函数的返回。
• 圆括号表达式的值实际上就是该函数的返回值。其返回值的类型即为它所在函数的函数类型。
• 当一个函数没有返回值（即void类型）时，函数中可以没有return语句，直接利用函数体的右花括号“}”，作为没有返回值的函数的返回。
• void 类型也可以有return语句，但return后没有表达式。返回语句的另一种形式是：return; 这时函数没有返回值，而只把流程转向主调函数。

---

5.7 我们补全引例的代码

#include<cstdio>
int jc(int); //函数的声明
int main() {
    int sum = 0;
    for (int i = 1; i <= 10; ++i) {
        sum += jc(i); //函数的调用
    }
    printf("sum = %d
", sum);
	return 0;
}
// 函数的定义
int jc(int n) {
    int ans = 1;
    for (int i = 1; i <= n; ++i) {
        ans *= i; 
    }
    return ans; //函数的返回值
}

5.8 递归

5.8.1 概念

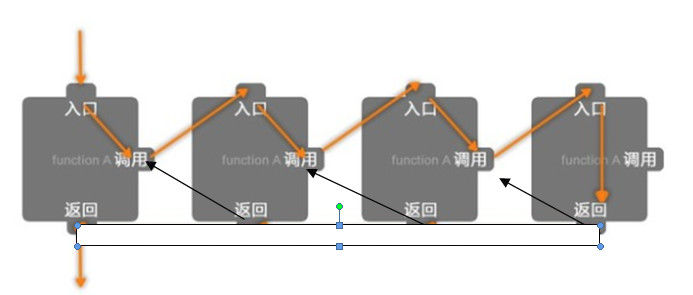
• 递归算法是一种直接或者间接调用自身函数或者方法的算法。

• 递归算法的实质是把问题分解成规模缩小的同类问题的子问题，然后递归调用方法来表示问题的解。它有如下特点：

  • 一个问题的解可以分解为几个子问题的解

  • 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样。

  • 存在递归终止条件，即必须有一个明确的递归结束条件，称之为递归出口，递归出口可能不止一个。

  

5.8.2 例题

5.8.2.1 阶乘

一个正整数的阶乘 factorial是所有小于及等于该数的正整数的积，并且0的阶乘为1，自然数n的阶乘写作 n!。输入正整数n，请求出n!。

• 分析：

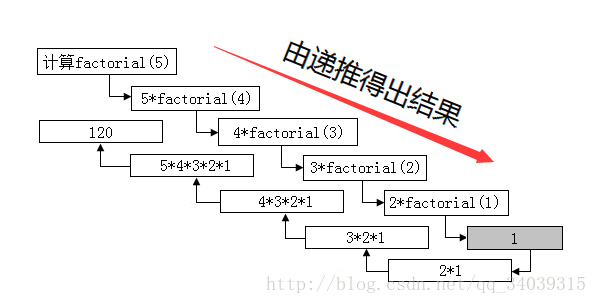
  • 令f(n)表示n的阶乘，如果我们知道f(n-1)的结果，我们即可求出f(n)。
  • f(n-1)的求解过程跟f(n)的求解完全一样，所以我们可以把问题分成规模为1和n-1两个子问题。
  • 递归终止条件：n的规模每次减少1，所以必然会经过f(1)，所以终止条件设为f(1)=1。

• 代码实现：

  int Factorial(int n){
      if(n==1) return 1;//终止条件
      return n*Factorial(n-1);//递归解决n-1问题
  }
  

• 

5.8.2.2 斐波那契数列

斐波那契数列的排列是：0,1,1,2,3,8,13,21,34,55,89,144……依次类推下去，你会发现，它后一个数等于前面两个数的和。在这个数列中的数字，就被称为斐波那契数。输入正整数n，请求出第n项Fibonacci数。

• 分析：

  • 令f(n)表示n的阶乘，很容易得出递推式:f(n)=f(n-1)+f(n-2)。
  • f(n-1)、f(n-2)的求解过程跟f(n)的求解完全一样，所以我们可以把问题分成f(n-1)和f(n-2)两个子问题求解。
  • 递归终止条件：n 的规模每次减少1和2，所以必然会经过f(1)或f(2)，所以终止条件设为f(1)=0,f(2)=1。

• 代码实现：

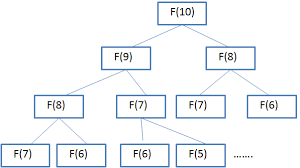
  int Fibonacci(int n){
      if(n==1)return 0;//终止条件1
      if(n==2)return 1;//终止条件2
      return Fibonacci(n-1)+Fibonaci(n-2);
  }
  

• 

• 上图分析发现存在很多的重复计算

  • 比如在计算f(9)的过程中已经计算出了f(8),f(7)...f(3)
  • 求解f(8)的时候所有这些都需要重新计算
  • 如果我们用数组把已经计算过的结果存起来，每次调用的时候如果已经计算过的我们直接使用计算结果，就可以减少大量的冗余计算。
  • 此种方法叫记忆化。

• 记忆化优化代码：

  int Fibonacci(int n){
      if(f[n]>0)return f[n];//如果n已经计算过，直接返回
      if(n==1)return 0;//终止条件1
      if(n==2)return 1;//终止条件2
      return f[n]=Fibonacci(n-1)+Fibonaci(n-2);//返回并记录结果到f[n]
  }
  

5.8.2.3 倒序输出

例如给出n个正整数 {1,2,3,4,5}，希望以各位数的逆序形式输出，即输出{5,4,3,2,1}。希望以递归形式输出。

• 分析：

  • 解决这个问题我们可以倒序输出、也可以建一个栈，先放到栈里，读完再一次输出。
  • 递归是先展开，直到终止的临界条件，再返回，正好像栈，所以递归也可以很好的解决这个问题。

• 代码实现：

  void Reverse(int n){
      if(n==0)return;//终止条件，思考，如果n是任意整数该如何处理？
      int x;
      scanf("%d",&x);
      Reverse(n-1);//递归分解n
      printf("%d ",x);//输出当前的个位数
  }
  

5.8.2.4 汉诺塔

有三根杆子A,B,C。A杆上有n个(n>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：

1. 每次只能移动一个圆盘；
2. 大盘不能叠在小盘上面。

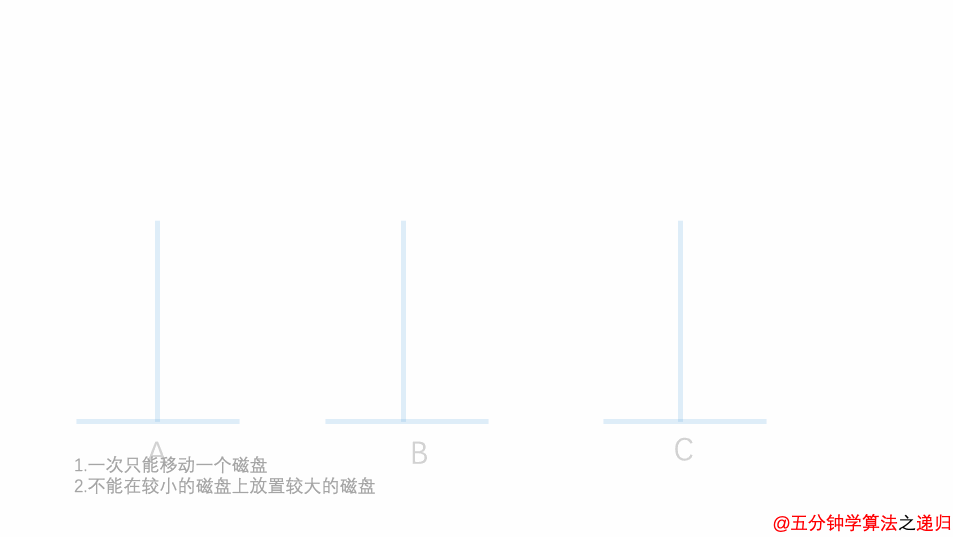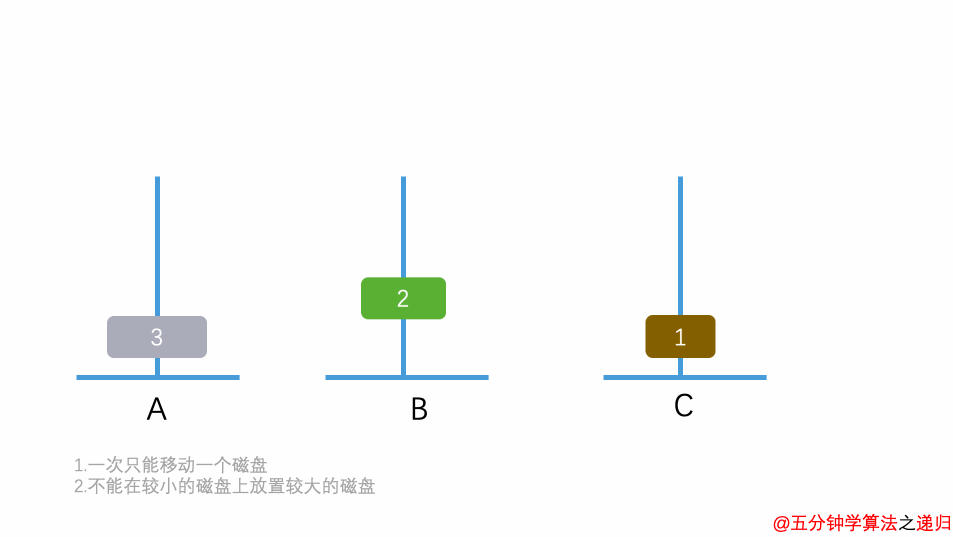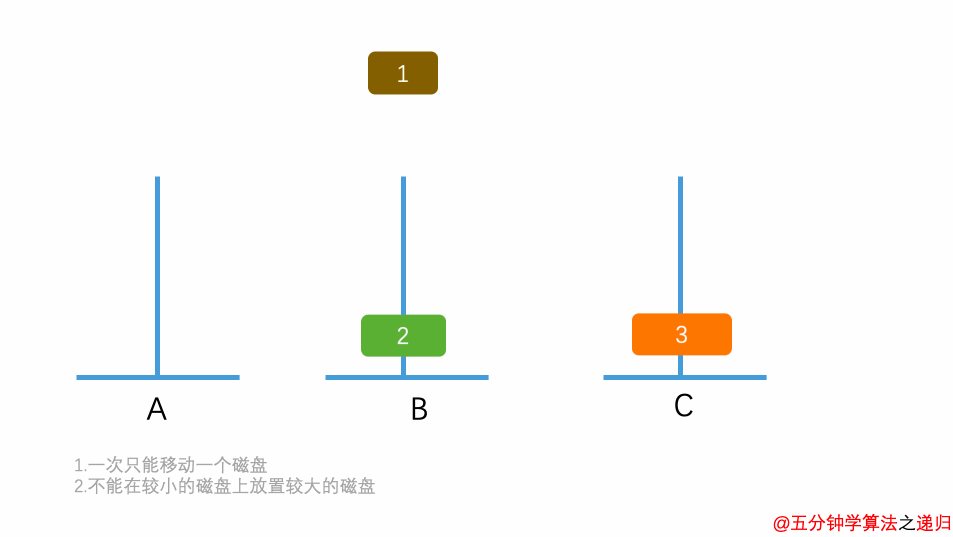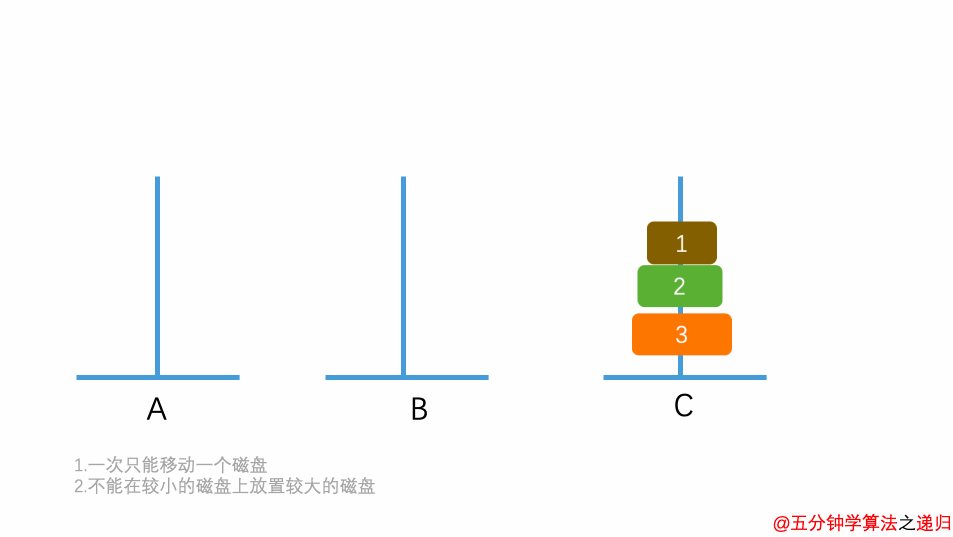
输入正整数n，输出n个盘子的移动过程。

• 分析：

  1. 以C杆为中介，将前n-1个圆盘从A杆挪到B杆上(本身就是一个n-1的汉诺塔问题了！)

  2. 将第n个圆盘移动到C杆上

  3. 以A杆为中介，将B杆上的n-1个圆盘移到C杆上(本身就是一个n-1的汉诺塔问题了！)

     

• 代码实现：

  void Hanoi(int n,char a,char b,char c){
      if(n==1)printf("NO.%d from %c to %c
  ",n,a,c);//只有一个盘子，直接拿过去就行
      else{
          Hanoi(n-1,a,c,b);//先把上面的n-1个盘子通过c移动到b上
          printf("NO.%d from %c to %c
  ",n,a,c);//第n个盘子直接移过去
          hanoi(n-1,b,a,c);//把b柱上的n-1个盘子通过a柱移动到c柱
      }
  }
  

5.8.2.5 二分法

• 分析：

  二分法的一中形式是当 l <= r 的时候再去二分，其中的答案就在某一个区间。对应递归的终止条件的话，即 l > r 的时候就要停止，此时返回我们需要的值，这里以返回 l 为例：

• 代码实现：

  /**
  * a 为查询的数组
  * l 和 r 为确定二分的区间边界
  * key 为要查询的关键字
  */
  int erfen(int a[], int l, int r, int key) {
      if (l > r) return l;	// 终止条件
      int mid = (l + r) >> 1;
      if (a[mid] <= key)
          return erfen(a, mid+1, r, key)
      else
          return erfen(a, l, mid-1, key);
  }
  

5.8.2.5 集合的划分

Description

• 设S是一个具有n个元素的集合，(S＝{a_1,a_2,……,a_n})，现将S划分成k个满足下列条件的子集合$S_1,S_2,…,S_k $，且满足：

  1. (S_i ≠ ∅)
  2. (S_i ∩ S_j ＝ ∅ (1≤i，j≤k i≠j))
  3. (S_1 ∪ S_2 ∪ S_3 ∪ … ∪ S_k ＝ S)

• 则称(S_1,S_2,…,S_k) 是集合S的一个划分。它相当于把S集合中的n个元素(a_1 ,a_2,…,a_n) 放入k个(0＜k≤n＜30)无标号的盒子中，使得没有一个盒子为空。

• 请你确定n个元素(a_1,a_2,…,a_n) 放入k个无标号盒子中去的划分数S(n,k)。

Input

• 给出n和k

Output

• 输出n个元素(a_1 ,a_2,…,a_n) 放入k个无标号盒子中去的划分数S(n,k)。

Sample Input

10 6

Sample Output

22827

• 分析：

  • 设S＝{1,2,3,4},k＝3，不难得出S有6种不同的划分方案，即划分数S(4,3)=6，具体方案为：

    1.{1,2}∪{3}∪{4} 
    2.{1,3}∪{2}∪{4} 
    3.{1,4}∪{2}∪{3} 
    4.{2,3}∪{1}∪{4} 
    5.{2,4}∪{1}∪{3} 
    6.{3,4}∪{1}∪{2} 
    

  • 考虑一般情况，对于任意的含有n个元素(a_1 ,a_2,…,a_n)的集合S，放入k个无标号的盒子中去，划分数为S(n,k)。

  • 我们很难凭直觉和经验计算划分数和枚举划分的所有方案，必须归纳出问题的本质。其实对于任一个元素(a_n)，则必然出现以下两种情况：

    1. ({a_n}) 是k个子集中的一个，于是我们只要把 (a_1,a_2,…,a_{n-1}) 划分为(k－1)子集，便解决了本题，这种情况下的划分数共有(S(n－1,k－1))个；
    2. ({a_n}) 不是(k)个子集中的一个，则 (a_n) 必与其它的元素构成一个子集。
       • 问题相当于先把 (a_1,a_2,…,a_{n-1}) 划分成(k)个子集，这种情况下划分数共有 (S(n－1,k))个；
       • 然后再把元素 (a_n) 加入到k个子集中的任一个中去，共有k种加入方式，这样对于 (a_n) 的每一种加入方式，都可以使集合划分为k个子集，因此根据乘法原理，划分数共有(k * S(n－1,k))个。
    3. 综合上述两种情况，应用加法原理，得出n个元素的集合 ({a_1,a_2,…,a_n}) 划分为k个子集的划分数为以下递归公式：S(n,k)＝S(n－1,k－1) + k * S(n－1,k) (n>k，k>0)。
    4. 记得记忆化哦，(f[s][k]) 表示s个数分成k份的方案数。
    5. 确定S(n,k)的边界条件:
       • 首先不能把n个元素不放进任何一个集合中去，即k=0时，(S(n,k)＝0)；
       • 也不可能在不允许空盒的情况下把n个元素放进多于n的k个集合中去，即k＞n时,S(n，k)＝0；
       • 再者，把n个元素放进一个集合或把n个元素放进n个集合，方案数显然都是1，即k=1或k=n时，S(n,k)=1。

5.8.2.6 放苹果一

Description

• 把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？
• 5,1,1和1,5,1 是同一种分法。

Input

• 第一行是测试数据的数目T(0<=T<=20)。
• 以下每行均包含二个整数M和N，以空格分开。1<=M,N<=10。

Output

• 对输入的每组数据M和N，用一行输出相应的K。

Sample Input

1
7 3

Sample Output

8

• 分析：

  • 此题能否像集合划分一样把m的问题分成m-1和1的问题呢？

  • 我们再来分析一下假设m=4 n=3的情况：共四种:

    1. {1,1} U {1} U {1}
    2. {1,1} U {1,1} U {}
    3. {1,1,1} U {1} U {}
    4. {1,1,1,1} U {} U {}

  • 显然此题不适合用m-1和1的问题，因为允许盘子为空,拿出一个苹果放到哪里都解决不了空的问题

  • 换个思路：我们对盘子进行划分，分成 一个空盘子和 n-1 个装有苹果的盘子。

    • m 个苹果放到 n-1 个盘子里，不许为空正好是个集合的划分，方案数:s(m,n-1) (含义同集合的划分)
    • 但这样并不能解决问题，因为允许空盘子有：0个空盘子,1个空盘子，……,m-1个空盘子
    • 结果为： ans=s(m,n)+s(m,n-1)+…+s(m,1) 。
    • 显然这种思路走不通。

  • 我们重新定义f[m][n]：含义为前n个盘子，放m个苹果，允许为空的方案数。

    • 我们尝试是否把当前模型转换成我们熟悉的模型，显然，允许盘子为空的方案数包含了不许盘子为空。

      • m个苹果放到n 个盘子里，不许为空，显然是一个集合划分问题，方案数为：s(m,n) 。

      • 去掉不为空的方案数，剩下的显然是m个苹果放到n-1 个盘子里，允许为空 。方案数：f[m][n-1]

      • 所以递推式：f[m][n]=f[m][n-1]+s(m,n) 。

        • f[m][n] 和 S(m,n) 数据规模一样，并没有减少，是无法递归出结果的。

        • S(m,n) 表示没有空盘子，那我们对每个盘子拿走一个苹果，并不影响方案数。

          • 每个盘子拿走一个苹果后盘子的情况是什么呢？

            1. 每个盘子都有苹果
            2. 有可能若干个空盘子

          • 天！这不就是m-n个苹果放在n个盘子里，可以为空的方案数吗？？即：s(m,n)=f[m-n][n]

          • 强大吧？？开始膜拜吧！！：）

      • 最终递推式：f[m][n]=f[m][n-1] + f[m-n][n] 。

      • 临界条件：

        1. m==1 || n==1：显然只有一个苹果或只有一个盘子，方案必然是1
        2. m<n：如果苹果比盘子少，那多出来的盘子怎么都是空，所以：f[m][n]==f[m][m] ,即让n=m。
        3. m==0：显然m-n的过程中必然会出现m==0，没有苹果时应该也是一种方案，即f[0][]=1。

5.8.2.7 放苹果二

Description

• 把M个同样的苹果放在N个同样的盘子里，不允许有的盘子空着不放，问共有多少种不同的分法？
• 5,1,1和1,5,1 是同一种分法。

Input

• 第一行是测试数据的数目T(0<=T<=20)。
• 以下每行均包含二个整数M和N，以空格分开。1<=M,N<=10。

Output

• 对输入的每组数据M和N，用一行输出相应的K。

Sample Input

1
7 3

Sample Output

4

• 分析：
  • 此题貌似和集合的划分 类似，不同的地方是，每一个苹果都是相同的，而集合的划分里每个元素各不相同
  • 如果我们跟集合划分 一样把问题分成两个子问题：
    1. 1个苹果放在一个盘子，剩下的n-1个苹果放在k-1个盘子
    2. n-1个苹果放在k个盘子，然后剩下的一个苹果在这k个盘子选一个放。
  • 因为每个苹果都一样，我们无法处理重复的分发
    • 例如：7 个苹果放在3 个盘子，我们先拿出一个苹果，剩下的6个苹果每个盘子放两个，之后这一个苹果无论放在哪个盘子里，都是同一种方案。
    • 如果剩下的6个苹果三个盘子分别放：1个，2个，3个，那剩下的一个苹果放在不同的盘子是不同的方案，所以方案数为3
  • 换个思路，f(n,k)表示n个苹果放在k个盘子，不许为空的方案，我们把问题分成下面两个子问题：
    1. 至少一个盘子里有一个苹果
       • 拿出一个苹果，那剩下的就是n-1个苹果放在k-1个盘子，不许为空的方案数，正好是递归的子问题
       • 方案数为：f(n-1,k-1)
    2. 没有一个盘子里只有一个苹果，即盘子里的苹果数至少为2
       • 我们可以先在k个盘子里均放一个苹果，那么还剩下n-k个苹果
       • 剩下的n-k个苹果放在k个盘子里，不许为空。正好保证每个盘子苹果数为2个和2以上。
    3. 递推式：f(n,k)=f(n-1,k-1) + f(n-k,k)

5.8.2.8 整数划分

Description

• (n=m_1+m_2+...+m_i) ; （其中(m_i)为正整数，并且(1 <= m_i <= n)），则({m_1,m_2,...,m_i})为n的一个划分。
• 如果({m_1,m_2,...,m_i})中的最大值不超过(m)，即(max(m_1,m_2,...,m_i)<=m)，则称它属于(n)的一个(m)划分。这里我们记(n)的(m)划分的个数为(f(n,m));

Input

• 第一行是测试数据的数目T(0<=T<=20)。
• 以下每行均包含二个整数n和m，以空格分开。1<=n,m<=10。

Output

• 对输入的每组数据n和m，输出整数划分的方案数。

Sample Input

1
4 3

Sample Output

4

• 分析：

  • n=4,m=3可分为如下几种情况:

    1. 4=3+1
    2. 4=2+2
    3. 4=2+1+1
    4. 4=1+1+1+1

  • 我们把上面的情况都用1的集合表示：

    1. {1,1,1},{1}
    2. {1,1},{1,1}
    3. {1,1},{1},{1}
    4. {1},{1},{1},{1}

  • 通过上面的分析，貌似，好像跟分苹果有点类似恶，不过分苹果是对分的份数有限制，而整数划分随便你分多少份（貌似最多也只能分n份），但对每一份的个数有限制。

  • 解决此问题我们需要解决以下几个问题：

    1. 如何缩小问题的规模
    2. 如何解决解决数的大小的限制
    3. 临界条件的处理

  • 根据n和m的关系，考虑以下几种情况：

    1. 当n=1时，不论m的值为多少（m>0)，只有一种划分即是{1}
    2. 当m=1时，不论n的值为多少，只有一种划分即n个1，{1,1,1,...,1}
    3. 当n==m时，根据划分中是否包含n，可以分为两种情况：
       • 划分中包含n的情况，只有一个即{n}；
       • 划分中不包含n的情况，这时划分中最大的数字也一定比n小，即n的所有(n-1)划分。因此 f(n,n) =1 + f(n,n-1);
    4. 当n<m时，由于划分中不可能出现负数，因此就相当于f(n,n);
    5. 但n>m时，根据划分中是否包含最大值m，可以分为两种情况：
       • 划分中包含m的情况，即({m, {x_1,x_2,...x_i}}), 其中${x_1,x_2,... x_i} (的和为)n-m(，可能再次出现)m$，因此是(n-m)的m划分，因此这种划分个数为f(n-m, m);
       • 划分中不包含m的情况，则划分中所有值都比m小，即n的(m-1)划分，个数为f(n,m-1);因此 f(n, m) = f(n-m, m)+f(n,m-1);
    6. 综合以上情况，我们可以看出，上面的结论具有递归定义特征，其中 1 和 2 属于回归条件，3 和 4 属于特殊情况，将会转换为情况 5。而情况 5 为通用情况，属于递推的方法，其本质主要是通过减小 m 以达到回归条件，从而解决问题。
    7. 分析到最后貌似结果跟分苹果是一样的啊,那请大家分析一下,这两个问题是不是一样的?请证明.

• 可能从题面上看,《整数划分》和《分苹果》的方案数是一样的。比如：n=10，k=4，我们让10个苹果放在4个盘子，不允许空我们可以用如下图来表示:

  

• 把上图的三个矩形顺时针旋转90度后

  

• 从上面的图形分析上，我们可以看出如果把n分成k个数之和的每一个方案都跟把n分成若干份之和，且最大数为k的方案一一对应，那么如果我们允许盘子为空和最大值不大于k正好一一对应，所以分苹果和整数划分一样！

• 这个问题告诉我们分析问题不要只看表象，一定要分析问题实质

例题总结：

• 上面的四个例题实际上只有两个模型,第一题《集合划分》是一个模型,此模型的特点是每个元素是唯一的，所以我们把n个不同的元素分成k个部分，不允许为空，我们可以把一个元素拿出来，这个元素可以是单独组成一个集合，也可以和其他元素组成集合所以递推式是：f(n,k)=f(n-1,k-1)+f(n-1,k)*k。请思考，如果允许集合为空我们该怎么处理？
• 后面的三个问题，《分苹果》、《数的划分》、《整数划分》实际上可以认为是一个模型，我们认为每个集合里的数只是代表个数，他们都是由相同的1构成的，比如3，我们可以认为是3个相同的1构成，n是那个相同的1构成。所以我们认为是相同的n个元素不同的组合。
• 《分苹果》和《数的划分》实际上是一个问题，我们可以这样认为分苹果是把n个相同的1分成k份，但允许一份的最小个数0，数的划分我们可以认为把n分成k份，每一份最小为1。

例题扩展：

1. 整数划分中，(n=m_1+m_2+...+m_i) ，每个数最多只允许使用一次时的方案数？

   • 分析：
     • 此问题是在整数划分的基础上增加了一重限制，即，(m_1,m_2,...,m_i) i 个元素互不相同。
     • 整数划分的通用递推公式为：f(n,m)=f(n,m-1)+f(n-m,m)
       • f(n,m-1)：表示方案中累加因子里没有m，最大可能为m-1的方案数，显然是一个递归的子问题。
       • f(n-m,m)：表示方案中累加的因子里有m，剩下的因子之和为n-m的方案数。
         • 关键问题是，剩下的因子里有没有可能存在m的问题。
         • f(n-m,m) 表示最大因子不超过m，如果n-m>=m，是可能分出等于m的因子的。
         • 那如何让剩下的因子不能为m呢？
         • 显然我们只需修改最大限制即可，即把m编成m-1，即f(n-m,m)修改成 f(n-m,m-1).
     • 递推公式为：f(n,m)=f(n,m-1)+f(n-m,m-1)

2. 整数划分中，(n=m_1+m_2+...+m_i) ，要求(m_1,m_2,...,m_i) 均为奇数的方案数。

   • 方法一：
     • 定义f[i][j]：正整数i划分成 j 个奇正整数之和的方案数。
     • 义g[i][j]：正整数i划分成 j 个偶正整数之和的方案数。
     • 问题分成两个子问题：
       1. 方案中包含至少一个奇数1
          • 从i中拿出一个1，则剩下的i-1分出j-1 个奇数之和
          • 正好是一个递归的子问题
          • 方案数为：f[i-1][j-1]
       2. 方案中没有奇数1，即最小的奇数至少为3
          • 从i中拿出j个1 放到每一份中。
          • 剩下的i-j，我们只需分成j个偶数即可
          • 方案数为：g[i-j][j]
     • 递推公式：f[i][j]=f[i-1][j-1] + g[i-j][j]
     • 临界条件：
       1. 当i<j时：f[i][j]=0, g[i][j]=0
       2. 当i==j时：
   • 方法二：
     • 设f[n][k]表示n的划分中最大值为k的划分数。
       1. 当 k = 1 时，其结果只能为n个1。
       2. 当 k 是偶数时，有f[n][k] == f[n][k-1]。
       3. 当 k > n 时，有f[n][k] = f[n][n] 。
       4. 当 n >= k 时，我们可以把问题分为两个子问题：
          1. 方案中有奇数k，拿出奇数k,剩下的n-k，分出不超过k的方案数：f[n-k][k]。
          2. 方案中没有奇数k，则方案数为f[n][k-1],因为k为奇数，可以直接写上f[n][k-2]。

五种模型代码实现：

//1.将n划分成若干正整数之和的划分数,结果对Mod取余。
int Part1(int n,int m){//把n分成最大因子不超过m的划分，若干相当于m==n
    if(f[n][m])return f[n][m];//记忆化
    if(n==1||m==1||n==0)return f[n][m]=1;//临界
    if(n<m)return f[n][m]=Part1(n,n)%Mod;//没有负数，最大因子不可能大于n
    return f[n][m]=(Part1(n-m,m)%Mod+Part1(n,m-1)%Mod)%Mod;//方案中有m和没有m进行递归解决
}
//2.将n划分成k个正整数之和的划分数，结果对Mod取余。
int Part2(int n,int k){
    if(f[n][k])return f[n][k];//记忆化
    if(k==1||n==k)return f[n][k]=1;//临界
    if(n<k)return 0;//n不可能划分出大于n份的正整数之和
    return f[n][k]=(Part2(n-1,k-1)%Mod+Part2(n-k,k)%Mod)%Mod;//方案中有1和没有1进行递归解决
}
//3.将n划分成最大数不超过k的划分数,结果对Mod取余。
//同Part1
//4.将n划分成若干个奇正整数之和的划分数,结果对Mod取余。
int Part4(int n,int k){//把n分成最大因子不超过k的划分
    if(f[n][k])return f[n][k];//记忆化
    if(k==1||n==0)return f[n][k]=1;//临界
    if(n<k)return f[n][k]=Part4(n,n)%Mod;//分出的因子最大不可能超过n
    if(k%2==0)return f[n][k]=Part4(n,k-1)%Mod;//k为偶数，显然最大因子为k-1
    if(k%2==1)return f[n][k]=(Part4(n-k,k)%Mod+Part4(n,k-1)%Mod)%Mod;//k为奇数，分成有k和没有k递归处理
}
//5.将n划分成若干不同整数之和的划分数,结果对Mod取余。
int Part5(int n,int k){//n分成最大因子不超过k，且最多为一个的划分
    if(f[n][k])return f[n][k];//记忆化
    if(k==1&&n>1)return 0;//最多只能有一个1
    if(n==1||n==0||k==1)return f[n][k]=1;//临界
    if(n<k)return f[n][k]=Part5(n,n)%Mod;//最大因子不可能超过n
    return f[n][k]=(Part5(n-k,k-1)%Mod+Part5(n,k-1)%Mod)%Mod;//方案中有k其递归子问题最大不能超过k-1
}