Problem 1 射命丸文(aya.cpp/c/pas)
题目描述 在幻想乡,射命丸文是以偷拍闻名的鸦天狗。当然,文文的照相机可不止能够照相,还能够消除取景框里面所有的弹幕。假设现在文文面前有一块N行M列的弹幕群,每一个单位面积内有分值有num[i][j]的弹幕。相机的取景框可以将一块R行C列的弹幕消除,并且得到这一块区域内所有弹幕的分值(累加)。现在文文想要取得尽可能多的分值,请你计算出她最多能够得到的分值。
输入格式 第1行:4个正整数N,M,R,C
第2..N+1行:每行M个正整数,第i+1行第j个数表示num[i][j]
输出格式 第1行:1个整数,表示文文能够取得的最大得分
输入样例 3 5 2 3
5 2 7 1 1
5 9 5 1 5
3 5 1 5 3
输出样例 33
数据范围 对于60%的数据:1 <= N,M <= 200
对于100%的数据:1 <= N,M <= 1,000
1 <= R <= N, 1 <= C <= M
1 <= num[i][j] <= 1000
保证结果不超过2,000,000,000
Problem 2 帕秋莉•诺蕾姬(patchouli.cpp/c/pas)
题目描述 在幻想乡,帕秋莉•诺蕾姬是以宅在图书馆闻名的魔法使。这一天帕秋莉又在考虑如何加强魔法咒语的威力。帕秋莉的魔法咒语是一个仅有大写字母组成的字符串,我们考虑从’A’到’Z’分别表示0到25的数字,于是这个魔法咒语就可以看作一个26进制数。帕秋莉通过研究发现,如果一个魔法咒语所代表的数能够整除10进制数M的话,就能够发挥最大的威力。若当前的魔法咒语并不能整除M,帕秋莉只会将其中两个字符的位置交换,尽量让它能够被M整除,当然由于某些咒语比较特殊,无论怎么改变都不能达到这个目的。请你计算出她能否只交换两个字符就让当前咒语被M整除。(首位的’A’为前导0)
输入格式 第1行:1个字符串,长度不超过L。
第2行:1个正整数,M
输出格式 第1行:用空格隔开的2个整数,输出时先输位置靠前的那个。
如果存在多种交换方法,输出字典序最小的,比如1 3和1 5都可以达到目的,就输出1 3;1 3和2 4都行时也输出1 3。注意字符串下标从左到右依次为1到L开始。如果初始魔法咒语已经能够整除M,输出”0 0”;若无论如何也不能到达目的输出”-1 -1”。
输入样例 PATCHOULI
16
输出样例 4 9
数据范围 对于30%的数据:1 <= L <= 10, 1 <= M <= 100
对于50%的数据:除前面30%外,1 <= L <= 500, M = 5或25或26
对于100%的数据:1 <= L <= 2,000, 1 <= M <= 200,000
Problem 3 雾雨魔理沙(marisa.cpp/c/pas)
题目描述 在幻想乡,雾雨魔理沙是住在魔法之森普通的黑魔法少女。话说最近魔理沙从香霖堂拿到了升级过后的的迷你八卦炉,她迫不及待地希望试试八卦炉的威力。在一个二维平面上有许多毛玉(一种飞行生物,可以视为点),每个毛玉具有两个属性,分值value和倍率mul。八卦炉发射出的魔法炮是一条无限长的直线形区域,可以视为两条倾斜角为α的平行线之间的区域,平行线之间的距离可以为任意值,如下图所示:
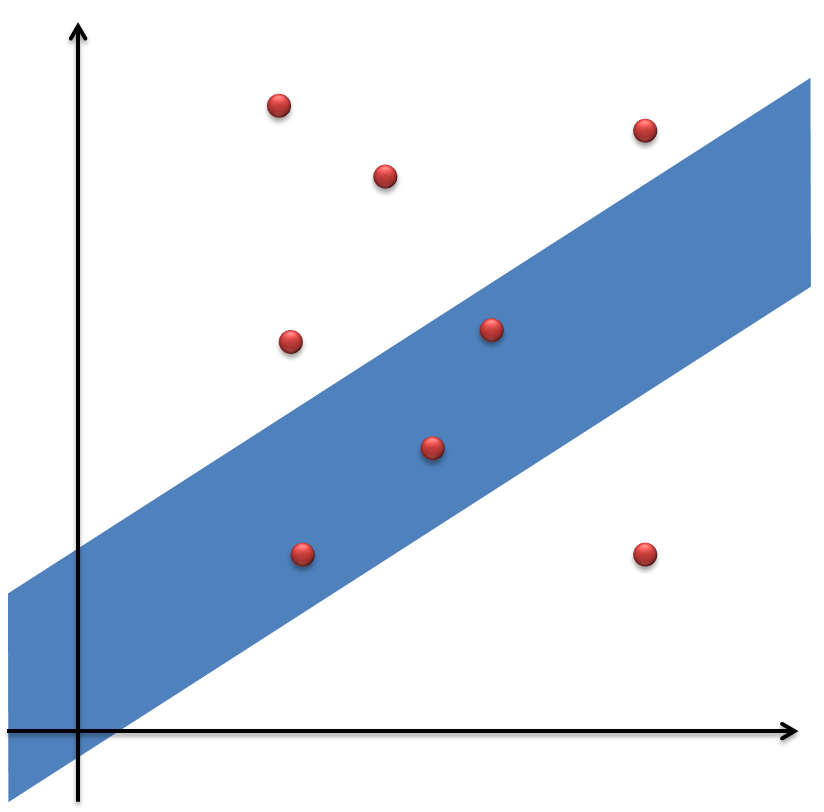
蓝色部分上下两条长边之间就是这次八卦炉的攻击范围,在蓝色范围内的毛玉(红点)属于该此被击中的毛玉,如果一个毛玉刚好在边界上也视为被击中。毛玉击中以后就会消失,每次发射八卦炉得到分值是该次击中毛玉的分值和乘上这些毛玉平均的倍率,设该次击中的毛玉集合为S,则分值计算公式为:
Score = SUM{value[i] | i 属于 S} * SUM{mul[i] | i 属于 S} / |S|
其中|S|表示S的元素个数。魔理沙将会使用若干次八卦炉,直到把所有毛玉全部击中。任意两次攻击的范围均不重叠。最后得到的分值为每次攻击分值之和。现在请你计算出能够得到的最大分值。
输入格式 第1行:1个整数N,表示毛玉个数
第2..N+1行:每行四个整数x, y, value, mul,表示星星的坐标(x,y),以及value和mul
第N+2行:1个整数α,表示倾斜角角度,0°到180°
输出格式 第1行:1个实数,表示最大分值,保留三位小数
输入样例 3
1 3 3 1
2 1 2 2
3 4 2 1
45
输出样例 9.333
数据范围 对于60%的数据:1 <= N <= 500
对于100%的数据:1 <= N <= 2,000
-10,000 <= x,y <= 10,000
1 <= value,mul <= 100
注意 π = 3.1415926
Problem 4 伊吹萃香(suika.cpp/c/pas)
题目描述 在幻想乡,伊吹萃香是能够控制物体密度的鬼王。因为能够控制密度,所以萃香能够制造白洞和黑洞,并可以随时改变它们。某一天萃香闲着无聊,在妖怪之山上设置了一些白洞或黑洞,由于引力的影响,给妖怪们带来了很大的麻烦。于是他们决定找出一条消耗体力最少的路,来方便进出。已知妖怪之山上有N个路口(编号1..N),每个路口都被萃香设置了一定质量白洞或者黑洞。原本在各个路口之间有M条单向路,走过每一条路需要消耗一定量的体力以及1个单位的时间。由于白洞和黑洞的存在,走过每条路需要消耗的体力也就产生了变化,假设一条道路两端路口黑白洞的质量差为delta:
1. 从有白洞的路口走向有黑洞的路口,消耗的体力值减少delta,若该条路径消耗的体力值变为负数的话,取为0。
2. 从有黑洞的路口走向有白洞的路口,消耗的体力值增加delta。
3. 如果路口两端均为白洞或黑洞,消耗的体力值无变化。
由于光是放置黑洞白洞不足以体现萃香的强大,所以她决定每过1个单位时间,就把所有路口的白洞改成黑洞,黑洞改成白洞。当然在走的过程中你可以选择在一个路口上停留1个单位的时间,如果当前路口为白洞,则不消耗体力,否则消耗s[i]的体力。现在请你计算从路口1走到路口N最小的体力消耗。保证一定存在道路从路口1到路口N。
输入格式 第1行:2个正整数N, M
第2行:N个整数,第i个数为0表示第i个路口开始时为白洞,1表示黑洞
第3行:N个整数,第i个数表示第i个路口设置的白洞或黑洞的质量w[i]
第4行:N个整数,第i个数表示在第i个路口停留消耗的体力s[i]
第5..M+4行:每行3个整数,u, v, k,表示在没有影响的情况下,从路口u走到路口v需要消耗k的体力。
输出格式 第1行:1个整数,表示消耗的最小体力
输入样例 4 5
1 0 1 0
10 10 100 10
5 20 15 10
1 2 30
2 3 40
1 3 20
1 4 200
3 4 200
输出样例 130
数据范围 对于30%的数据:1 <= N <= 100, 1 <= M <= 500
对于60%的数据:1 <= N <= 1,000, 1 <= M <= 5,000
对于100%的数据:1 <= N <= 5,000, 1 <= M <= 30,000
其中20%的数据为1 <= N <= 3000的链
1 <= u,v <= N, 1 <= k,w[i],s[i] <= 200
样例说明 按照1 -> 3 -> 4的路线。
Aya 射命丸文
题目大意 对于给定的N*M的矩形,在其中找一个R*C的权值最大的区域
考察算法 模拟 枚举
算法一 以每一个格子为左上角枚举R*C的区域,并求出它的权值之和。最后取其中的最大值。此算法包含4重循环。
时间复杂度:O(N^4) 期望得分:60
算法二 我们设S[i,j]表示以(i,j)为右下角,(1,1)为左上角的区域的权值之和,那么我们以(i,j)为右下角的R*C的区域权值之和的计算公式为:
Area[i,j]=S[i,j]+S[i-R,j-C]-S[i-R,j]-S[i,j-C]
其中S[i,j]的计算公式为:
S[i,j]=value[i,j]+S[i-1,j]+S[i,j-1]-S[i-1,j-1]
你可以随手画图出来,很容易即可证明上面两个式子。最后取Area[]中的最大值即可。
时间复杂度:O(N^2) 期望得分:100
#include <iostream> #include <cstdio> using namespace std; #define MAXN 2048 int value[ MAXN ][ MAXN ]; int N, M, R, C; int main() { int sum, Max = 0; scanf("%d %d %d %d", &N, &M, &R, &C); for (int i = 1; i <= N; i++) for (int j = 1; j <= M; j++) { scanf("%d", &value[i][j]); value[i][j] += value[i - 1][j] + value[i][j - 1] - value[i - 1][j - 1]; } for (int i = R; i <= N; i++) for (int j = C; j <= M; j++) { sum = value[i][j] - value[i - R][j] - value[i][j - C] + value[i - R][j - C]; if (sum > Max) Max = sum; } printf("%d\n", Max); return 0; }
Patchouli 帕秋莉•诺蕾姬
题目大意 对于给定的字符串,转化为26进制数字,交换其中两个字母的位置,使得这个数字能被M整除
考察算法 字符串 进制转换 同余问题
算法一 对于30%数据,可以转换成一个10进制数,并且这个10进制数是小于2^63-1的。枚举每一对字母进行交换,若当前字符串所对应的10进制数能够整除M,输出即可。当所有情况都试过仍然不可行,则无解。
时间复杂度:O(N^2*L) 期望得分:30
算法二 在算法一的基础上加上对5,25,26的特判:对于5,25只要各位数字之和能够被5或25整除,则该数能够5或25整除,否则无解;对于26,只需判断字符串内是否有’A’,无’A’则无解,否则只需把’A’换至最后一位,就能被26整除。
时间复杂度:O(N^2*L) 期望得分:50
算法三 建立新的数组v[],v[i]=26^(i-1) mod M,将v[1..L]作为右数第1..L位的新权值,最后计算每一位的数字与它对应的新权值之积的和,即:
Sum = SUM{ num[i]*v[i] | 1 <= i <= N }
如果Sum能够整除M,则原26进制能够整除M。剩下的事就是枚举每一对字母进行交换,再进行判断。交换可以用O(1)的时间实现,公式如下:
NewSum = Sum–num[i]*v[i]-num[j]*v[j]+num[i]*v[j]+num[j]*v[i]
证明也很简单,这里就不多讲了。
时间复杂度:O(N^2) 期望得分:100
#include <iostream> #include <cstdio> using namespace std; #define MAXL 1024 char str[ MAXL ]; int fir[ MAXL ], rest[ MAXL ]; int L, MOD; int main() { scanf("%s", str); scanf("%d", &MOD); L = 0; for (int i = 0; str[i]; i++) fir[++L] = str[i] - 'A'; long long tp, sum = 0; rest[L] = 1, sum = fir[L]; for (int i = L - 1; i >= 1; i--) { rest[i] = (rest[i + 1] * 26) % MOD; sum += rest[i] * fir[i]; } if (sum % MOD == 0) printf("0 0\n"); else { int x, y, ans_x, ans_y; bool flag = false; for (x = 1; x < L && !flag; x++) for (y = x + 1; y <= L && !flag; y++) { tp = sum - rest[x] * fir[x] - rest[y] * fir[y]; tp += rest[x] * fir[y] + rest[y] * fir[x]; if (tp % MOD == 0) { ans_x = x, ans_y = y; flag = true; } } if (!flag) ans_x = ans_y = -1; printf("%d %d\n", ans_x, ans_y); } return 0; }
Marisa 雾雨魔理沙
题目大意 平面上有若干个带权点,用倾斜角为α的直线将其分为若干部分,每部分可以得到一个分值,求一个最大得分。
考察算法 解析几何 动态规划
算法一 对于α为0或90度的情况进行特判,分别按照y坐标或x坐标排序,然后进行动态规划,DP方程如下:
f[i]=Max{f[j]+SUM{value[k]|j<k<=i}*SUM{mul[k]|j<k<=i}/(i-j)}
值的注意的一点是,如果两个点进行排序的坐标相同,则这两个点始终是属于同一个区域,不能被分开。在枚举j的时候需要特判一下。
时间复杂度:O(N^2) 期望得分:20
算法二
由上图我们可以看出,当斜率为任意值时,仍然可以对当前节点进行排序。此时我们计算出过每个点的斜角为α的直线与y轴的交点,并按照这个交点的y坐标d进行排序。其计算公式为:
d = y – k * x
之后同样按照算法一的DP方程进行动态规划。同样需要注意那些必然在一个区域内的点。
时间复杂度:O(N^2) 期望得分:100
#include <algorithm> #include <iostream> #include <vector> #include <cstdio> #include <cmath> using namespace std; #define MAXN 2048 #define Pi 3.1415926 vector< pair<int, int> > cde; vector< pair<double, int> > order; int N; double f[ MAXN ], value[ MAXN ], mul[ MAXN ], k; double val[ MAXN ], m[ MAXN ]; int a; bool Compare(pair<double, int> elem1, pair<double, int> elem2) { return elem1.first > elem2.first; } int main() { scanf("%d", &N); double x, y; for (int i = 1; i <= N; i++) { scanf("%lf %lf %lf %lf", &x, &y, &value[i], &mul[i]); cde.push_back( make_pair(x, y) ); } scanf("%d", &a); if (a != 90) { k = tan(double(a) * Pi / 180); for (int i = 0; i != cde.size(); i++) order.push_back( make_pair(cde[i].second - k * cde[i].first, i + 1) ); } else for (int i = 0; i != cde.size(); i++) order.push_back( make_pair(cde[i].first, i + 1) ); sort(order.begin(), order.end(), Compare); for (int i = 0; i != order.size(); i++) { val[i + 1] = value[ order[i].second ]; m[i + 1] = mul[ order[i].second ]; if (i) val[i + 1] += val[i], m[i + 1] += m[i]; } for (int i = 1; i <= N; i++) { f[i] = val[i] * m[i] / i; for (int j = 1; j < i && order[j - 1].first != order[i - 1].first; j++) if (f[i] < f[j] + (val[i] - val[j]) * (m[i] - m[j]) / (i - j) ) f[i] = f[j] + (val[i] - val[j]) * (m[i] - m[j]) / (i - j); } printf("%.3lf\n", f[N]); return 0; }
Suika 伊吹萃香
题目大意 给定一张有向图,通过一条边时间为1,代价为边权,奇偶时刻边权不同,可以停留于某一点,代价s[i]。求从节点1到节点N的最小代价。
考察算法 最短路
算法一 对于链状的数据,可以使用贪心法解决。每个时刻只有两种决策,要么移动到下一个点,要么等颜色变换后再移动。可以分别求出两种决策的代价,选择代价较少的一种。
时间复杂度:O(N) 期望得分:20
算法二 本题实际上是简化的分层图最短路,可将原图中的点集拆为颜色相反的两部分,分别代表奇时刻和偶时刻,不同时刻之间再相互连边,最后使用最短路算法解决即可。
时间复杂度:O(N^2)/O(NlogN)/O(KM) 期望得分:100
算法三 由于题目中图的结构不会随时间改变,所以拆点时并不需要将边集一并拆开,只需在dist数组中加上时间维即可。对于SPFA算法O(KM)的时间复杂度,易知减少边数能在很大程度上节约时空开支,此方法在分层图层数较多时尤其适用。
时间复杂度:O(KM) 期望得分:100
#include <iostream> #include <cstdio> #include <vector> #include <queue> using namespace std; #define MAXN 10009 #define Inf 999999999 #define abs(x) (x > 0 ? x : -(x)) struct EDGE { int v, w; }; vector<EDGE> fir[ MAXN ]; queue<int> q; int w[ MAXN ], s[ MAXN ], pro[ MAXN ]; int dist[ MAXN ]; bool vis[ MAXN ]; int N, M; void Addedge(int rt, int s, int k) { EDGE tp = {s, k}; fir[rt].push_back(tp); return ; } void InputGraph() { int u, v, k, delta; scanf("%d %d", &N, &M); for (int i = 1; i <= N; i++) scanf("%d", &pro[i]); for (int i = 1; i <= N; i++) scanf("%d", &w[i]); for (int i = 1; i <= N; i++) scanf("%d", &s[i]); for (int i = 1; i <= N; i++) { Addedge(i * 2, i * 2 - 1, 0); Addedge(i * 2 - 1, i * 2, s[i]); } while (M--) { scanf("%d %d %d", &u, &v, &k); if (pro[u] == pro[v]) { Addedge(u * 2 - 1, v * 2, k); Addedge(u * 2, v * 2 - 1, k); } else { delta = abs(w[u] - w[v]); Addedge(u * 2 - 1, v * 2 - 1, k + delta); Addedge(u * 2, v * 2, k - delta > 0 ? k - delta : 0); } } } int SPFA(int start) { int NN, tp; NN = N << 1; for (int i = 1; i <= NN; i++) dist[i] = Inf; dist[ start ] = 0; q.push( start ); vis[ q.front() ] = true; while (q.size()) { tp = q.front(); vis[tp] = false; q.pop(); for (int i = 0; i != fir[tp].size(); i++) if (dist[ fir[tp][i].v ] > dist[tp] + fir[tp][i].w) { dist[ fir[tp][i].v ] = dist[tp] + fir[tp][i].w; if (!vis[ fir[tp][i].v ]) { vis[ fir[tp][i].v ] = true; q.push( fir[tp][i].v ); } } } return dist[N * 2] < dist[ N * 2 - 1 ] ? dist[N * 2] : dist[ N * 2 - 1 ]; } int main() { InputGraph(); printf("%d\n", SPFA(pro[1] ? 1 : 2)); return 0; }
壮哉我SPFA!!!
另:除了上面的算法外,不排除还有其他更优的解法。