链接
https://ac.nowcoder.com/acm/contest/5673/I
题意
给n对数,从上到下开始取数
每一对有三种操作
1)两个都不选
2)如果a没选过,可以选a
3)如果b没选过,可以选b
问最多可以选多少个数
思路
先说解法:
对每行的两个数字连边,建图
统计图中有多少棵树,点的总数cnt减去树的棵树tot即为答案
再说证明:
对于此题有一个技巧,对于一对数,我们可以用一条无向边将他们连起来,比如a-b,如果我们要选择a,就给这条边加上方向a<-b
现在考虑一组数据:
1 2
1 3
2 4
2 5
很明显根据最优解建出的图应该是:
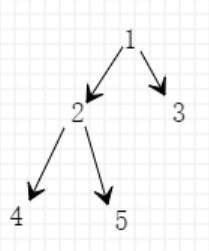
可以发现对于树的根,它是不在解里的
对于其他样例也是同样的道理
回到技巧的说明中,我们选择一个点而放弃另一个点,等于给一个点的入度变为0,如果在之后的选择中我们选择了这个点,这个点的入度就增加了,也就是说对于这个图,所有入度为0的点就是被抛弃的点
考虑不是树的情况,也就是图存在环,根据上面所说,没有点被抛弃
所以我们的做法是建图->找出所有的树->统计
具体的操作有很多种,比如我们可以对图中的连通块进行遍历,如果连通块中无环,那么连通块对答案的贡献为大小减1,否则贡献就是连通块的大小
而判环和统计连通块的大小就很简单了,dfs并查集,这里贴上我校dalao的bfs做法(其实我没看懂(能跑就行
代码
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define ms(a) memset(a, 0, sizeof(a))
#define repu(i, a, b) for (int i = a; i < b; i++)
#define repd(i, a, b) for (int i = a; i > b; i--)
using namespace std;
typedef long long ll;
typedef long double ld;
const int M = int(1e5)*3 + 5;
const int mod = int(1e9) + 7;
struct edge {
int to;
int w;
int next;
};
edge edges[M * 60];
int head[M * 5];
int cnt;
void add(int u, int v, int w) {
edges[cnt].to = v;
edges[cnt].w = w;
edges[cnt].next = head[u];
head[u] = cnt++;
edges[cnt].to = u;
edges[cnt].w = w;
edges[cnt].next = head[v];
head[v] = cnt++;
}
void init() {
cnt = 0;
memset(head, -1, sizeof(head));
}
map<int, int> m;
int ans = 0;
bool vis[M];
int top[M];
int bfs(int s) {
if (vis[s]) return 0;
queue<int> q;
top[s]=0;
q.push(s);
bool cir = 0;
bool dcir = 0;
int cnt = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
if (vis[u]) continue;
vis[u] = 1;
dcir=0;
for (int i = head[u]; ~i; i = edges[i].next) {
int v = edges[i].to;
if (vis[v] == 1) {
if (top[u] == v && dcir == 0) {
dcir = 1;
} else {
cir = 1;
}
continue;
}
q.push(v);
top[v] = u;
}
cnt++;
}
return cnt - 1 + cir;
}
void solve() {
init();
m.clear();
ans = 0;
ms(vis);
ms(top);
int n;
cin >> n;
int tot = 0;
repu(i, 0, n) {
int x, y;
cin >> x >> y;
if (m.find(x) == m.end()) {
m[x] = ++tot;
}
if (m.find(y) == m.end()) {
m[y] = ++tot;
}
// cout<<m[x]<<" "<<m[y]<<endl;
add(m[x], m[y], 1);
}
repu(i, 1, tot+1) { ans += bfs(i); }
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T;
cin >> T;
repu(t, 1, T + 1) {
solve();
cout << "Case #" << t << ": " << ans << endl;
}
return 0;
}