多项式模板

多项式乘法

多项式表示方法

以下的多项式长度为(n)，即最高次数为(n-1)，共(0,1,cdots n-1)，(n)位多项式

系数表示法

即最常见的表示方法：

[f(x)=a_0+a_1x+a_2x^2+cdots a_{n-1}x^{n-1}=sumlimits_{i=0}^{n-1}a_ix^i ]

存储时只存每一位的系数即可

[f(x)={a_0,a_1,a_2,cdots,a_{n-1}} ]

点值表示法

即把多项式放到平面直角坐标系内，得到一个函数图像

把(n)个不同的(x)带入，得到(n)个(y)

[f(x)={(x_0,f(x_0)),(x_1,f(x_1)),(x_2,f(x_2)),cdots,(x_{n-1},f(x_{n-1}))} ]

系数表示法是最常见的一种表示法，而点值表示法是最方便的一种表示法

系数表示法的方便之处不用多说，简单说一下点值表示法的好处：

计算多项式乘法时：点值表示法可以(O(n))求，即对应每一位乘起来即可

[f(x) cdot g(x)={(x_0,f(x_0)g(x_0),(x_1,f(x_1)g(x_1),cdots (x_{n-1},f(x_{n-1})g(x_{n-1})} ]

这两种表示法可以相互转化。但是暴力转化的话，系数转点值是(O(n^2))的

那么就需要用到下面的两种办法来解决一下，把时间优化到(O(nlog n))

快速傅里叶变换 FFT

上面说过，对于任意系数多项式转点值，当然可以随便取任意(n)个(x)值代入计算，但是时间为(O(n^2))

那么考虑找一些(x)值使得(x^n=1)，这样(n)次方后就会出现循环，就不用做全部的(n)次方运算了

但是这样的(x)只有(pm 1)，那么需要考虑把它弄到复数域去

复数

定义(i^2=-1)，用(z=a+bi)表示复数。(a)称为实部，(b)称为虚部。(z'=a-bi)称为(z)的共轭复数（即虚部取反）

运算法则（(z_1=a+bi,z_2=c+di)）：

[z_1+z_2=(a+c)+(b+d)i ]
[z_1cdot z_2=(ac-bd)+(ad+bc)i ]

struct Complex{double a,b;Complex(double xx=0,double yy=0){a=xx,b=yy;}}
inline Complex operator+(Complex x,Complex y){x.a+=y.a;x.b+=y.b;return x;}
inline Complex operator-(Complex x,Complex y){x.a-=y.a;x.b-=y.b;return x;}
inline Complex operator*(Complex x,Complex y){return Complex(x.a*y.a-x.b*y.b,x.a*y.b+x.b*y.a);}

回到正题

有一个(x)轴为实部，(y)轴为虚部的坐标轴。作一个以原点为圆心，(1)为半径的单位圆

使得(x^n=1)的(x)一定在这个圆上，即把这个圆(n)等分，得到的交点。理解一下：把这个角度乘上(n)倍一定与(x)轴正方向重合

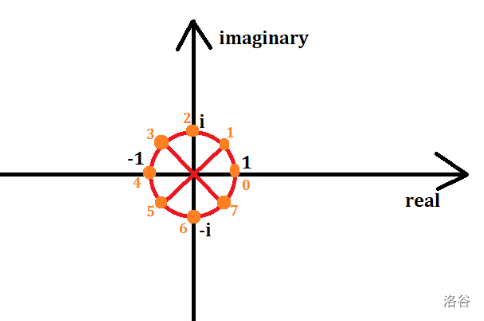
设这个交点为$ omega_n^{k$（分成$n$份，$omega_n$的$k$次方），$omega_n}k$为单位根

[omega_n^k=cos frac{k}{n}2pi+sinfrac{k}{n}2picdot i ]

结合这个图理解一下

单位根的性质

[omega_n^k=omega_{2n}^{2k}=omega_{mn}^{mk} ]

直接带定义式即可证明

[omega_n^{k+frac{n}{2}}=-omega_n^k ]
[omega_n^0=omega_n^n=1 ]

终于到了FFT的时间

[f(x)=(a_0+a_2x^2+cdots+a_{n-2}x^{n-2})+x(a_1+a_3x^2+cdots x_{n-1}x^{n-2}) ]

令(f_1(x)=a_0+a_2x+a_4x^2+cdots+a_{n-2}^{frac{n}{2}-1}),(f_2(x)=a_1+a_3x+a_5x^2+cdots+a_{n-1}^{frac{n}{2}-1})

则(f(x)=f_1(x)+xf_2(x))

带入(omega_n^k)得

[f(omega_n^k)=f_1(omega_n^{2k})+omega_n^kf_2(omega_n^{2k})=f_1(omega_frac{n}{2}^k)+omega_n^kf_2(omega_frac{n}{2}^k) ]

带入(omega_n^{k+frac{n}{2}}=-omega_n^k)得

[f(omega_n^{k+frac{n}{2}})=f_1(omega_n^{2k})-omega_n^kf_2(omega_n^{2k})=f_1(omega_frac{n}{2}^k)-omega_n^kf_2(omega_frac{n}{2}^k) ]

所以求出(f(omega_n^k))的同时可以求出(f(omega_n^{k+frac{n}{2}}))，把一个(n)优化到了(log n)

注意FFT必须令多项式的长度为(2)的整数次方，否则多加几位0使它等于(2)的整数次方位

while(len<=n+m)len<<=1,++cnt;

递归求解即可

但是递归的常数巨大，考虑直接把每个数直接交换到相应的位置上

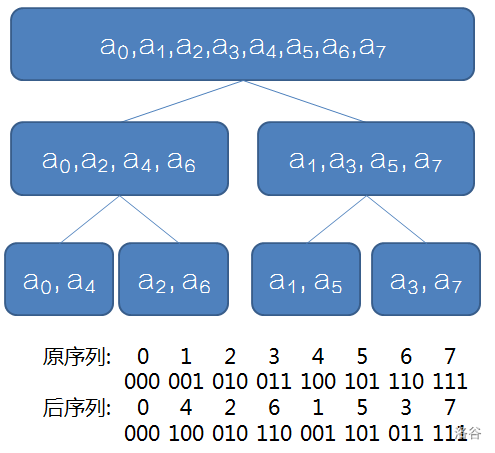
可以发现：交换后序列的位置为交换前序列的二进制下翻转过来

for(int i=0;i<len;++i)	pos[i]=(pos[i>>1]>>1)|((i&1)<<(cnt-1));

解释一下这个的含义：把自己的最后一位去掉（i>>1），翻转（pos[i>>1]>>1，即去掉自己的最后一位反转的结果多了一位(0)，把这个(0)去掉），再把最后一位弄上去（((i&1)<<(cnt-1))）

再结合一个例子：已知(00101)翻转为(10100)，再求(01011)翻转后的值

去掉最后一位（第一位补(0)）：(00101)，翻转(10100)，去掉最后一位(01010)，原来的最后一位补上去(11010)

得到了应该放到的位置后交换：

for(int i=0;i<len;++i)if(i<pos[i])swap(f[i],f[pos[i]]);

这个if必须要有，不然要来回交换两次，相当于没动

inline void FFT(Complex *f){
	for(int i=0;i<len;++i)	if(i<pos[i])swap(f[i],f[pos[i]]);
	for(int mid=1;mid<len;mid<<=1){
		Complex base=Complex(cos(Pi/mid),sin(Pi/mid));
		for(int j=0;j<len;j+=(mid<<1)){
			w=Complex(1,0);
			for(int k=j;k<j+mid;++k,w=w*base){
				Complex x=f[k],y=w*f[k+mid];
				f[k]=x+y;f[k+mid]=x-y;
			}
		}	
	}
}

至此我们完成了 系数表示法转点值表示法

IFFT（快速傅里叶逆变换）

现在我们需要完成 点值表示法转系数表示法

把(omega_n^k)换成其的共轭复数，再对其系数都除以(len)（(len)为(2^k)）

证明如下：

(omega_n^k)的共轭复数=(omega_n^{-k})，根据三角函数的性质可以得到(cos(-x)=cos x,sin(-x)=-sin x)，带回单位根的定义式即可

现在我们已经得到了一个函数(f(x))在(omega_n^0,omega_n^1,cdots,omega_n^{n-1})的点值(g(x))，设为(y_0,y_1,cdots,y_{n-1})，求出原函数(f(x))的各项系数(f_0,f_1,cdots,f_{n-1})

[g(x)=sumlimits_{i=0}^{n-1}y_ix^i,y_i=sumlimits_{j=0}^{n-1}f_j(omega_n^i)^j ]

代入得

[g(x)=sumlimits_{i=0}^{n-1}sumlimits_{j=0}^{n-1}f_j(omega_n^i)^jx^i ]

把(omega_n^{-k})作为(x)代入

[g(x)=sumlimits_{i=0}^{n-1}sumlimits_{j=0}^{n-1}f_j(omega_n^i)^{j-k}=sumlimits_{j=0}^{n-1}f_jsumlimits_{i=0}^{n-1}(omega_n^{j-k})^i ]

令(S(x)=sumlimits_{i=0}^{n-1}(omega_n^{x})^i)，则有(omega_n^x S(x)=sumlimits_{i=0}^{n-1}(omega_n^{x})^i)

两式相减得

[S(x)=dfrac{(omega_n^x)^n-(omega_n^x)^0}{omega_n^x-1}=dfrac{(omega_n^n)^x-1}{omega_n^x-1}=dfrac{1-1}{omega_n^x-1}=dfrac{0}{omega_n^x-1} ]

当(omega_n^x=1(x<n))时，即(x=0)时，(S(0)=sum_{i=0}^{n-1}1^i=n)，否则该式(=0)

带回原式

[g(omega_n^{-k})=sumlimits_{j=0}^{n-1}f_jS(j-k) ]

当(j=k)时(S(j-k)=n)，其余时候(S(j-k)=0)

那么

[g(omega_n^{-k})=nf_j ]

所以对当前已知点值表示法的(g(x))代入(omega_n^{-k})，再除以(n)，即可得到系数表示法的(f(x))

inline void FFT(Complex *f,int flag){
	for(int i=0;i<len;++i)	if(i<pos[i])swap(f[i],f[pos[i]]);
	for(int mid=1;mid<len;mid<<=1){
		Complex base=Complex(cos(Pi/mid),flag*sin(Pi/mid));//取-1即为点值转系数
		for(int j=0;j<len;j+=(mid<<1)){
			w=Complex(1,0);
			for(int k=j;k<j+mid;++k,w=w*base){
				Complex x=f[k],y=w*f[k+mid];
				f[k]=x+y;f[k+mid]=x-y;
			}
		}	
	}
}

主函数中

while(len<=n+m)	len<<=1,++cnt;
for(int i=0;i<len;++i)	pos[i]=(pos[i>>1]>>1)|((i&1)<<(cnt-1));
FFT(a,1);FFT(b,1);
for(int i=0;i<len;++i)	a[i]=a[i]*b[i];
FFT(a,-1);
for(int i=0;i<=n+m;++i)printf("%.0lf ",(a[i].a+0.5)/len);//注意精度

快速数论变换 NTT

FFT的精度会爆炸（(sin,cos)当然了），我们需要一种精度更高的做法

阶

若(a,p)互素，且(p>1)，

对于(a^n≡1pmod p)最小的(n)，我们称之为(a)模(p)的阶,记做(δ_p(a))

例如：(δ_7(2)=3)

原根

设(p)是正整数，(a)是整数，若(δ_p(a))等于(ϕ(p))，则称(a)为模(p)的一个原根，记为(g)

(δ_7(3)=6=ϕ(7))，因此(3)是模(7)的一个原根

注意原根的是不唯一的

于是可以得到一个结论

[omega_nequiv g^frac{p-1}{n} pmod p ]

用这个可以代替FFT中的单位根(omega)，因为它满足FFT中虚数(omega)的全部性质（模意义下）

证明（以下等号均表示在(mod p)意义下同余）：

性质(1)：(omega_n^0=omega_n^n=1)

显然 (omega_n^0=g^0=1)，(omega_n^n=g^{p-1})

根据费马小定理(g^{p-1}equiv 1 pmod{p})，得证

性质(2)：(omega_{2n}^{2k}=omega_n^k)

直接代定义式得：(omega_{2n}^{2k}=(g^{frac{p-1}{2n}})^{2k}=g^{frac{2kcdot(p-1)}{2n}}=g^{frac{kcdot(p-1)}{n}}=(g^{frac{p-1}{n}})^k=omega_n^k)

性质(3)：(omega_{n}^{k+frac{n}{2}}=-omega_n^k)

[(omega_n^{frac{n}{2}})^2=g^{p-1}equiv1pmod p ]

[omega_n^{frac{n}{2}}equivpm1pmod p ]

补充一条原根的性质：

若(P)为素数，那么原根(g^imod p) ((forall i in (0,P)cap N_{ast}))的结果两两不同

那么(omega_n^{frac{n}{2}} e omega_n^{n},omega_n^n=1)，那么(omega_n^{frac{n}{2}}equiv -1 pmod p)

那么(omega_n^{k+frac{n}{2}}=omega_n^kcdotomega_n^{frac{n}{2}}=-omega_n^k)，得证

即把FFT中的(omega_n^k=cos frac{k}{n}2pi+sinfrac{k}{n}2picdot i)替换为 (g^{k imesfrac{p-1}{n}}mod p)即可

原根没什么快速求法，只能暴力枚举判断
通常模数常见的有(998244353 , 1004535809,469762049)。这几个的原根都是(3)

还原的话取(g^{-frac{p-1}{n}})，即(inv(g)^frac{p-1}{n})即可

顺便加上封装，代码如下

const int mod=998244353,G=3,N=(1<<21)+10;
namespace Math{
	int inv[N],pos[N],curmx;
	inline int add(int a,int b){return (a+b>=mod)?a+b-mod:a+b;}
	inline int dec(int a,int b){return (a-b<0)?a-b+mod:a-b;}
	inline int mul(int a,int b){return 1ll*a*b%mod;}
	inline int quick_pow(int a,int b){int ret=1;for(;b;b>>=1,a=mul(a,a))if(b&1)ret=mul(a,ret);return ret;}
	inline int Inv(int a){return quick_pow(a,mod-2);}
	int invg=Inv(G);
	inline int init_pos(int n){
		int len=1,cnt=0;while(len<=n)len<<=1,++cnt;
		for(int i=0;i<len;i++)pos[i]=(pos[i>>1]>>1)|((i&1)<<(cnt-1));
		return len;
	}
}
using namespace Math;
struct poly{
	vector<int> v;
	inline int& operator[](int a){while(a>=v.size())v.push_back(0);return v[a];}//取第x位，若不足则补0
	inline void clear(int a,int b){for(int i=a;i<b;++i)v[i]=0;}
}f,g;
namespace Basic{
	inline void Read(int n,poly &f){for(int i=0;i<n;++i)f[i]=read();}//读入
	inline void Print(int n,poly f){for(int i=0;i<n;++i)printf("%d ",f[i]);puts("");}//输出
	inline void cpy(int n,poly &f,poly f1){for(int i=0;i<n;++i)f[i]=f1[i];}
	inline void NTT(poly &f,int len,int flag){
		for(int i=0;i<len;i++)if(i<pos[i])swap(f[i],f[pos[i]]);
		for(int mid=1;mid<len;mid<<=1){
			int base=quick_pow((flag==1)?G:invg,(mod-1)/(mid<<1));
			for(int i=0,w=1;i<len;i+=(mid<<1),w=1)
				for(int j=i;j<i+mid;++j,w=mul(w,base)){
					int x=f[j],y=mul(w,f[j+mid]);
                    f[j]=add(x,y),f[j+mid]=dec(x,y);
				}
		}
	}
	inline void Mul(poly &a,poly b,int n,int m){
		int len=init_pos(n+m);init_inv(len);
		NTT(a,len,1);NTT(b,len,1);for(int i=0;i<len;++i)a[i]=mul(a[i],b[i]);
		NTT(a,len,-1);int invn=inv[len];
		for(int i=0;i<len;i++)a[i]=mul(a[i],invn);//还原
	}
}
using namespace Basic;
int n,m;
int main(){
	n=read()+1;m=read()+1;
	Read(n,f);Read(m,g);
	Mul(f,g,n,m);Print(n+m-1,f);
	return 0;
}

其余的相关计算多项式运算

多项式乘法逆

已知(f(x))，求(g(x))使得(f(x)cdot g(x)equiv1pmod{x^n})

考虑递归求解

假设我们已经求出(h(x))，使得(h(x)cdot f(x)equiv1pmod{x^{leftlceilfrac{n}{2} ight ceil}})，现在要求(g(x)cdot f(x)equiv1pmod{x^n})

那么显然(g(x)cdot f(x)equiv 1 pmod{x^{leftlceilfrac{n}{2} ight ceil}})

两式相减得

[f(x)cdot(h(x)-g(x))equiv 0 pmod{x^{leftlceilfrac{n}{2} ight ceil}} ]

即

[h(x)-g(x)equiv 0 pmod{x^{leftlceilfrac{n}{2} ight ceil}} ]

两边平方得

[h(x)^2-2h(x)g(x)+g(x)^2equiv 0 pmod{x} ]

两边同时乘以(f(x))

[f(x)cdot h(x)^2-2f(x)h(x)g(x)+f(x)cdot g(x)^2equiv 0 pmod{x} ]

根据(f(x)g(x)equiv 1 pmod{x})

[f(x)cdot h(x)^2-2h(x)+g(x)equiv 0pmod{x} ]

移项得结论：

[g(x)equiv 2h(x)-f(x)h(x)^2 ]

边界条件：(n=1)时，(g(0)cdot f(0)equiv1pmod x)，取(g(0)=inv(f(0)))

直接NTT即可

注意代码的一些细节

(g(x))在(mod x^n) 意义下，所以次数(ge n)的位系数均为(0)
代入公式时，先把(h(x),f(x))NTT一遍得到点值表示，直接进行乘、减运算，这样得到的仍然是一个点值表示，再NTT一遍转回系数表示

poly Get_inv(poly f,int n){//求逆 
	poly g;
	if(n==1){g[0]=Inv(f[0]);return g;}
	g=Get_inv(f,(n+1)>>1);
	int len=init_pos(n<<1);
	poly a;cpy(n,a,f);
	NTT(a,len,1);NTT(g,len,1);
	for(int i=0;i<len;++i)g[i]=mul(dec(2,mul(a[i],g[i])),g[i]);
	NTT(g,len,-1);int invn=Inv(len);
	for(int i=0;i<len;++i)g[i]=(i<n)?mul(g[i],invn):0;
	return g;
}

多项式对数函数（多项式ln）

已知多项式(A(x))，求(B(x))使得(B(x)equiv ln A(x)pmod{x^n})

保证(a_0=1)

前置芝士：

求导

大概就是求函数上某个点的斜率，用(f'(x))表示(f(x))的导函数，用(f^{(i)})表示(f(x))的(i)阶导

常用公式

[(u(x)pm v(x))'=u'(x)pm v'(x) ]

[(u(x)cdot v(x))'=u'(x)v(x)+u(x)+v'(x) ]

[left(dfrac{u(x)}{v(x)} ight) '=dfrac{u'(x)v(x)-v'(x)u(x)}{v^2(x)} ]

同时这三个公式都可以推广到(n)个

[(x^n)'=nx^{n-1} ]

那么结合上述两个公式可以得到

对于(f(x))求导，即对每一位求导再加起来。(f(x))的第(i)次：(f_ix^i)求导得(if_ix^{i-1})

那么(f'(x)=sumlimits_{i=1}^{n-1}if_ix^{i-1})，(f'(x))的第(n-1)次项系数为(0)

代码

inline poly derive(poly f,int n){
	poly ret;
    for(int i=1;i<n;++i)ret[i-1]=mul(f[i],i);
    return ret;
}//求导

复合函数求导

(y(x)=f(g(x)))，则

[y'(x)=f'(g(x))cdot g'(x) ]

特殊函数求导

[(ln x)'=dfrac{1}{x} ]

积分

即求导的逆运算

inline poly interg(poly f,int n){
	poly ret;
    for(int i=1;i<n;++i)ret[i]=mul(f[i-1],Inv(i));
    return ret;
}//积分

回到正题

令(f(x)=ln x)，则

[B(x)equiv f(A(x))pmod{x^n} ]

两边求导得

[B'(x)equiv f'(A(x))A'(x)pmod{x^n} ]

根据((ln x)'=dfrac{1}{x})

[B'(x)equiv dfrac{A'(x)}{A(x)}pmod{x^n} ]

然后积分积回去即可

[B(x)equivintdfrac{A'(x)}{A(x)} ]

inline poly Get_ln(poly f,int n){//对数函数 
	poly der=derive(f,n);//求导
   	poly g=Mul(der,Get_inv(f,n),n,n);//除法（乘上逆）
	return interg(g,n);//积回去
}

多项式牛顿迭代

前置芝士

泰勒展开

将一个在(x=x_0)处具有(n)阶导数的函数(f(x))利用关于((x-x_0))的(n)次多项式来逼近函数

当然这个(n)越大，函数就越逼近

成立下式：

[f(x)=sumlimits_{i=0}^{infty}dfrac{f^{(i)}(x_0)}{i!}(x-x_0)^i ]

其中(f^{(i)})表示(f(i))的(i)阶导

已知(f(x))，求(g(x))使(f(g(x))equiv 0pmod{n^n})

类似倍增

假设已经求出了(g_0(x))满足(f(g_0(x))equiv 0pmod{x^{leftlceilfrac{n}{2} ight ceil}})

在(g_0(x))处进行泰勒展开

[f(g_0(x))=sumlimits_{i=0}^{infty}dfrac{f^{(i)}(g_0(x))}{i!}(g(x)-g_0(x))^i ]

因为(f(g(x))equiv 0pmod{n^n})，(f(g_0(x))equiv 0pmod{x^{leftlceilfrac{n}{2} ight ceil}})

那么(g_0(x))和(g(x))的最后(leftlceilfrac{n}{2} ight ceil)位必须相同

即

[g(x)-g_0(x)equiv 0pmod {x^{leftlceilfrac{n}{2} ight ceil}} ]

那么(forall ige 2)

[g(x)-g_0(x)equiv 0pmod x ]

那么上面的泰勒展开式中(ige 2)的((g(x)-g_0(x))^i)都为(0)，也就是说只有(i=0,1)的两项

把这两项展开得

[f(g(x))equiv f(g_0(x))+f'(g_0(x))(f(x)-g_0(x))pmod{x^n} ]

移项

[f'(g_0(x))g(x)+f(g_0(x))-f'(g_0(x))g_0(x)equiv 0 pmod {x^n} ]

[g(x)equiv g_0(x)-dfrac{f(g_0(x))}{f'(g_0(x))} pmod {x^n} ]

(n=1)时需要特判边界

这样往下迭代即可

多项式指数函数（多项式 exp）

已知(f(x))，求(g(x))满足(g(x)equiv e^{f(x)}pmod{x^n})

保证(a_0=0)

两边取(ln)得

[ln g(x)equiv f(x)pmod{x^n} ]

[ln g(x)-f(x)equiv 0pmod{x^n} ]

代入刚才的牛顿迭代式

[g(x)equiv g_0(x)-dfrac{ln g_0(x)-f(x)}{frac{1}{g_0(x)}}pmod{x^n} ]

[equiv g_0(x)(1-ln g_0(x)+f(x))pmod{x^n} ]

递归即可

边界（(n=1)）：因为题目保证(f(x))常数项为(0)，那么(ln g(x)=0)，即(g(x)=1)

poly Get_exp(poly f,int n){//指数函数 
	poly g;if(n==1){g[0]=1;return g;}
	g=Get_exp(f,(n+1)>>1),n;poly a=Get_ln(g,n);
	for(int i=0;i<n;i++)a[i]=add((i==0),dec(f[i],a[i]));
	return Mul(g,a,n,n);
}

多项式除法

已知(n-1)次多项式(f(x))和一个(m-1)次多项式(g(x))，求多项式(Q(x)),(R(x))

(Q(x))为商，(R(x))为余数
(Q(x))次数为(n-m)，(R(x))次数小于(m-1)（暂且令其为(m-2)次）

只要我们把(Q(x))找出来了，那么(f(x)-g(x)Q(x))即可得到(R(x))

设(h_r(x))表示翻转(h(x))的各项系数后的函数

inline void rev(poly &f,int n){reverse(f.v.begin(),f.v.begin()+n);}

这个满足(h_r(x)=x^{n-1}h(dfrac1x))

来推式子（下面式子除说明外，(=)表示(mod x^n)意义下相等）

[f(x)=Q(x)cdot g(x)+r(x) ]

[f(frac1x)=Q(frac1x)cdot g(frac1x)+r(frac1x) ]

两边同时乘上(x^{n-1})

[x^{n-1}f(frac1x)=x^{n-m}Q(frac1x)cdot x^{m-1}g(frac1x)+x^{n-m+1}cdot x^{m-2}R(frac1x) ]

这里的次数分配有助于下一步化简

转换为(h_r)形式

[f_r(x)equiv Q_r(x)cdot g_r(x)+x^{n-m+1}R_r(x)pmod{x^{n-m+1}} ]

[f_r(x)equiv Q_r(x)cdot g_r(x)pmod{x^{n-m+1}} ]

[Q_r(x)equiv f_r(x)cdot g_r^{-1}(x)pmod{x^{n-m+1}} ]

求出(g_r(x))的逆，再乘上(f_r(x))即可得到(Q_r(x))。再reverse回去即可得到(Q(x))

(R(x)=f(x)-g(x)Q(x))求得(R(x))

注意式子最后一步是在(mod {x^{n-m+1}})意义下的，那么(f,g)中次数高于(n-m)的部分不需要，这样可以减小一点常数吧

poly div(poly f,poly g,int n,int m){//被除数 除数 求商 
	rev(f,n);rev(g,m);g.clear(n-m+1,m);f.clear(n-m+1,n);g=Get_inv(g,n-m+1);
	poly ret=Mul(f,g,n-m+1,n-m+1);ret.clear(n-m+1,2*(n-m+1));
	rev(ret,n-m+1);return ret;
}
poly Get_mod(poly f,poly g,poly h,int n,int m){//被除数 除数 商 求余数 
	g=Mul(g,h,m,n-m+1);
	for(int i=0;i<m-1;++i)f[i]=dec(f[i],g[i]);
	return f;
}

多项式开根

前置芝士：

二次剩余（Cipolla算法）

若存在(x)使得(x^2equiv npmod p)，则称(n)为(mod p) 的二次剩余

勒让德符号

[left(dfrac{n}{p} ight)=egin{cases}1 p mid n ext{且$n$是$p$的二次剩余}\-1 p mid n ext{且$n$不是$p$的二次剩余}\0 pmid nend{cases} ]

欧拉判别准则

[left(dfrac{n}{p} ight)equiv n^{frac{p-1}{2}}pmod p ]

有(dfrac{p-1}{2})个数是(mod p) 意义下的二次非剩余

那么随机一个(ain[0,p))，令(omega^2equiv a^2-npmod p)。根据欧拉判别准则判断一下(omega)是不是(p)的二次非剩余，找到一个(p)的二次非剩余(omega)

找到这个(a)的期望次数是(2)

有结论：

[xequiv (a+omega)^{frac{p+1}2}pmod p ]

证明

两边平方：

[x^2equiv (a+omega)^{p+1} pmod p ]

[ecause (a+b)^pequiv a^p+b^ppmod p ]

[ herefore x^2equiv(a+omega)^p(a+omega)equiv(a^p+omega^p)(a+omega)pmod p ]

根据费马小定理(a^pequiv a^{p-1}cdot aequiv apmod p)

(omega^pequivomega(omega^2)^{frac{p-1}{2}}equiv omega(a^2-n)^{frac{p-1}{2}}equiv -omegapmod p)

带回去得

[(a-omega)(a+omega)equiv a^2-omega^2equiv npmod p ]

得证

那代码该怎么写？

类似虚数的东西，已知(omega^2)，求((a+omega)^{frac{p+1}2})

设(x=a+bomega)，则(x_1x_2=(a_1+b_1omega)(a_2+b_2omega)=(a_1a_2+b_1b_2omega^2)+(a_1b_2+a_2b_1)omega)

重载一下运算符即可

最后(x)取实部(a)就好了

两个解之和一定是(p)，那么如果求出来的(x>dfrac p2)，那么减回去就好了

这个是这道模板题的代码

struct Complex{int x,y;Complex(int xx,int yy){x=xx,y=yy;}};
inline Complex operator + (Complex a,Complex b){a.x=add(a.x,b.x),a.y=add(a.y,b.y);return a;}
inline Complex operator * (Complex a,Complex b){
	return Complex(add(mul(a.x,b.x),mul(a.y,1ll*b.y*w%mod)),add(mul(a.x,b.y),mul(a.y,b.x)));
}
inline Complex quick_pow(Complex a,int b){Complex ret(1,0);for(;b;b>>=1,a=a*a)if(b&1)ret=ret*a;return ret;}
inline int quick_pow(int a,int b){int ret=1;for(;b;b>>=1,a=mul(a,a))if(b&1)ret=mul(ret,a);return ret;}
inline int Euler(int a){return quick_pow(a,(mod-1)>>1);}
inline int Cipolla(int n){
	n%=mod;
	if(Euler(n)==mod-1)	return -1;
	int a;
	while(1){
		a=rand()%mod;w=dec(mul(a,a),n);
		if(Euler(w)==mod-1)break;
	}
	return quick_pow(Complex(a,1),(mod+1)>>1).x;
}
int T,n;
int main(){
	T=read();
	while(T--){
		n=read();mod=read();
		if(n==0){puts("0");continue;}
		int ans=Cipolla(n);
		if(ans==-1){puts("Hola!");continue;}
		if(ans>(mod>>1))ans=mod-ans;
		printf("%d %d
",ans,mod-ans);
	}
	return 0;
}

封装一下方便多项式用

namespace Cipolla{
	struct Complex{int x,y;Complex(int xx,int yy){x=xx,y=yy;}};int w;
	inline Complex operator + (Complex a,Complex b){a.x=add(a.x,b.x),a.y=add(a.y,b.y);return a;}
	inline Complex operator * (Complex a,Complex b){return Complex(add(mul(a.x,b.x),mul(a.y,1ll*b.y*w%mod)),add(mul(a.x,b.y),mul(a.y,b.x)));}
	inline Complex comp_quick_pow(Complex a,int b){Complex ret(1,0);for(;b;b>>=1,a=a*a)if(b&1)ret=ret*a;return ret;}
	inline int Euler(int a){return quick_pow(a,(mod-1)>>1);}
	inline int cipolla(int n){
		n%=mod;int a;
		while(1){
			a=rand()%mod;w=dec(mul(a,a),n);
			if(Euler(w)==mod-1)break;
		}
		int ret=comp_quick_pow(Complex(a,1),(mod+1)>>1).x;
		return (ret>(mod>>1))?mod-ret:ret;
	}
}

回到正题

假设已知(h(x)^2equiv f(x)pmod {x^{leftlceilfrac{n}{2} ight ceil}})，求(g(x)^2equiv f(x)pmod {x^n})

[g(x)-h(x)equiv 0pmod {x^{leftlceilfrac{n}{2} ight ceil}} ]

平方得

[g(x)^2-2h(x)g(x)+h(x)^2equiv 0 pmod {x^n} ]

(f(x)equiv g(x)^2pmod {x^n})代入得

[f(x)-2h(x)g(x)+h(x)^2equiv 0 pmod {x^n} ]

移项

[g(x)equivdfrac{f(x)+h(x)^2}{2h(x)}pmod {x^n} ]

边界条件：(g_0^2equiv f_0 pmod x)，用上述Cipolla算法求出二次剩余即可

poly Get_sqrt(poly f,int n){
	poly g;
	if(n==1){g[0]=cipolla(f[0]);return g;}
	g=Get_sqrt(f,(n+1)>>1);
	int len=init_pos(n<<1);
	poly a=Get_inv(g,n),b;cpy(n,b,f);
	NTT(b,len,1);NTT(a,len,1);NTT(g,len,1);
	for(int i=0;i<len;++i)	g[i]=mul(mul(add(b[i],mul(g[i],g[i])),a[i]),Inv(2));
	NTT(g,len,-1);int invn=Inv(len);
	for(int i=0;i<len;++i)	g[i]=(i<n)?mul(g[i],invn):0;
	return g;
}

多项式快速幂

已知(f(x))，求(g(x))，使得(g(x)equiv f^k(x)pmod {x^n})

数据范围：(nle 10^5,1le kle 10^{10^5})

推式子

两边取对数

[ln g(x)equiv kcdot ln f(x)pmod{x^n} ]

再取指数

[e^{ln g(x)}equiv e^{kcdot ln f(x)}pmod{x^n} ]

[g(x)equiv e^{kcdot ln f(x)}pmod{x^n} ]

但是(f_0)不一定等于(1)，那么(ln f(x))就没法用

设 (kmod (mod-1)=k_2)（费马小定理(a^pequiv apmod {p})）

那么我们就强制把(f_0)转成(1)

可以把每一位都除以(f_0)，最后把系数都乘上(f_0^k)，但是可能有(f_0)等于(0)的情况，这时候没法除

那么我们就找到最后一位不为(0)的位，设这是第(c+1)位（即(x^c)位）

那么只有(x^{k_2cdot c})位才有系数，后面的系数为(0)的个数为(k_2c)位

那么就相当于把后面的(c)位移回去，再把剩下的系数除以现在的最后一位，这样把最后一位变成了(1)

然后再按照(g(x)equiv e^{kcdot ln f(x)}pmod{x^n})做即可

最后把后面的(k_2c)位赋为(0)，把剩下的对应移回去即可

注意下面的细节：

要先判断(0)的位数会不会大于(n)，而且不能只判断取模以后的(k_2)，而是应该判断取模之前的(k)，如果全是(0)，那么直接输出
(k_2)的模数必须是(mod-1)

poly qpow(poly f,int n,int k1,int k2,int c){
	poly ans;if(1ll*c*k2>=n||c>=n)return ans;
	int v=Inv(f[c]),b=quick_pow(f[c],k2);for(int i=c;i<n;++i)f[i]=mul(f[i],v);
	for(int i=0,j=c;j<n;++i,++j)ans[i]=f[j];
	ans=Get_ln(ans,n);
	for(int i=0;i<n;++i)ans[i]=mul(ans[i],k1);
	ans=Get_exp(ans,n);
	for(int i=0;i<c*k2;++i)f[i]=0;
	for(int i=c*k2,j=0;i<n;++i,++j)f[i]=mul(ans[j],b);//注意要乘回去
	return f;
}
//主函数中
n=read();scanf("%s",s+1);int len=strlen(s+1);Read(n,f);
int c=0;while(f[c]==0&&c<n)++c;
for(int i=1;i<=len;++i){
	k1=add(mul(10,k1),s[i]-'0'),k2=10ll*k2%(mod-1)+s[i]-'0',k2=(k2>=mod-1)?k2-mod+1:k2;
	if(1ll*k1*c>n&&!f[0]){for(int i=0;i<n;++i)printf("0 ");return 0;}//特判0的个数大于n
}
Print(n,qpow(f,n,k1,k2,c));

优质板子

以下代码经过大力卡常，不建议在考场上使用，平时抄板用一用就好了

const int mod=998244353,G=3,N=(1<<20)+10;
namespace Math{
	int inv[N]={1,1},pos[N],mx;
	inline int add(int a,int b){return (a+b>=mod)?a+b-mod:a+b;}
	inline int dec(int a,int b){return (a-b<0)?a-b+mod:a-b;}
	inline void Add(int &a,int b){a+=(a+b>=mod)?b-mod:b;}
	inline void Dec(int &a,int b){a-=(a<b)?b-mod:b;}
	inline int mul(int a,int b){return 1ll*a*b%mod;}
	inline int quick_pow(int a,int b){int ret=1;for(;b;b>>=1,a=mul(a,a))if(b&1)ret=mul(a,ret);return ret;}
	inline void init_inv(int n){
		mx=n;
		for(int i=2;i<=n;++i)inv[i]=dec(mod,mul(mod/i,inv[mod%i]));
	}
	inline int Inv(int a){if(a<=mx)return inv[a];else return quick_pow(a,mod-2);}
	inline void init_pos(int cnt,int len){
		for(int i=0;i<len;++i)pos[i]=(pos[i>>1]>>1)|((i&1)<<cnt);
	}
}
using namespace Math;
namespace Cipolla{
    struct Complex{int x,y;Complex(int xx,int yy){x=xx,y=yy;}};int w;
    inline Complex operator + (Complex a,Complex b){a.x=add(a.x,b.x),a.y=add(a.y,b.y);return a;}
    inline Complex operator * (Complex a,Complex b){return Complex(add(mul(a.x,b.x),mul(a.y,1ll*b.y*w%mod)),add(mul(a.x,b.y),mul(a.y,b.x)));}
    inline Complex comp_quick_pow(Complex a,int b){Complex ret(1,0);for(;b;b>>=1,a=a*a)if(b&1)ret=ret*a;return ret;}
    inline int Euler(int a){return quick_pow(a,(mod-1)>>1);}
    inline int cipolla(int n){
        int a;
        while(1){
            a=rand();w=dec(mul(a,a),n);
            if(Euler(w)==mod-1)break;
        }
        int ret=comp_quick_pow(Complex(a,1),(mod+1)>>1).x;
        return (ret>(mod>>1))?mod-ret:ret;
    }
}
#define vec vector<int> 
struct poly{
	vec v;
	inline poly(int w=0):v(1){v[0]=w;}
	inline poly(const vec&_f):v(_f){}
	inline int& operator[](int x){if(v.size()<=x)v.resize(x+1);return v[x];}
	inline void resize(int r){v.resize(r);}
	inline int size(){return v.size();}
	inline void rev(){reverse(v.begin(),v.end());}
	inline void Read(int n){v.resize(n);for(int i=0;i<n;++i)scan(v[i]);}
	inline void Print(int n){if(v.size()<n)v.resize(n);for(int i=0;i<n;++i)putint(v[i],' ');pc('
');}
	inline poly slice(int x){
		if(x<v.size())return vec(v.begin(),v.begin()+x);
		poly res(v);res.resize(x);
		return res;
	}
};
#define ull unsigned long long
const ull Mod=998244353; 
namespace Basic{
	inline void cpy(int n,poly &f,poly f1){for(int i=0;i<n;++i)f[i]=f1[i];}
	ull f1[N];
	int Wn[N],Log2[N];
	inline void init_poly(int n){
		int cnt1=0;while(n)n>>=1,++cnt1;
		cnt1=(1<<cnt1+1);
		init_inv(cnt1);
		Log2[1]=0;
		for(int i=2;i<=cnt1;++i)Log2[i]=Log2[i>>1]+1;
		int tot=0;
		for(int i=1,base;i<=cnt1;i<<=1){
			base=quick_pow(G,(mod-1)/(i<<1));
			Wn[++tot]=1;for(int j=1;j<i;++j)++tot,Wn[tot]=1ll*Wn[tot-1]*base%mod;
		}
	}
	inline void NTT(poly &f,int len,bool flag){ 
		for(int i=0;i<len;++i)f1[pos[i]]=f[i];
		for(int mid=1,k=2;mid<len;mid<<=1,k<<=1)
			for(int i=0;i<len;i+=k)
				for(int j=0;j<mid;++j){
					ull x=f1[j+i],y=Wn[mid+j]*f1[j+mid+i]%Mod;
					f1[i+j]=x+y,f1[i+j+mid]=Mod+x-y;
				}
		for(int i=0;i<len;++i)f1[i]%=Mod;
		if(!flag){
			reverse(f1+1,f1+len);
			int invn=Inv(len);
			for(int i=0;i<len;++i)f1[i]=1ll*f1[i]*invn%mod;
		}
		for(int i=0;i<len;++i)f[i]=f1[i];
	}
	inline poly Mul(poly a,poly b,int n,int m){
		a.resize(n);b.resize(m);
		int cnt=Log2[n+m-1],len=1<<(cnt+1);
		init_pos(cnt,len);
		NTT(a,len,1);NTT(b,len,1);
		for(int i=0;i<len;++i)a[i]=mul(a[i],b[i]);
		NTT(a,len,0);
		return a.slice(m+n-1);
	}
	inline poly der(poly f,int n){poly ret;ret.resize(n);for(int i=1;i<n;++i)ret[i-1]=mul(f[i],i);return ret;}
	inline poly inter(poly f,int n){poly ret;ret.resize(n);for(int i=1;i<n;++i)ret[i]=mul(f[i-1],Inv(i));return ret;}
	inline poly poly_inv(poly f,int n){
		poly g;g[0]=Inv(f[0]);poly g0,d;
		for(int len=2,cnt=0;(len>>1)<n;len<<=1,++cnt){
			g0=g;init_pos(cnt,len);d=f.slice(len);
			NTT(g0,len,1);NTT(d,len,1);
			for(int i=0;i<len;++i)d[i]=1ll*d[i]*g0[i]%mod;
			NTT(d,len,0);
			fill(d.v.begin(),d.v.begin()+(len>>1),0);
			NTT(d,len,1);
			for(int i=0;i<len;++i)d[i]=1ll*d[i]*g0[i]%mod;
			NTT(d,len,0);
			fill(d.v.begin(),d.v.begin()+(len>>1),0);
			for(int i=0;i<len;++i)g[i]=dec(g[i],d[i]);
		}
		return g.slice(n);
	}
	inline poly div(poly f,poly g,int n,int m){
		poly ret;
		if(n==1){ret[0]=1ll*f[0]*Inv(g[0])%mod;return ret;}
		int cnt=Log2[n],len=1<<(cnt+1),len1=len>>1;
		poly g0=g.slice(len1),q0,f0=f.slice(len1);
		g0=poly_inv(g0,len1);
		init_pos(cnt,len);
		NTT(g0,len,1);NTT(f0,len,1);
		for(int i=0;i<len;++i)q0[i]=1ll*g0[i]*f0[i]%mod;
		NTT(q0,len,0);q0.resize(len1);
		ret=q0;
		NTT(g,len,1);NTT(q0,len,1);
		for(int i=0;i<len;++i)q0[i]=1ll*q0[i]*g[i]%mod;
		NTT(q0,len,0);
		fill(q0.v.begin(),q0.v.begin()+len1,0);
		for(int i=len1;i<len;++i)q0[i]=dec(q0[i],f[i]);
		NTT(q0,len,1);
		for(int i=0;i<len;++i)q0[i]=1ll*q0[i]*g0[i]%mod;
		NTT(q0,len,0);
		for(int i=len1;i<len;++i)ret[i]=dec(ret[i],q0[i]);
		return ret.slice(n);
	}
	inline poly poly_ln(poly f,int n){
		return inter(div(der(f,n),f,n,n),n);
	}
	namespace EXP{
		const int logB=4;
		const int B=16;
		poly f,ret,g[30][B];
		inline void exp(int lim,int l,int r){
			if(r-l<=64){
				for(int i=l;i<r;++i){
					ret[i]=(!i)?1:1ll*ret[i]*inv[i]%mod;
					for(int j=i+1;j<r;++j) Add(ret[j],1ll*ret[i]*f[j-i]%mod);
				}
				return ;
			}
			int k=(r-l)/B;
			poly bl[B];
			for(int i=0;i<B;++i) bl[i].resize(k<<1);
			int len=1<<lim-logB+1;
			for(int i=0;i<B;++i){
				if(i>0){
					init_pos(Log2[len]-1,len);NTT(bl[i],len,0);
					for(int j=0;j<k;++j)
						Add(ret[l+i*k+j],bl[i][j+k]);
				}
				exp(lim-logB,l+i*k,l+(i+1)*k);
				if(i<B-1){
					poly H;H.resize(k<<1);
					for(int j=0;j<k;++j) H[j]=ret[j+l+i*k];
					init_pos(Log2[len]-1,len);;NTT(H,len,1);
					for(int j=i+1;j<B;++j)
						for(int t=0;t<(k<<1);++t) Add(bl[j][t],1ll*H[t]*g[lim][j-i-1][t]%mod); 
				}
			}
		}
		inline void init_exp(){
			for(int i=0;i<f.v.size();++i) f[i]=1ll*f[i]*i%mod;
			int mx=Log2[f.v.size()]+1;
			for(int lim=mx;lim>=logB;lim-=logB){
				int bl=1<<(lim-logB),tot=0,ll=1<<(lim-logB+1);
				init_pos(Log2[ll]-1,ll);
				for(int i=0;i<B-1;++i){
					g[lim][i].resize(bl<<1);
					for(int j=0;j<(bl<<1);++j) g[lim][i][j]=f[j+bl*i];
					NTT(g[lim][i],ll,1);
				}
			}
		}
		//非递归版 
		/*inline poly poly_exp(poly f,int n){
			poly g;g[0]=1;poly g0,h0,dg0,df0,df,g1;
			for(int len=2,len1,cnt=0;(len>>1)<n;len<<=1,++cnt){
				len1=len>>1;
				g0=g;g1=g;dg0=der(g0,len1);df0=der(f.slice(len1),len1);
				df=der(f.slice(len),len);h0=poly_inv(g0,len1);
				init_pos(cnt-1,len1);
				NTT(dg0,len1,1);NTT(h0,len1,1);
				for(int i=0;i<len1;++i)dg0[i]=1ll*dg0[i]*h0[i]%mod;
				NTT(dg0,len1,0);
				for(int i=0;i<len;++i)dg0[i]=dec(dg0[i],df[i]);
				for(int i=0;i<len1-1;++i)dg0[i+len1]=add(dg0[i+len1],dg0[i]),dg0[i]=0;
				NTT(g0,len1,1);
				for(int i=0;i<len1;++i)h0[i]=1ll*g0[i]*h0[i]%mod;
				NTT(h0,len1,0);h0[0]=dec(h0[0],1);
				for(int i=0;i<len1;++i)h0[i+len1]=add(h0[i+len1],h0[i]),h0[i]=0;
				init_pos(cnt,len);
				NTT(h0,len,1);NTT(df0,len,1);
				for(int i=0;i<len;++i)h0[i]=1ll*df0[i]*h0[i]%mod;
				NTT(h0,len,0);h0.resize(len);
				fill(h0.v.begin(),h0.v.begin()+len1,0);
				for(int i=0;i<len;++i)h0[i]=dec(dg0[i],h0[i]);
				h0=inter(h0,len);
				NTT(g1,len,1);NTT(h0,len,1);
				for(int i=0;i<len;++i)g1[i]=1ll*h0[i]*g1[i]%mod;
				NTT(g1,len,0);
				for(int i=len1;i<len;++i)g[i]=dec(g[i],g1[i]);
			}
			return g;
		}*/
	}
	inline poly poly_exp(poly f,int n){
		EXP::f=f;
		EXP::init_exp();
		EXP::exp(Log2[n]+1,0,1<<Log2[n]+1);
		return EXP::ret.slice(n);
	}
	inline poly poly_sqrt(poly f,int n){
		poly g,g0,h,b,a,c;g[0]=Cipolla::cipolla(f[0]);
		h[0]=Inv(g[0]);g0[0]=g[0];g0[1]=g[0];int iv2=Inv(2);
		init_pos(0,1);
		for(int len=2,len1,cnt=0;(len>>1)<n;len<<=1,++cnt){
			len1=len>>1;
			for(int i=0;i<len1;++i)b[i]=1ll*g0[i]*g0[i]%mod;
			NTT(b,len1,0);
			for(int i=0;i<len1;++i)b[i+len1]=dec(b[i],f[i]),b[i]=0;
			for(int i=len1;i<len;++i)b[i]=dec(b[i],f[i]);		
			a=h;a.resize(len1);
			init_pos(cnt,len);
			NTT(a,len,1);NTT(b,len,1);
			for(int i=0;i<len;++i)b[i]=1ll*a[i]*b[i]%mod;
			NTT(b,len,0);
			for(int i=len1;i<len;++i)g[i]=dec(0,1ll*b[i]*iv2%mod);
			if(len>=n)break;
			g0=g;NTT(g0,len,1);
			for(int i=0;i<len;++i)c[i]=1ll*a[i]*g0[i]%mod;
			NTT(c,len,0);
			fill(c.v.begin(),c.v.begin()+len1,0);
			NTT(c,len,1);
			for(int i=0;i<len;++i)c[i]=1ll*a[i]*c[i]%mod;
			NTT(c,len,0);
			for(int i=len1;i<len;++i)h[i]=dec(h[i],c[i]);
		}
		return g.slice(n);
	}
	inline poly poly_pow(poly f,int n,int k){
		int c=0;while(!f[c]&&1ll*c*k<n)++c;poly g;
		if(1ll*c*k>=n){g.resize(n);return g;}
		int iv=Inv(f[c]),b=quick_pow(f[c],k);
		for(int i=c;i<n;++i)f[i]=1ll*iv*f[i]%mod;
		for(int j=c;j<n;++j)g[j-c]=f[j];
		g=poly_ln(g,n);
		for(int i=0;i<n;++i)g[i]=1ll*g[i]*k%mod;
		g=poly_exp(g,n);
		for(int i=c*k,j=0;i<n;++i,++j)f[i]=1ll*g[j]*b%mod;
		fill(f.v.begin(),f.v.begin()+c*k,0);
		return f; 
	}
}
using namespace Basic;
namespace DIVISION{
	inline poly divide(poly F,poly G,int n,int m){
		if(F.v.size()<G.v.size()){G.resize(1);G[0]=0;return G;}
		F.rev();int p=n-m+1;poly INVG=G;INVG.rev();INVG=poly_inv(INVG,INVG.size());
		F=Basic::Mul(F,INVG,p,p).slice(p);
		F.rev();
		return F;
	}
	inline poly module(poly F,poly G,poly Q,int n,int m,int q){
		q=Q.v.size();
		G=Basic::Mul(G,Q,m,q);
		for(int i=0;i<m;++i)Dec(F[i],G[i]);
		return F.slice(m-1);
	}
}
inline poly operator -(poly F,poly G){for(int i=0;i<max(F.size(),G.size());++i)Dec(F[i],G[i]);return F;}
inline poly operator +(poly F,poly G){for(int i=0;i<max(F.size(),G.size());++i)Add(F[i],G[i]);return F;}
inline poly operator *(poly F,poly G){return Basic::Mul(F,G,F.v.size(),G.v.size());}
inline poly operator /(poly F,poly G){return DIVISION::divide(F,G,F.v.size(),G.v.size());}
inline poly operator %(poly F,poly G){
	int n=F.v.size(),m=G.v.size();
	return DIVISION::module(F,G,DIVISION::divide(F,G,n,m),n,m,n-m+1);
}

相关阅读:
RabbitMq 集群配置
 获取 input 单选框和多选框的值
 js 获取通过 ”？“ 或者 ”&“ url 传过来参数值
 Java 对文件的读取操作
 java 链接jdbc
了解EBP寄存器
 节后后遗症
 [转]web service实现原理与异步调用
 Javascript实现无刷新分页
 邮件发送
原文地址：https://www.cnblogs.com/harryzhr/p/14736755.html