虚树
干啥用的呢?看道例题
P2495 [SDOI2011]消耗战
简要题意
一棵(n)个节点的树,边有边权
(m)次询问,每次询问有(k)个关键点,要断掉一些边(花费为边权),使得(1)不能到达任何关键点且花费最小
(sum k le 5 imes 10^5)
先考虑一次询问的情况
树形DP
设(dp[u])表示(u)及其子树全都与(1)断开所需要的最小花费,设(mn[u])表示(u)到(1)的路径上的最小值
对于关键点:必须把自己到根的路径断开一条,即(dp[u]=mn[u])
对于其他点,有两种情况
- 自己到根节点的最小值
- 自己所有的有关键节点的儿子都断开
即(dp[u]=min(sumlimits_{vin to[u]}dp[v],mn[u]))
但是这样对于多次询问T的起飞
再考虑多次询问
很明显有贡献的点并不是那么多
那么就要把这些有贡献的点找出来重新建树,这样复杂度就是(sum k)
理性理解一下:有贡献的点只能是关键点和关键点两两的LCA
那么怎么去找这些LCA呢
首先我们维护一条最右链,用一个栈存储。这样的好处是:很多点的LCA是相同的,这样大大减少找到所有LCA所用时间
- 第一种情况:自己是链顶的儿子,直接插入栈顶即可

- 第二种情况:自己不是链顶的儿子
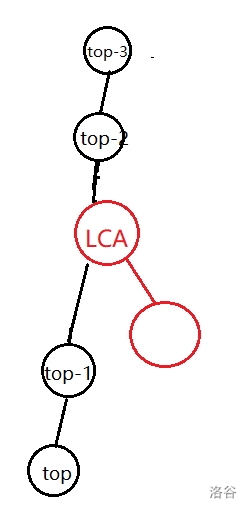
把所有深度大于LCA的点都弹出,然后把LCA和自己入栈。出栈的时候建边,注意,离LCA最近的那个点(图中的(stac[top-1])要与LCA连边,不然建出来的树就不满足父子关系了)
注意LCA若已经在链上就不要多次插入
最后把留在链中的点都弹出(边弹边建边)
还有一个细节:在栈底先插入一个(1),这样既保证(1)一直不会被弹出((dep[1])是最小的),这样循环不会有边界问题;同时也保证了(1)一定有连边
找LCA可以(O(log n)),当然(O(nlog n))预处理(O(1))查询更好
int stac[N],top;
inline void push(int val){stac[++top]=val;}
inline void pop(){
g2.adde(stac[top],stac[top-1],mn[stac[top]]);//边出栈边连边
--top;
}
inline bool cmp(int a,int b){return id[a]<id[b];}
void build(){
sort(node+1,node+1+k,cmp);//排序
top=0;push(1);
for(int i=1;i<=k;++i){
int lca=LCA(node[i],stac[top]);
if(lca==stac[top]){push(node[i]);continue;}//是栈顶的儿子,直接插入
while(dep[stac[top-1]]>dep[lca])pop();
g2.adde(stac[top],lca,mn[stac[top]]);--top;//连向LCA
if(lca!=stac[top])push(lca);
push(node[i]);
}
while(top>1)pop();
}
这里排序是按(dfs)序排序,这样保证了最右链
剩下的就是简单的树形DP了
直接上代码
long long dp[N];
bool is_node[N];//是否是关键节点
void dfs2(int u,int fat,long long pre){
long long sum=0;dp[u]=0;
for(int i=g2.head[u],v;i;i=g2.e[i].next){
v=g2.e[i].to;if(v==fat)continue;
dfs2(v,u,g2.e[i].len);sum+=dp[v];
}
g2.head[u]=0;
if(u==1)dp[u]=sum;
else if(is_node[u])dp[u]=pre;
else dp[u]=min(sum,pre);
}
还要注意建边之后清空必须一个一个清,不然退化成(O(n))
这道题的完整代码
const int N=3e5+5,LOG2=21;
struct G{
struct Edge{int to,next,len;}e[N<<1];
int head[N],cnt;
inline void add(int u,int v,int w){e[++cnt].next=head[u];head[u]=cnt;e[cnt].len=w;e[cnt].to=v;}
inline void adde(int u,int v,int w){add(u,v,w);add(v,u,w);}
}g1,g2;
int Log2[N<<1],n;
int mn[N]/*根到u的最小值*/,dep[N],st[N<<1][LOG2],id[N],tot;
int m,node[N],k;
inline int minn(int a,int b){return (dep[a]<dep[b])?a:b;}
void dfs1(int u,int fat){
st[++tot][0]=u;id[u]=tot;dep[u]=dep[fat]+1;
for(int i=g1.head[u],v;i;i=g1.e[i].next){
v=g1.e[i].to;if(v==fat)continue;
mn[v]=min(mn[u],g1.e[i].len);
dfs1(v,u);st[++tot][0]=u;
}
}
inline void pre_work(){
dfs1(1,0);
for(int i=1;i<=tot;++i)Log2[i]=Log2[i-1]+(1<<Log2[i-1]==i);
for(int i=1;i<Log2[tot];++i)//ST表O(1)求LCA
for(int j=1;j+(1<<i)<=tot;++j)
st[j][i]=minn(st[j][i-1],st[j+(1<<(i-1))][i-1]);
}
inline int LCA(int x,int y){
if(x==y)return x;
if(id[x]>id[y])swap(x,y);
x=id[x],y=id[y];int len=Log2[y-x+1]-1;
return minn(st[x][len],st[y-(1<<len)+1][len]);
}
int stac[N],top;
inline void push(int val){stac[++top]=val;}
inline void pop(){
g2.adde(stac[top],stac[top-1],mn[stac[top]]);//边出栈边连边
--top;
}
inline bool cmp(int a,int b){return id[a]<id[b];}
void build(){
sort(node+1,node+1+k,cmp);//排序
top=0;push(1);
for(int i=1;i<=k;++i){
int lca=LCA(node[i],stac[top]);
if(lca==stac[top]){push(node[i]);continue;}//是栈顶的儿子,直接插入
while(dep[stac[top-1]]>dep[lca])pop();
g2.adde(stac[top],lca,mn[stac[top]]);--top;//连向LCA
if(lca!=stac[top])push(lca);
push(node[i]);
}
while(top>1)pop();
}
long long dp[N];
bool is_node[N];
void dfs2(int u,int fat,long long pre){
long long sum=0;dp[u]=0;
for(int i=g2.head[u],v;i;i=g2.e[i].next){
v=g2.e[i].to;if(v==fat)continue;
dfs2(v,u,g2.e[i].len);sum+=dp[v];
}
g2.head[u]=0;
if(u==1)dp[u]=sum;
else if(is_node[u])dp[u]=pre;
else dp[u]=min(sum,pre);
}
int main(){
n=read();
memset(mn,0x3f,sizeof(mn));
for(int i=1,u,v,w;i<n;++i){u=read();v=read();w=read();g1.adde(u,v,w);}
pre_work();m=read();
while(m--){
k=read();for(int i=1;i<=k;++i)node[i]=read(),is_node[node[i]]=1;
build(); dfs2(1,0,0);
for(int i=1;i<=k;++i)is_node[node[i]]=0;g2.cnt=0;
printf("%lld
",dp[1]);
}
return 0;
}