动态规划算法

一 从斐波那契数列看动态规划

斐波那契数列：
　　Fn= Fn−1 + Fn−2
使⽤递归和⾮递归的⽅法来求解斐波那契数列的第n项

1 递归实现

# 子问题的重复计算
def fibnacci(n):
    if n == 1 or n == 2:
        return 1
    else:
        return fibnacci(n - 1) + fibnacci(n - 2)

2 非递归实现

# 动态规划（DP）的思想 = 递推式
def fibnacci_no_recurision(n):
    f = [0, 1, 1]
    if n > 2:
        for i in range(n - 2):
            num = f[-1] + f[-2]
            f.append(num)
    return f[-1]

print(fibnacci_no_recurision(100))

二  钢条切割问题

某公司出售钢条，出售价格与钢条⻓度之间的关系如下表：

问题：现有⼀段⻓度为n的钢条和上⾯的价格表，求切割钢条⽅案，使得总收益最⼤

⻓度为4的钢条的所有切割⽅案如下：（c⽅案最优）

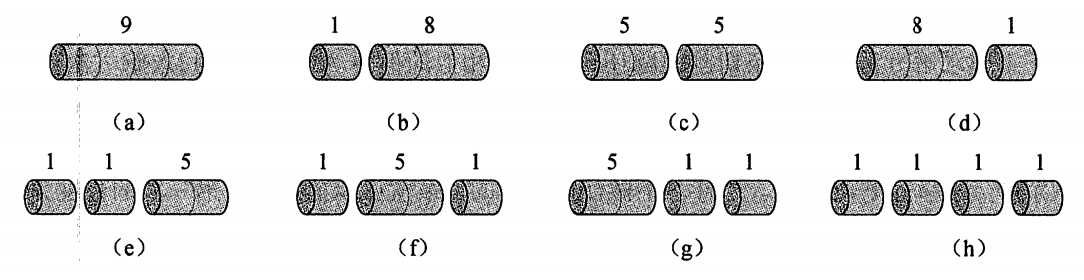
⻓度为n的钢条的不同切割⽅案有⼏种？

 

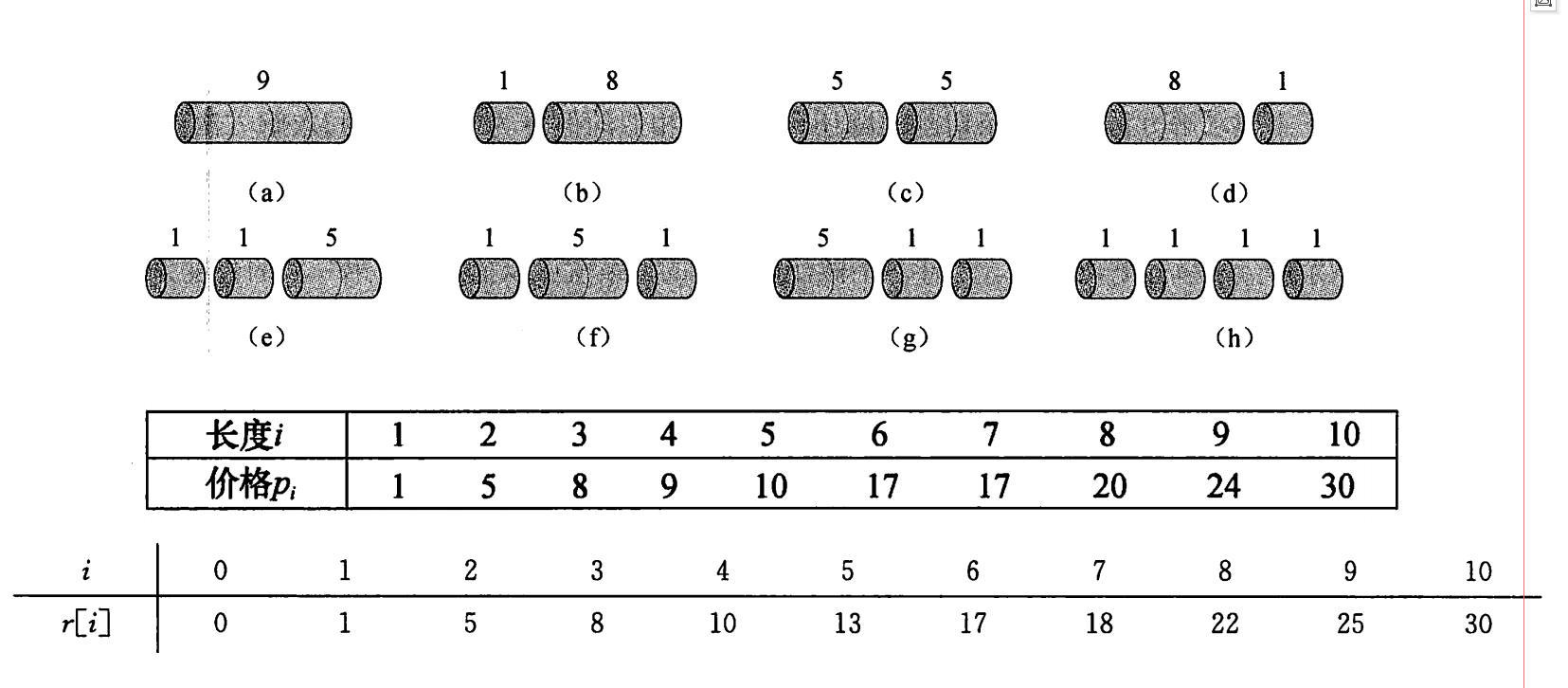
设⻓度为n的钢条切割后最优收益值为r可以得出递推式：

• rn = max(pn, r1 + rn!1, r2 + rn!2,··· , rn!1 + r1)

第⼀个参数pn表示不切割

其他n-1个参数分别表示另外n-1种不同切割⽅案，对⽅案i=1,2,...,n-1

• 将钢条切割为⻓度为i和n-i两段
• ⽅案i的收益为切割两段的最优收益之和

考察所有的i选择其中收益最⼤的⽅案

三 钢条切割问题之最优子结构

可以将求解规模为n的原问题，划分为规模更⼩的⼦问题：完成⼀次切割后，可以将产⽣的两段钢条看成两个独⽴的钢条切个问题。 
组合两个⼦问题的最优解，并在所有可能的两段切割⽅案中选取组合收益最⼤的，构成原问题的最优解。 
钢条切割满⾜最优⼦结构：问题的最优解由相关⼦问题的最优解组合⽽成，这些⼦问题可以独⽴求解

钢条切割问题还存在更简单的递归求解⽅法

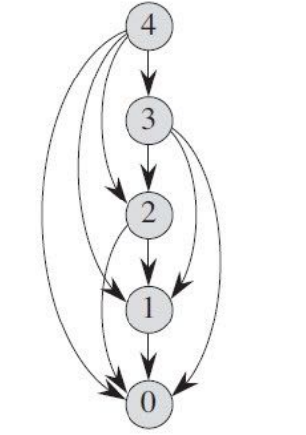
从钢条的左边切割下⻓度为i的⼀段，只对右边剩下的⼀段继续进⾏切割，左边的不再切割

递推式简化为 ：

　　

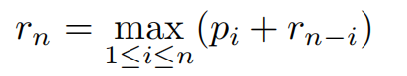
不做切割的⽅案就可以描述为：左边⼀段⻓度为n，收益为pn，剩余⼀段⻓度为0，收益为r0=0。

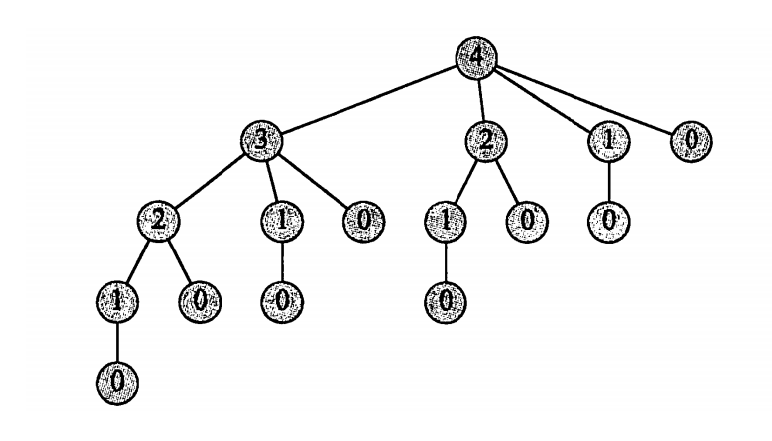
(1) 自顶向下递归实现

时间复杂度 O(2n)实现效果差

递归算法由于重复求解相同⼦问题，效率极低

动态规划的思想：

• 每个⼦问题只求解⼀次，保存求解结果
• 之后需要此问题时，只需查找保存的结果

p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]

def cut_rod_recurision(p, n):
    if n == 0:
        return 0
    else:
        res = p[n]
        for i in range(1, n):
            res = max(res, cut_rod_recurision(p, i) + cut_rod_recurision(p, n - i))
    return res


print(cut_rod_recurision(p, 20))


def cut_rod_recurision(p, n):
    if n == 0:
        return 0
    else:
        res = 0
        for i in range(1, n + 1):
            res = max(res, p[i] + cut_rod_recurision(p, n - i))
        return res


print(cut_rod_recurision(p, 20))

 (2) 自底向上递归实现

时间复杂度：O(n2 )

p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]

def cut_rop_dp(p, n):
    r = [0]
    for i in range(1, n + 1):
        res = 0
        for j in range(1, i + 1):
            res = max(res, p[j] + r[i - j])
        r.append(res)
    return r[n]


print(cut_rop_dp(p, 20))

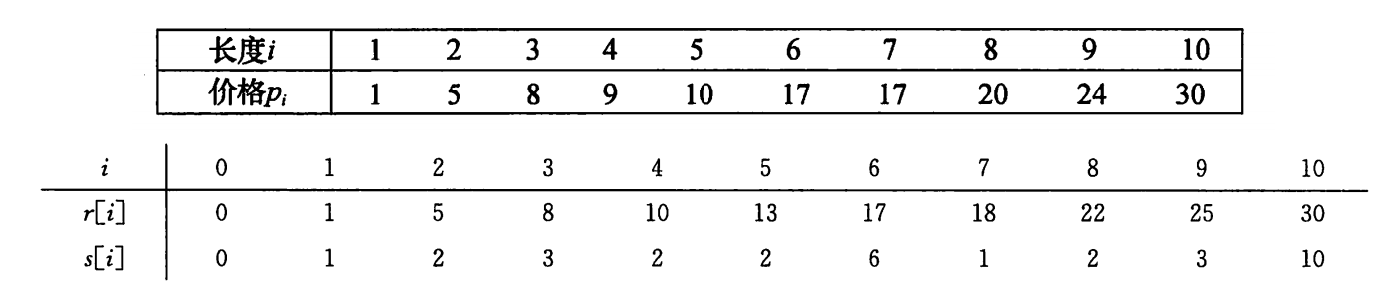
(3) 钢条切割重构解

如何修改动态规划算法，使其不仅输出最优解，还输出最优切割⽅案？
对每个⼦问题，保存切割⼀次时左边切下的⻓度

四 最⻓公共子序列

个序列的⼦序列是在该序列中删去若⼲元素后得 到的序列。
例：“ABCD”和“BDF”都是“ABCDEFG”的⼦序列

最⻓公共⼦序列（LCS）问题：给定两个序列X和Y，求X和Y⻓度最⼤的公共⼦序列。
例：X="ABBCBDE" Y="DBBCDB" LCS(X,Y)="BBCD"

应⽤场景：字符串相似度⽐对

 最优解的递推式：

c[i,j]表示Xi和Yj的LCS⻓度

　　

 例如：要求a="ABCBDAB"与b="BDCABA"的LCS：

由于最后⼀位"B"≠"A"：因此LCS(a,b)应该来源于LCS(a[:-1],b)与LCS(a,b[:-1])中更⼤的那⼀个

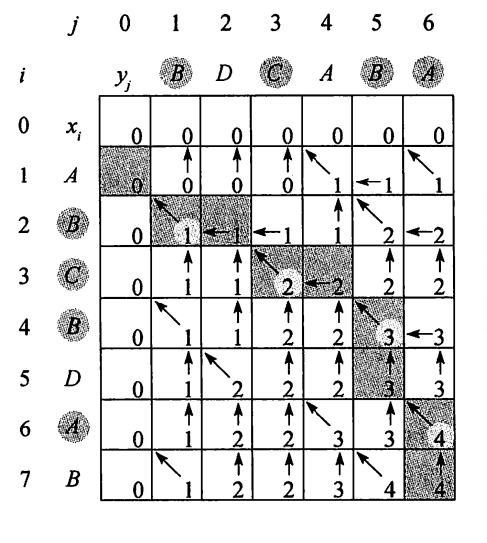
计算公共最长子序列长度实现代码：

def lcs_length(x, y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if x[i - 1] == y[j - 1]:  # i j位置上的字符匹配的时候， 来自于左上方+1
                c[i][j] = c[i - 1][j - 1] + 1
            else:
                c[i][j] = max(c[i - 1][j], c[i][j - 1])
    return c[m][n]

print(lcs_length("ABCDBAB", "BDCABA"))

实现输出最⻓公共⼦序列的值

def lcs(x, y):
    '''
    记录最长公共子序列路径
    :param x:
    :param y:
    :return:
    '''
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    b = [[0 for _ in range(n + 1)] for _ in range(m + 1)]  # 1 左上方 2 上方 3 左方
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if x[i - 1] == y[j - 1]:  # i j位置上的字符匹配的时候， 来自于左上方+1
                c[i][j] = c[i - 1][j - 1] + 1
                b[i][j] = 1
            elif c[i - 1][j] > c[i][j - 1]:  # 来自于上方
                c[i][j] = c[i - 1][j]
                b[i][j] = 2
            else:
                c[i][j] = c[i][j - 1]
                b[i][j] = 3
    return c[m][n], b


def lcs_traceback(x, y):
    c, b = lcs(x, y)
    i = len(x)
    j = len(y)
    res = []

    while i > 0 and j > 0:
        if b[i][j] == 1:  # 来自左上方=>匹配
            res.append(x[i - 1])
            i -= 1
            j -= 1
        elif b[i][j] == 2:  # 来自上方=>不匹配
            i -= 1
        else:  # == 来自左方=>不匹配
            j -= 1
    return "".join(reversed(res))


# 输出公共最长子序列
print(lcs_traceback("ABCBDAB", "BDCABA"))

五 动态规划

什么问题可以使⽤动态规划⽅法？

最优⼦结构

• 原问题的最优解中涉及多少个⼦问题
• 在确定最优解使⽤哪些⼦问题时，需要考虑多少种选择

重叠⼦问题