选择排序

一.简单选择排序（不稳定）

1.基本思想：通过n-i次关键字间的比较，从n-i+1个记录中选出关键字最小的记录，并和第i个记录交换。

template <typename Comparable>
void selectSort (vector<Comparable>&a)
{//找出按从小到大排序应排在第i个位置的记录并和第i个元素交换
　　for ( int i = 0; i < a.size()-1; ++i)
　　{
　　　　Comparable temp = a[i];
　　　　int index = i;
　　　　for ( int j = i + 1; j < a.size(); ++j )
　　　　{
　　　　　　if ( a[j] < temp )
　　　　　　{
　　　　　　　　temp = a[j];
　　　　　　　　index = j;
　　　　　　}
　　　　}
       if (index!=i)
       {
　　　　    temp = a[i];
　　　　    a[i] = a[index];
　　　　    a[index] = temp;
       }
　　}
}    

 eg: 5',4,5,2,9 经过排序后 2,4,5,5',9，两个5的位置调换了，所以不稳定

python版本

def selectSort(data):
    """选择排序"""
    n = len(data)

    for i in range(0, n-1):
        index = i
        for j in range(i+1, n):
            if data[j] < data[index]:
                index = j

        if index != i:
            data[i], data[index] = data[index], data[i]

    return data

 二.堆排序（不稳定）

堆的性质：即任何一非叶节点的关键字不大于或者不小于其左右孩子节点的关键字。

主要步骤：构建初始堆和调堆

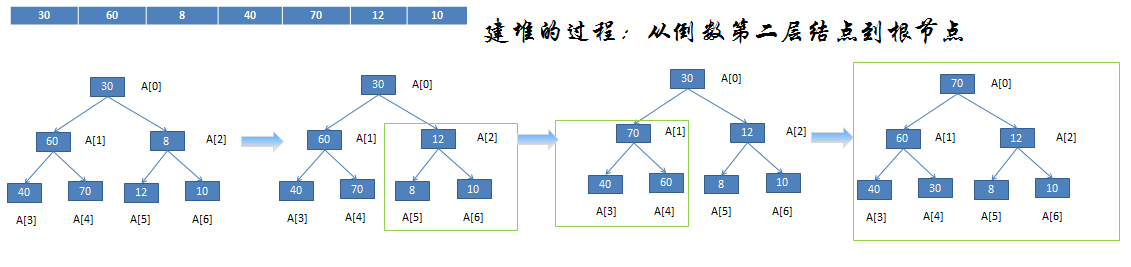
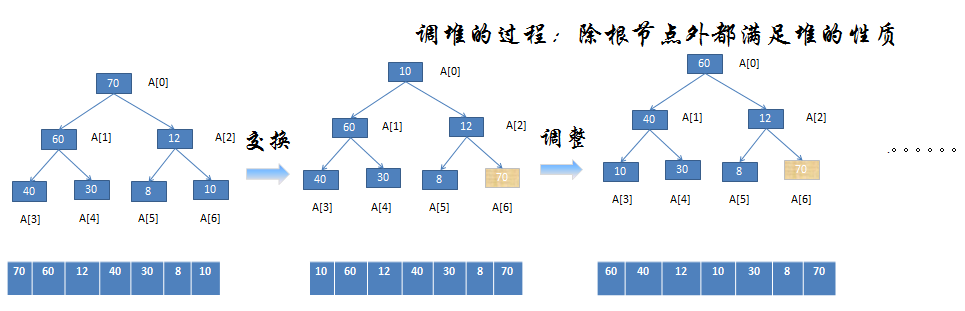
int leftChild ( int i )
{
    return 2 * i + 1;
}

template < typename Comparable >
void adjust ( vector<Comparable> & a, int i, int n )
{//调整由元素i到n构成的堆
    int child;
    Comparable temp = a[i];
    
    while ( leftChild(i) <= n ) 
    { 
        //如果有右孩子，则取两个孩子中的最大值
        child = leftChild ( i );
        if( child < n  && a[ child ] < a[ child + 1] )
            child++;
        if( temp < a[ child ] )
        {//往下移
            a[ i ] = a[ child ];
　　　　　　　　i = child;
        }
        else
            break;
　　　　
    }
    //找到插入位置，进行插入
    a[ i ] = temp;
}
template < typename Comparable >
void heapSort ( vector<Comparable> & a)
{//对下标为0到a.size()-1的元素按从大到小顺序进行排序
    for ( int i = a.size() / 2 ; i >= 0; i-- )
        adjust(a, i, a.size()-1);
    for ( int j = a.size() - 1; j > 0; j-- )
    {
        Comparable temp = a[j];//交换堆顶和最后一个元素
        a[j] = a[0];
        a[0] = temp;
        adjust(a,0,j-1);//重新调整堆，最后第j个元素用来存储堆顶，
                            //不用再考虑.
    }
}

 python版本

def leftChild(i):
    """计算指定节点的左孩子下标"""
    return 2 * i + 1

def adjust(data, i, n):
    """调整堆"""
    temp = data[i]

    while leftChild(i) <= n:
        child = leftChild(i)
        if child < n and data[child] < data[child + 1]:
            child += 1

        if temp < data[child]:
            data[i] = data[child]
            i = child
        else:
            break

    data[i] = temp


def heapSort(data):
    """堆排序"""
    n = len(data)

    for i in range(n//2,-1,-1):
        adjust(data, i, n-1)

    for j in range(n-1, 0, -1):
        data[0], data[j] = data[j], data[0]
        adjust(data, 0, j-1)

    return data

 PS：当0号元素为大顶堆堆顶时，第一轮交换就会被置于最后一位，所以，如果还有相同的数字，顺序一定会被打乱。