二进制:二进制数据是用0和1两个数码来表示的数。它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”。计算机中的二进制则是一个非常微小的开关,用“开”来表示1,“关”来表示0。
二进制的计算由计算机内的门电路进行,门电路可以有一个或多个输入端,但只有一个输出端。
原码(true form)是一种计算机中对数字的二进制定点表示方法。原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为0,负数该位为1(0有两种表示:+0和-0),其余位表示数值的大小。
简单直观;例如,我们用8位二进制表示一个数,+11的原码为00001011,-11的原码就是10001011
反码:规定 正数的反码与原码相同。负数:负数的反码,符号位为“1”,数值部分按位取反。
补码:规定 正数:正数的补码和原码相同。负数:负数的补码则是符号位为“1”。并且,这个“1”既是符号位,也是数值位。数值部分按位取反后再在末位(最低位)加1。也就是“反码+1”。
1、门电路
1.1、定义
门电路:“门”是这样的一种电路:它规定各个输入信号之间满足某种逻辑关系时,才有信号输出,通常有下列三种门电路:与门、或门、非门(反相器)。从逻辑关系看,门电路的输入端或输出端只有两种状态,无信号以“0”表示,有信号以“1”表示。也可以这样规定:低电平为“0”,高电平为“1”。门电路一般配合二级管制做。
1.2、与门
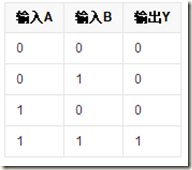
一种基本的门电路,有多个输入端,一个输出端。当所有的输入同时为高电平(逻辑1)时,输出才为高电平,否则输出为低电平(逻辑0)。
与门的真值表:
与门的二级管实现:
以二极管实现为例,与门的实现原理为:
如图:为二极管与门电路,Vcc = 5v,R1 = 3KΩ, 假设3v及以上代表高电平,0.7及以下代表低电平,
下面根据图中情况具体分析一下,
1. Ua=Ub=0v时,D1,D2正向偏置,两个二极管均会导通,此时Uo为电位为0.7v.,输出为低电平
2.当Ua,Ub一高一低时,不妨假设Ua = 3v,Ub = 0v,这时我们不妨先从D2开始分析,
D2会导通,导通后D2压降将会被限制在0.7v,那么D1由于右边是0.7v左边是3v所以会反向偏置而截止,因此最后Uo为0.7v低电平输出,这里也可以从D1开始分析,如果D1导通,那么Uo应当为3.7v,
此时D2将导通,那么D2导通,压降又会变回0.7,最终状态Uo仍然是0.7v.输出低电平,此时D1马上截止。
3. Va=Vb=3v,这个情况很好理解, D1,D2都会正偏,Uy被限定在3.7V.
总结(借用个定义):通常二极管导通之后,如果其阴极电位是不变的,那么就把它的阳极电位固定在比阴极高0.7V的电位上;如果其阳极电位是不变的,那么就把它的阴极电位固定在比阳极低0.7V的电位上,人们把导通后二极管的这种作用叫做钳位。(特别说明:压差大的二极管先导通,先钳位,先导通的二极管具有电路控制权)
1.3、或门
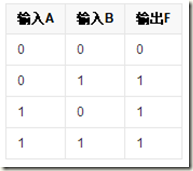
一种基本的门电路:或门有多个输入端,一个输出端,只要输入中有一个为高电平时(逻辑“1”),输出就为高电平(逻辑“1”);只有当所有的输入全为低电平(逻辑“0”)时,输出才为低电平(逻辑“0”)
或门的真值表:
或门的二级管实现:
如图,这里取Vss=0v,不取-10v
1、当Ua=Ub=0v时,D1,D2都截至,那么y点为0v.
2、当Ua=3v,Ub=0v时,此时D1导通,Uy=3-0.7=2.3v,D2则截至
同理Ua=0v,Ub=3v时,D2导通,D1截至,Uy=2.3v.
3、当Ua=Ub=3v时,此时D1,D2都导通,Uy=3-0.7=2.3v.
1.4、非门
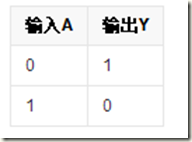
一种基本的门电路:非门有一个输入和一个输出端。当其输入端为高电平(逻辑1)时输出端为低电平(逻辑0),当其输入端为低电平时输出端为高电平。也就是说,输入端和输出端的电平状态总是反相的。
非门的真值表:
三级管非门的实现:
晶体管“非”门电路不同于放大电路,管子的工作状态或从截止转为饱和,或从饱和转为截止。“非”门电路只有一个输入端A,
当A为“1”(设其电位为3V)时,晶体管饱和,其集电极,即输出端Y为“0”(其电位在零伏附近);
当A为“0”时,晶体管截止,输出端Y为“1”(其电位近似等于)。所以“非”门电路也称为反相器。加负电源是为了使晶体管可靠截止。
图中,是“非”门的门电阻,其作用是通过它向输出端提供电压。T饱和,上产生很大的压降,使集电极电位几乎与发射极的电位相等;截止时,通过加到集电极上,使集电极电压等于。是输入电阻,通过它给T加正向偏置电流,即输入信号。是反偏电阻,通过它给T加反向偏置电流。这两个电阻配合得当,才可以使输入“1”时T饱和导通,输入“0”时T可靠截止。1.5、其他门电路
其他门电路如:与非门、或非门、异或门等都是以上三个基本门电路组合而来。
异或门:若两个输入的电平相异,则输出为高电平1;若两个输入的电平相同,则输出为低电平0。亦即,如果两个输入不同,则异或门输出高电平1。
2、加减乘除计算
2.1、加法运算
加法器:对于1位的二进制加法,相关的有五个的量:1,被加数A,2,被加数B,3,前一位的进位CIN,4,此位二数相加的和S,5,此位二数相加产生的进位COUT。前三个量为输入量,后两个量为输出量,五个量均为1位。
计算机的加法器都是以上面的逐位进位加法器优化而来,不再深入探索,有兴趣的可自行查找资料。
加法器原理就是用门电路实现二进制的相加运算。
2.2、减法运算
在计算机中,加法和减法其实是一种运算,原因在于计算机表示负数的方法。
计算机中的数据存储时都会转化成相应的二进制补码,补码有三个特性:
1、一个负整数(或原码)与其补数(或补码)相加,和为模。
2、对一个整数的补码再求补码,等于该整数自身。
3、补码的正零与负零表示方法相同。
模的定义:“模”是指一个计量系统的计数范围。如时钟等。计算机也可以看成一个计量机器,它也有一个计量范围,即都存在一个“模”。例如:
时钟的计量范围是0~11,模=12。表示n位的计算机计量范围是0~2^(n)-1,模=2^(n)。
“模”实质上是计量器产生“溢出”的量,它的值在计量器上表示不出来,计量器上只能表示出模的余数。任何有模的计量器,均可化减法为加法运算。
例如:假设当前时针指向10点,而准确时间是6点,调整时间可有以下两种拨法:一种是倒拨4小时,即:10-4=6;另一种是顺拨8小时:10+8=12+6=6
举例:
1、如计算机要计算8-3
2、存储8为:0000 1000 (正数的补码与原码相同)
3、存储-3为:1111 1101 (负数的补码为符号为定为1,其他位求反码后加1)
4、8-3 可直接用加法器做加法运算8 + (-3) 二进制可得:0000 0101 转化为十进制为:5
2.3、乘法运算
详细请看:https://www.cnblogs.com/sfzyk/p/7444061.html
我们计算两个数相乘时一般如下计算:
其实加法器也是模拟这样的过程,只不过是改为了二进制数而已。计算机通过加法器和适当的移位操作完成了乘法运算。
例子:
1011 X 1001 用十进制表示为 11X9 结果当然为99
以上文章中有很多乘法器的优化,我只讲我觉得好理解的一个
一、乘数寄存器四位保存1011。
二、被乘数寄存器四位保存1001。
三、乘积寄存器八位保存乘积,初始0000 0000,乘积寄存器只前四位参与运算,后四位只为记录。
1、第一次运算取乘数最后一位 得1,乘积寄存器前四位加 被乘数 得 1001 0000
2、乘数寄存器右移一位得:0101 乘积寄存器右移一位得 0100 1000
3、第二次运算重复步骤1、2 得,乘数:0010 乘积:0110 1100
4、如此,乘数有几位就重复次几运算,当乘数最后一位为0 时不做加操作,只进行移位。
5、第三次运算得,乘数:0001 乘积: 0011 0110
6、第四次运算得,乘数:0000,四次后整个运算完成,乘积:0110 0011 转化为十进制为:99
如上步骤中我们可以看出,计算机计算乘法跟我们计算乘法时的步骤一样,我们用乘数的个十百千们分别与被乘数相乘,然后错位相加得积,计算积也是把乘数的第一二三四位分别与被乘数相乘(相乘时乘数为1则积为被乘数,乘数为0时则四位全为0所以此时只进行移位操作) 然后用移位操作来模拟错位相加。
2.4、除法运算
详细请看:https://www.cnblogs.com/sfzyk/p/7444061.html
文章里也有很多除法器优化方案,我只以容易理解的说,其原理都是一般。
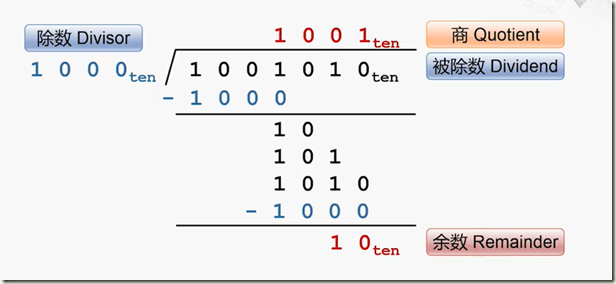
原理:除法可以变化为减法来算,一个数除以另一个数,可以理解为一个数循环减去另一个数减了几遍商便是几,这种方式在十进制里可能实在麻烦,但是在二进制里却简单了不少。
如果两个一位数相除8/3 可理解为8-3-3 = 2,得商为2 余数为2,但在二进制里两个一位数相除只有两种可能,一种是我大于你,商得1余数是两个数相减,另一种是我小于你商是0,余数是我本身;
如上计算方式我们十进制时也是常用的,只是我们配合九九乘法口决计算,而二进制里只需要从被除数高位开始逐位与除数相减,减的到此为得1 ,决不会有可以减两次的可能(即商不可能得2),减不到此位得0;
1、被除数十一位寄存,其实有效数字只占七位、除数四位寄存、商八位寄存,被除数参与运算的只有前四位(因为除数为四位即前四位)
2、被除数:0000 1001 010 除数:1000 商:0000 0000
3、参于运算的值我用红色标识: (1)被除数左移进入运算位后位补0: 0001 0010 100 除数:1000 减不到商得0 余为0001 商左移<1>为0000 0000
4、(2)被除数左移一位 变为:0010 0101 000 除数:1000 减不到此为得0 余为0010 商左移<2>为0000 0000
5、(3)被除数再左移变为:0100 1010 000 商左移<3>为0000 0000,(4)再左移得:1001 0100 000 此时可以减得 商左移<4>为0000 0001 余数为:0001,被除数被减后变为:0001 0100 000
6、(5)被除数左移变为0010 1000 000 <5>商左移为0000 0010 (6)再左移:0101 0000 000 <6>商左移为0000 0100 (7)再左移:1010 0000 000 此时可以减得 <7>商左移为0000 1001 余数为:0010 被除数被减后变为:0010 0000 000
7、被除数有几位就移动几位,商也跟着移动几位,如上图标号标识,七次移位后得商为:0000 1001 余数为:0010 后七位舍去,只要参与计算的前四位。转化为十进制为74/8 = 9 余 2
总结:除法器可以用减法替代除法,因为这样移位相减,在某一位上最多只能减一次被除数便会小于除数,所以商得1,同理十进制被除数和除数如此移位相减的话在某一位上最多只能减九次,即商最大只能为9。