POJ 1511 Invitation Cards

题面：

传送门

Invitation Cards

Input file: standard input

Output file: standard output

Time limit: 8 second

Memory limit: 256 megabytes

 

In the age of television, not many people attend theater performances. Antique Comedians of Malidinesia are aware of this fact. They want to propagate theater and, most of all, Antique Comedies. They have printed invitation cards with all the necessary information and with the programme. A lot of students were hired to distribute these invitations among the people. Each student volunteer has assigned exactly one bus stop and he or she stays there the whole day and gives invitation to people travelling by bus. A special course was taken where students learned how to influence people and what is the difference between influencing and robbery. 

The transport system is very special: all lines are unidirectional and connect exactly two stops. Buses leave the originating stop with passangers each half an hour. After reaching the destination stop they return empty to the originating stop, where they wait until the next full half an hour, e.g. X:00 or X:30, where 'X' denotes the hour. The fee for transport between two stops is given by special tables and is payable on the spot. The lines are planned in such a way, that each round trip (i.e. a journey starting and finishing at the same stop) passes through a Central Checkpoint Stop (CCS) where each passenger has to pass a thorough check including body scan. 

 

All the ACM student members leave the CCS each morning. Each volunteer is to move to one predetermined stop to invite passengers. There are as many volunteers as stops. At the end of the day, all students travel back to CCS. You are to write a computer program that helps ACM to minimize the amount of money to pay every day for the transport of their employees. 

 

Input

The input consists of N cases. The first line of the input contains only positive integer N. Then follow the cases. Each case begins with a line containing exactly two integers P and Q, 1 <= P,Q <= 1000000. P is the number of stops including CCS and Q the number of bus lines. Then there are Q lines, each describing one bus line. Each of the lines contains exactly three numbers - the originating stop, the destination stop and the price. The CCS is designated by number 1. Prices are positive integers the sum of which is smaller than 1000000000. You can also assume it is always possible to get from any stop to any other stop.

 

Output

For each case, print one line containing the minimum amount of money to be paid each day by ACM for the travel costs of its volunteers.

 

Example

Input

2

2 2

1 2 13

2 1 33

4 6

1 2 10

2 1 60

1 3 20

3 4 10

2 4 5

4 1 50

Output

46

210

 

题目描述：

ACM的成员要到不同的公交站发邀请函。每个成员从CCS（记录为公交站1）出发，分别到各个公交站（公交站有P个，CCS也算一个公交站），然后再从原来的公交站回到CSS。问所有ACM成员来回所需要的最小花费。（注：每次给出的“路线”都是单向的）

 

题目分析：

这题是双向最短路问题：我们可以把“花费”看成是路程，这样，问题就转化为：从源点 1 到点 x (2 <= x <= P) 的最短距离，加上点 x (2 <= x <= P) 到 源点 1 的最短距离。注意，这里给出的路线是单向的！！！所以我们要求两次最短路：

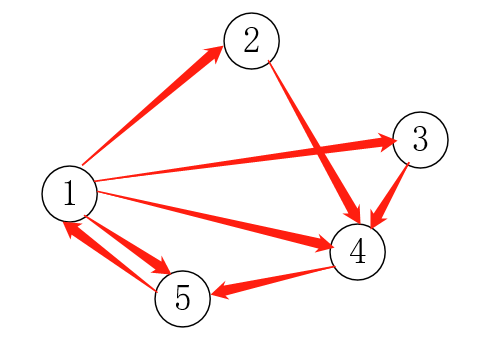
求两次最短路的原因：注意到这幅图：从1到2有一条直接的路径，但是从2返回到1要先从2到4，从4到5，从5才能返回到1.

 

从源点到各个点的距离当然容易求，直接应用最短路算法 (dijk或者spfa) 就行了，但是，如何求回去的最短距离？难道我们要对每个点应用最短路算法（就是把每个点都当成源点，然后分别计算出每个点到点1的最短路）？显然，这样做会超时。我们需要再想想：

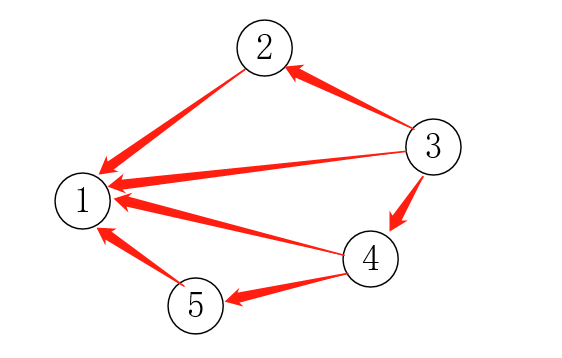
（注：为了方便，图中只标记了可以回去的路）

分析一下上面的图：假设我们已经知道3回到1花费最小的路径是：从3到2，再从2到1。那么，这条路径就是3回到1的“最短路”（废话(￣▽￣)" ）：

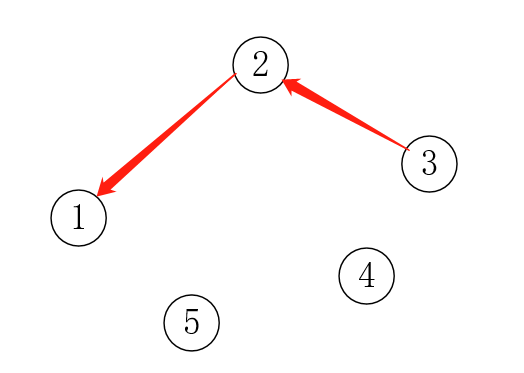
我们可不可以反过来思考：如何可以从1出发，找到3回到1的“最短路”。没错，答案就是边反过来：

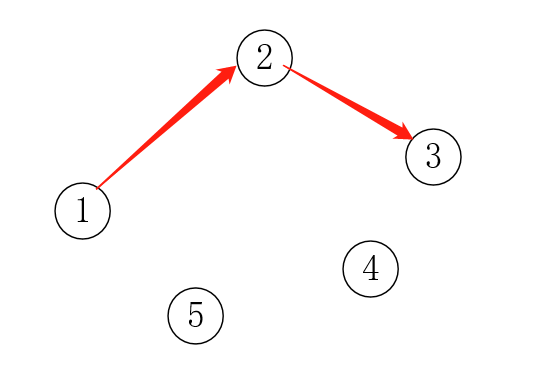
这样就能从1出发，应用最短路算法，找到3回到1的最短路了。对于其他点也是一样：只要把图的所有边反过来，就可以直接从1出发，找到其他点到点1的最短路：

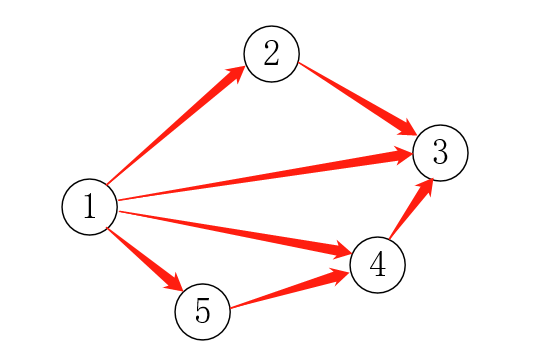
这样做只需要把1当成源点，应用一次最短路算法（这里要用 队列 / 优先队列 优化过的）就可以算出每个点回去的距离了。

 

对于这道题，存图不能用普通的邻接矩阵去存，因为开不了这么大的二维数组。这时我们就要用到“邻接表”去存图：邻接表有很多种实现方式，既可以用vector，也可以用数组模拟链表。总之，邻接表的核心：存的是一个点连接的所有“边”，“边”的属性一般有边的权值和“目的”点，示意图：

 

 

AC代码：

vector：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const int maxn = 1000000 + 5;
const int inf = 0x3f3f3f3f;
int n, m;
int dis[maxn];      //距离
int vis[maxn];      //标记数组

struct edge{
    int to, cost;
};
vector<edge> G[maxn];   //邻接表

struct cmp{
    bool operator () (int a, int b){
        return dis[a] > dis[b];       //优先级:距离小的优先级高
    }
};

int u[maxn], v[maxn], w[maxn];    //u:起点, v:终点, w:花费(距离，路程)

long long dijkstra(int st){

    priority_queue<int, vector<int>, cmp> q;   
 
    dis[st] = 0;      //源点到自己本身的距离
    int to, cost;     
    q.push(1);        //加入源点到优先队列

    while(!q.empty()){
        st = q.top(); q.pop();    //取出点
        if(vis[st]) continue;     //访问过就跳过
        vis[st] = 1;              //标记访问过

        for(int i = 0; i < G[st].size(); i++){
            to = G[st][i].to;
            cost = G[st][i].cost;
            
            if(dis[to] > dis[st]+cost){   
                dis[to] = dis[st]+cost;   //更新距离
                q.push(to);   //被更新过的点才会
            }
        }
    }

    long long ans = 0;  //距离之和
    for(int i = 1; i <= n; i++) ans += dis[i];
    
    return ans;
}

void add_edge(int u, int v, int w){
    edge temp;
    temp.to = v, temp.cost = w;
    G[u].push_back(temp);
}

void clear_G(){
    for(int i = 1; i <= n; i++) G[i].clear();
}

int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= m; i++){
            scanf("%d%d%d", &u[i], &v[i], &w[i]);
        }

        clear_G();  //清除图
        memset(dis, inf, sizeof(dis));
        memset(vis, 0, sizeof(vis));
        for(int i = 1; i <= m; i++){
            add_edge(u[i], v[i], w[i]);   //加入边
        }
        
        long long sum = 0;
        sum += dijkstra(1);  


        clear_G();
        memset(dis, inf, sizeof(dis));
        memset(vis, 0, sizeof(vis));
        for(int i = 1; i <= m; i++){
            add_edge(v[i], u[i], w[i]);
        }
        
        sum += dijkstra(1);
        printf("%lld
", sum);

    }
    return 0;
}

数组模拟链表：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn = 1e6+5;
const int inf = 0x3f3f3f3f;

int n;
int dis[maxn];
int vis[maxn];

int u[maxn], v[maxn], cost[maxn];   

int total;  //边的总数
int to[maxn], len[maxn], first[maxn], next[maxn];

void clear_edge(){
    memset(first, -1, sizeof(first));
    total = 0;
}

void add_edge(int u, int v, int cost){
    to[total] = v;
    len[total] = cost;
    
    //数组模拟链表
    next[total] = first[u];  //next存上一条边
    first[u] = total;        //first存第最后一条边
    
    total++;
}

struct cmp{
    bool operator () (int a, int b){
        return dis[a] > dis[b];
    }
};

long long dijkstra(){
    
    memset(dis, inf, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    dis[1] = 0;

    priority_queue<int, vector<int>, cmp> q;
    q.push(1);

    while(!q.empty()){
        int u = q.top(); q.pop();
        if(!vis[u]){
            vis[u] = 1;

            int To, Len;
            for(int e = first[u]; e != -1; e = next[e]){
                To = to[e];
                Len = len[e];
                if(dis[To] > dis[u]+Len){
                    dis[To] = dis[u]+Len;
                    q.push(To);
                }
            }
        }
    }

    long long ans = 0;
    for(int i = 1; i <= n; i++){
        ans += dis[i];
    }
    return ans;
}

int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        int m;
        scanf("%d%d", &n, &m);
        for(int i = 0; i < m; i++){
            scanf("%d %d %d", &u[i], &v[i], &cost[i]);
        }

        
        clear_edge();
        for(int i = 0; i < m; i++)
            add_edge(u[i], v[i], cost[i]);
        long long res = dijkstra();

        
        clear_edge();
        for(int i = 0; i < m; i++)
            add_edge(v[i], u[i], cost[i]);
        res += dijkstra();

        printf("%lld
", res);
    }
    return 0;
}