题面:
瞬间移动
Input file: standard input
Output file: standard output
Time limit: 2 second
Memory limit: 256 megabytes
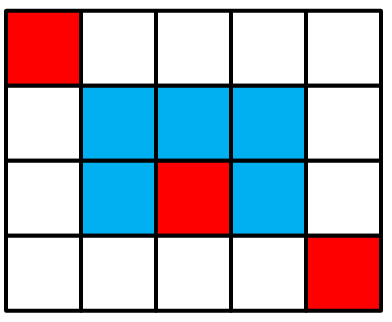
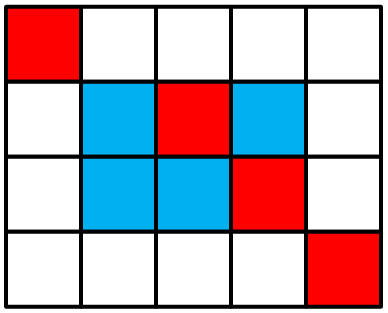
有一个无限大的矩形,初始时你在左上角(即第一行第一列),每次你都可以选择一个右下方格子,并瞬移过去(如从下图中的红色格子能直接瞬移到蓝色格子),求到第n行第m列的格子有几种方案,答案对1000000007取模。

Input
多组测试数据。
两个整数n,m(2≤n,m≤100000)
两个整数n,m(2≤n,m≤100000)
Output
一个整数表示答案
Example
Input
4 5
Output
10
题目描述:
无
题目分析:
这题用到的知识点:快速幂,组合数,逆元与费马小定理。我们先分析一下样例:从格子(1, 1)到格子(4, 5):
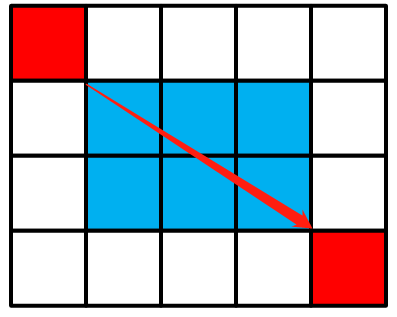
从这里我们可以看到,其中一种方案就是:直接到达终点。其次,我们想到的方案是通过中间一个格子来到达终点:
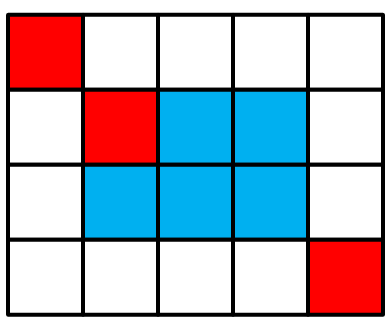
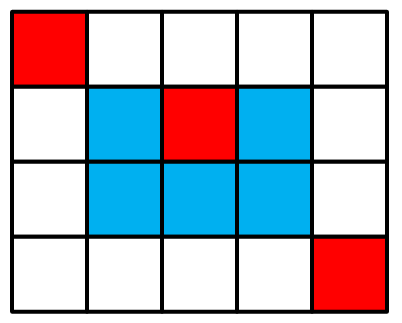
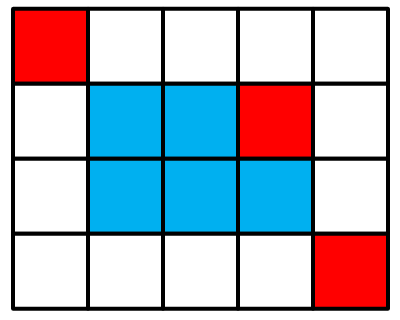

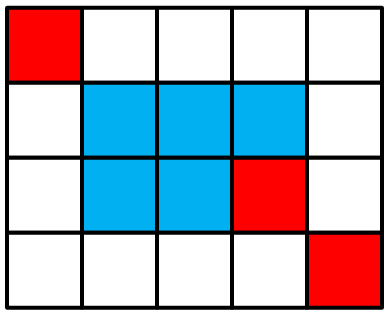
最后,我们可以选取中间两个格子来到达终点:
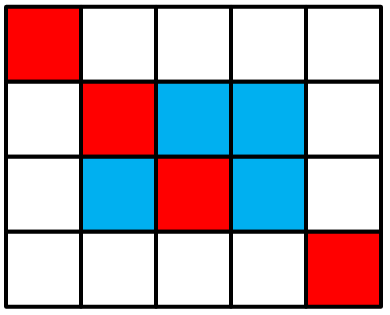
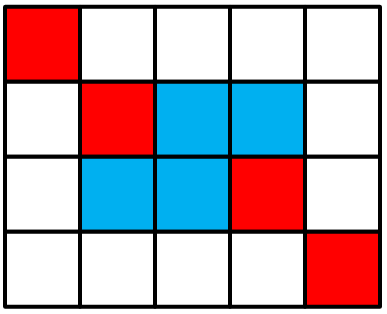
一共10种情况,这里我们是以中间选多少格子来分类讨论的:
中间不选格子:1种中间选1个格子:6种中间选2个格子:3种
那么,我们怎样计算出中间选x个格子有多少种情况?
我们先看中间选1个格子是怎样选出来的:
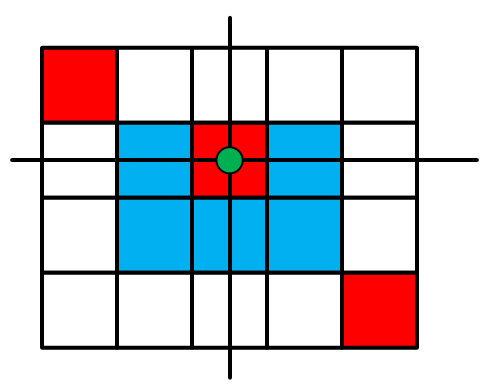
当我们确定了1行和1列的时候,就可以确定1个格子的位置。按照组合数学的知识,我们可以知道中间选一个格子的方案数为:C(2, 1)*C(3, 1),也就是6。
当我们中间选2个格子的时候:
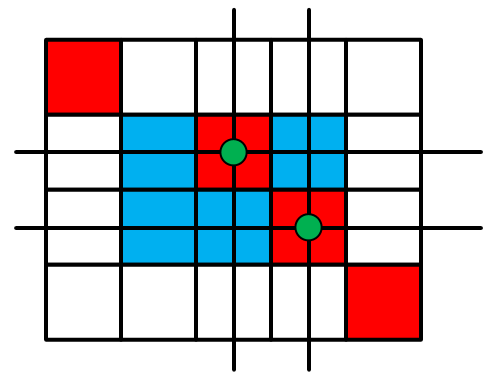
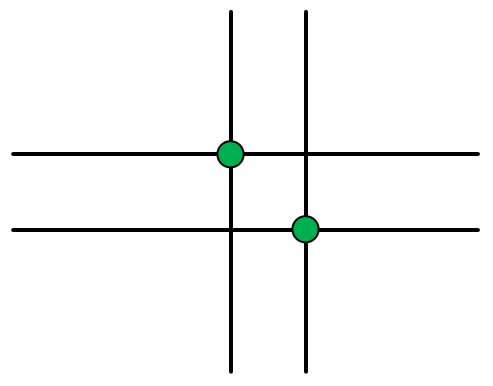
这时,我们确定了2行2列,因为每一次我们只能选右下方的格子,所以我们选择右下方对角线方向的直线的交点,这时2个格子的位置就被确定了。
方案数:C(2, 2)*C(3, 2),也就是3。
所以,到达格子(4, 5)的方案数就是:C(4-2, 0)*C(5-2, 0) + C(4-2, 1)*C(5-2, 1) + C(4-2, 2)*C(5-2, 2)。
如果是到达格子(5, 4),其实方案数也是一样的(对称关系),只要看成(4, 5)的情况就好了。
有的人可能有疑问:中间如果要选3个格子或以上怎么办?其实道理和上面一样,我就不多说直接上图吧:
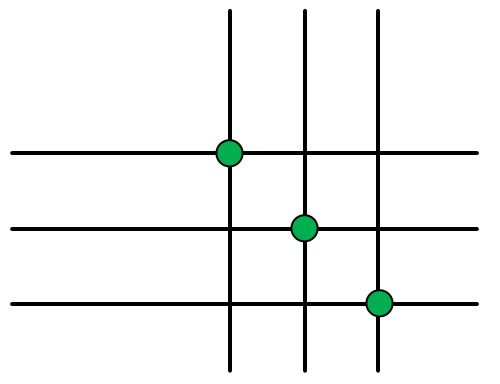
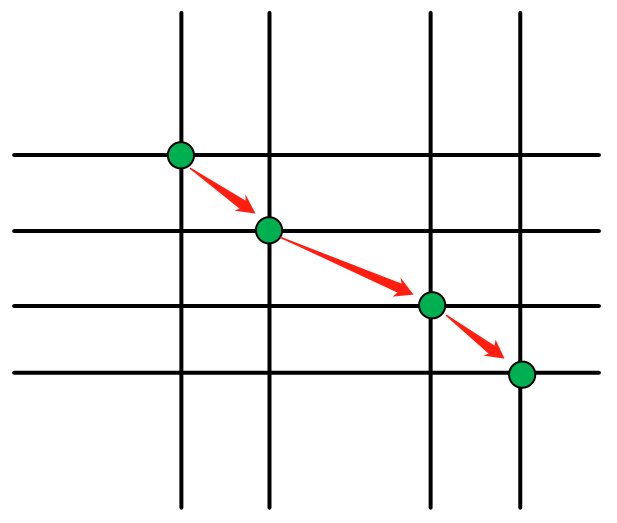
所以计算公式是:C(n-2, 0)*(m-2, 0) + C(n-2, 1)*(m-2, 1) + ...... + C(n-2, n-2)*C(m-2, n-2) (n <= m 时)
如果 n > m,直接交换 n,m 就行了。
这时,我们计算组合数C(a, b) = a! / ( b! * (a-b)! )。因为组合数太大,所以答案要求我们对组合数进行取模,也就是C(a, b) % p (p == 1000000007)。但是取模就涉及到一个问题:我们可以对含有乘法的运算进行边乘边取模,但是不能对含有除法的运算进行取模运算。举个例子:对于乘法来说,(6*3)%4 == (6%4)*3%4;但是对于除法来说,(6/3)%4 != (6%4) / (3%4) %4 (左侧结果是2,右侧结果是0)。为了把 / ( b! * (a-b)! ) 等效为一个乘法的运算,也就是除于一个数 x 取模的结果,等于乘于一个数 y 取模的结果,我们就要用到逆元的知识。逆元的作用就是:如果数 w,x,y,p符合这样的运算:w / x % p == w * y % p,那么y就是x的逆元。如果p是质数,那么根据费马小定理(这里就不推导了( ̄▽ ̄)"),这个 y == x p-2 。而这个 x p-2 怎么算?如果直接求速度太慢了,这时就要用到快速幂,把O(p-2)的时间复杂度降到O( log(p-2) )。最后,我们预处理一下数据就行了。记得要边乘边模才不会溢出(做完一次乘法就立刻取模,注:取模运算符的优先级和乘除法是一样的)
AC代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 const long long mod = 1000000007; 7 long long f[100005]; 8 long long inv[100005]; 9 10 long long quick_pow(long long base, long long x){ //快速幂 11 long long ans = 1; 12 while(x){ 13 if(x & 1) ans = ans*base%mod; 14 base = base*base%mod; 15 x >>= 1; 16 } 17 return ans%mod; 18 } 19 20 long long comb(int a, int b){ //组合数 21 return f[b]*inv[a]%mod*inv[b-a]%mod; 22 } 23 24 void fac(){ //预处理 25 f[0] = 1; 26 inv[0] = 1; 27 for(int i = 1; i <= 100005; i++){ 28 f[i] = f[i-1]*i%mod; //得出阶乘 29 } 30 for(int i = 100005; i > 0; i--){ 31 inv[i] = quick_pow(f[i], mod-2); //得出阶乘对应的逆元 32 } 33 } 34 35 int main(){ 36 int n, m; 37 fac(); 38 while(~scanf("%d%d", &n,&m)){ 39 if(n > m) swap(n, m); //交换n, m, 使小的在前,大的在后 40 n = n-2; 41 m = m-2; 42 long long ans = 0; 43 for(int i = 0; i <= n; i++){ 44 ans = (ans + comb(i, n)%mod*comb(i, m)%mod)%mod; //推导出的公式 45 } 46 cout << ans << endl; 47 } 48 return 0; 49 }